【EA电池SPM参数化】Matlab构建的简化单粒子SPM电化学模型，ESP，SP，包含测试数据，参数辨识代码以及验证的简化电化学模型P2D，锂离子电池，降阶电化学模型

         💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、SPM模型原理与Matlab实现

1. 模型核心方程与简化机制

2. Matlab实现步骤

二、测试数据获取与预处理

1. 数据来源与类型

2. 预处理流程

三、参数辨识算法与实现

1. 参数敏感度分类

2. 智能算法应用

四、ESP与SP模型对比及P2D验证

1. ESP vs. SP模型

2. P2D模型验证方法

五、创新研究方向

结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

一、SPM模型原理与Matlab实现

1. 模型核心方程与简化机制

• 基本原理：SPM将电极简化为单一球形粒子，忽略电解质浓度变化和三维扩散效应，仅基于固相扩散（Fick定律）和电化学反应（Butler-Volmer方程）描述电池行为。

  • 控制方程：

    

• 简化优势：计算效率高（较P2D模型快1000倍以上），适合实时BMS应用。

   

  

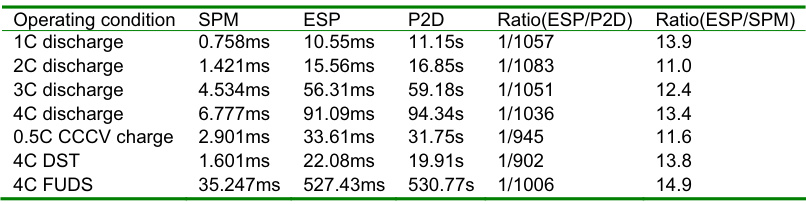
2. Matlab实现步骤

% 伪代码示例：SPM核心求解流程
% 1. 空间离散化（有限差分法）
N = 20; % 径向离散点数
dr = R_particle / (N-1); % 粒子半径等分
r = linspace(0, R_particle, N)';

% 2. 固相扩散方程离散化
A = gallery('tridiag', N, 1, -2, 1); % 三对角矩阵（中心差分）
A(1,1) = -3; A(1,2) = 3; % 边界条件（球心对称）
A(N,N) = -3; A(N,N-1) = 3; % 表面边界（电流密度关联）

% 3. Butler-Volmer方程求解（牛顿迭代法）
function eta = solveBV(j, c_s_surf)
    f = @(eta) j - i0*(exp(alpha_a*F/RT*eta) - exp(-alpha_c*F/RT*eta));
    eta = newtonRaphson(f, 0); % 初始猜测值0
end

% 4. 时间积分（ode45求解）
[t, C_s] = ode45(@(t,y) solidDiffusion(t,y,D_s,A), tspan, c_s_init);

关键实现技术：

• 有限差分法（FDM） ：将偏微分方程转化为常微分方程组，需处理边界条件（如球心对称性、表面电流关联）。
• 非线性求解：Butler-Volmer方程需迭代法（如牛顿法），初始值选择影响收敛性。
• OCV-SOC集成：通过实验数据拟合U_ocv = f(SOC)函数并查表调用。

---

二、测试数据获取与预处理

1. 数据来源与类型

数据类型	采集要求	用途
恒流充放电曲线	电流倍率0.1C–2C，记录间隔≤1s	OCV拟合、参数辨识
动态工况（DST/FUDS）	实车数据，采样间隔≤20s	模型动态响应验证
EIS阻抗谱	频率范围0.01Hz–10kHz	反应动力学参数辨识

2. 预处理流程

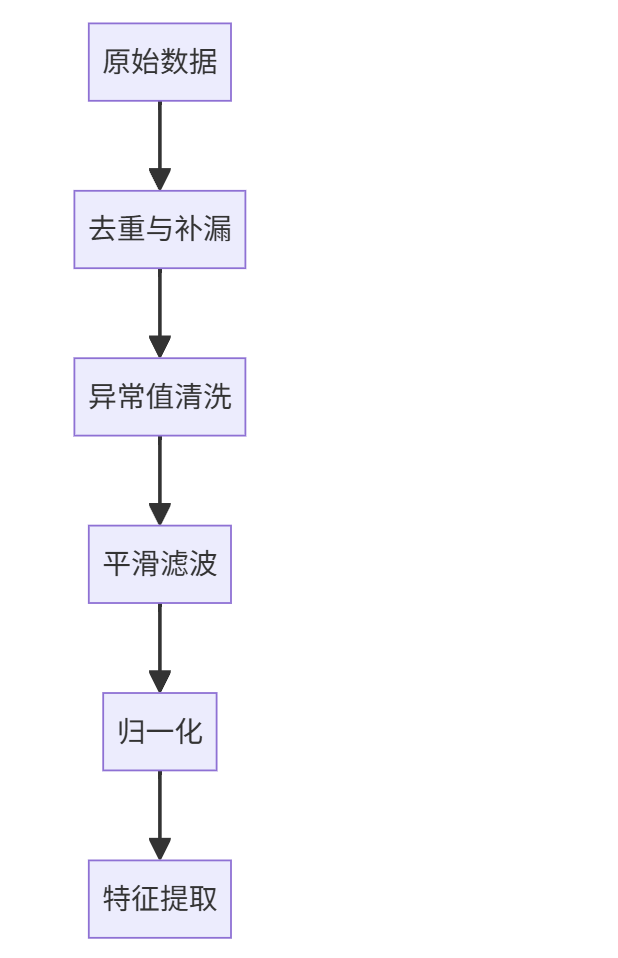
• 异常清洗：四分位法（IQR）剔除超限值，移动平均法平滑噪声。
• 归一化：Min-Max标准化（公式：x∗=x−xmin⁡xmax⁡−xmin⁡x∗=xmax​−xmin​x−xmin​​）。
• EIS处理：KK检验数据稳定性 → 删除非第一象限数据 → 韦伯阻抗段裁剪。

---

三、参数辨识算法与实现

1. 参数敏感度分类

参数类型	典型参数	辨识策略
高敏感度参数	DsDs​（扩散系数）、RΩRΩ​（内阻）	恒流工况+智能算法优先辨识
低敏感度参数	αa,αcαa​,αc​（传递系数）	动态工况辅助优化

2. 智能算法应用

• 多步辨识框架：
  1. 神经网络初估：用恒流数据训练LSTM网络输出高敏感参数初始值。
  2. 优化算法精调：
• 遗传算法/粒子群优化：最小化电压误差（目标函数：MSE=1N∑(Vsim−Vexp)2MSE=N1​∑(Vsim​−Vexp​)2）。
• 自适应差分进化：综合精度与效率最优（误差<3%）。
• 代码示例（PSO）：

  costFunc = @(params) simSPM(params, I_exp, V_exp); % 定义误差函数
  options = optimoptions('particleswarm', 'SwarmSize', 50, 'MaxIterations', 200);
  [optParams, MSE] = particleswarm(costFunc, nParams, lb, ub, options);
  

---

四、ESP与SP模型对比及P2D验证

1. ESP vs. SP模型

特性	SP模型	ESP模型（扩展单粒子）
电解质处理	忽略浓度变化	多项式近似电解质动力学
精度	低倍率（<1C）误差<5%	高倍率（2C）误差<50mV
计算复杂度	极低（约1ms/步）	中等（约10ms/步）
改进机制：ESP通过平均电流通量简化固液界面交换电流密度，保留电解质电势影响。

2. P2D模型验证方法

• 精度对比：在FUDS/DST工况下比较端电压RMSE（ESP平均RMSE<15mV vs. P2D）。
• 补偿优化：在LPM（集总粒子模型）中添加P2D的液相浓差过电压项，提升降阶模型精度。
• 计算效率：

  % P2D验证伪代码
  [V_p2d, \~] = solveP2D(I_input, params); % 全阶模型输出
  V_esp = solveESP(I_input, optParams);    % 降阶模型输出
  RMSE = sqrt(mean((V_p2d - V_esp).^2));  % 精度评估
  

---

五、创新研究方向

1. 物理信息神经进化：融合PINN与进化算法，直接嵌入Fick扩散定律约束，提升参数泛化性。
2. 实时降阶技术：POD（本征正交分解）对P2D模型进行模态截断，加速计算。

   

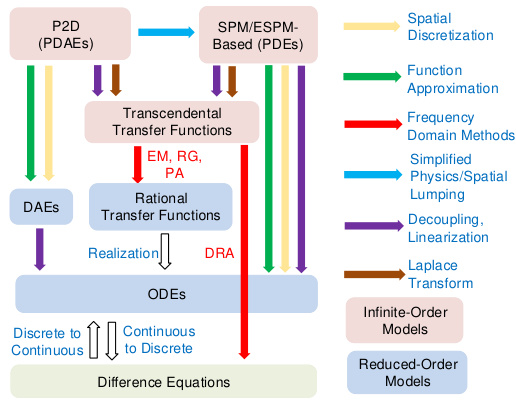
3. 老化耦合模型：引入SOH参数（如DsDs​衰减）至SPM，实现寿命预测。

---

结论

SPM模型通过Matlab实现的完整流程包括：

1. 模型构建：基于FDM离散固相扩散方程，牛顿法求解非线性反应项；
2. 数据驱动：严格预处理测试数据，结合智能算法多步辨识参数；
3. 验证优化：以P2D为基准验证ESP/SP精度，通过补偿项缩小误差；
4. 前沿扩展：融合PINN、POD等技术提升模型实用性与泛化能力。

此流程平衡精度与效率，为BMS设计提供可靠理论基础。建议优先采用ESP模型应对高倍率场景，并结合蜂群算法提升参数辨识效率。

📚2 运行结果

部分代码：

%% Electrochemical model parameter
% Load US18650VTC5A NCA cell parameter
run parameter/parameter.m

% Load measurement
load('US18650VTC5A_1C_20deg.mat');

% Calculate electrode capacities
[cn_low,cp_low] = init_SOC(p,0); % Calculate concentrations at 0% SOC
[cn_high,cp_high] = init_SOC(p,100);  % Calculate concentrations at 100% SOC
Delta_cn = cn_high-cn_low; % Calculate anode concentration difference
Delta_cp = cp_low-cp_high; % Calculate cathode concentration difference
qn = p.epsilon_s_n*p.Area*p.L_n*Delta_cn*p.Faraday/3600; % Calculate anode capacity
qp = p.epsilon_s_p*p.Area*p.L_p*Delta_cp*p.Faraday/3600; % Calculate cathode capacity

% Cell capacity deviation
Dataset.Q = 2.52; % Actual full cell capacity
Q_t = Dataset.Q/qn; % Calculate deviation to original parameterization
p.Q_n = p.Q_n*Q_t; % Scale anode capacity accordingly
p.Q_p = p.Q_p*Q_t;  % Scale cathode capacity accordingly
p.L_n = p.Q_n*3600/(p.epsilon_s_n*p.Area*p.c_s_n_max*p.Faraday); % Adjust anode thickness
p.L_p = p.Q_p*3600/(p.epsilon_s_p*p.Area*p.c_s_p_max*p.Faraday); % Adjust cathode thickness

% Interpolate data to seconds
Dataset.Time = Dataset.Time*3600; % Convert time to seconds
ip_t = 0:1:max(Dataset.Time); % Normalize time to 1s distance
Dataset.U = interp1(Dataset.Time, Dataset.U, ip_t); % Interpolate voltage
Dataset.I = interp1(Dataset.Time, Dataset.I, ip_t); % Interpolate current
Dataset.T2 = interp1(Dataset.Time, Dataset.T1, ip_t); % Interpolate measured temperature

% Parse data
t = ip_t; % Assign time as input
I =  Dataset.I; % Assign current as input
T2 = Dataset.T2; % Assing temperature as input

%% Input Data structure with time, current and temperature
% Current | Positive = Charge | Negative = Discharge
data.time = t;          % [s]
data.cur = I;           % [A]
data.T2 = T2+273.15;    % [K]

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1] Morozovska A N , Eliseev E A , Bravina S L ,et al.Strain-voltage and current-voltage Scanning Probe Microscopy (SPM) response of ionic semiconductor thin films: probing of deformation potential[J].Physics, 2012.DOI:10.48550/arXiv.1008.2389.

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取

                                                           ​