💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
在通信领域,数字仿真对于研究和优化各种通信系统具有重要意义。 预失真(DPD)算法是一种用于改善通信系统性能的关键技术。在无线通信中,功率放大器通常会引入非线性失真,这可能导致信号质量下降、频谱扩展以及干扰增加等问题。DPD 算法通过对输入信号进行预失真处理,使得经过功率放大器后的输出信号尽可能接近理想的线性放大状态,从而提高信号质量、降低误码率并提高系统的频谱效率。 透明多载波卫星链路是一种卫星通信链路,具有透明转发的特点,即卫星仅对接收的信号进行放大和转发,而不进行复杂的信号处理。多载波技术可以提高卫星链路的传输容量和频谱效率,适应高速数据传输的需求。在透明多载波卫星链路中,DPD 算法可以有效地补偿卫星转发器中的功率放大器非线性失真,提高链路的性能和可靠性。 通过数字仿真,可以对透明多载波卫星链路中的 DPD 算法进行深入研究和优化。可以模拟不同的信号条件、功率放大器特性以及链路参数,评估 DPD 算法的性能表现,如失真补偿效果、误码率性能、频谱效率等。数字仿真还可以帮助设计和调整 DPD 算法的参数,以适应不同的应用场景和系统要求。 总之,数字仿真、预失真算法和透明多载波卫星链路的结合为卫星通信系统的性能提升和优化提供了有力的工具和方法。
一、DPD算法基本原理与卫星通信适配性
1. 核心原理
DPD通过在功率放大器(PA)前插入非线性预失真模块,使预失真特性与PA的压缩特性互补,实现级联线性化。数学本质是构建PA的逆模型:
- 数学模型:基于Volterra级数或广义记忆多项式(GMP)描述非线性系统,考虑记忆效应(当前输入与历史输入的相关性)。
- 实现流程:

2. 卫星通信适配性
透明多载波卫星链路需同时处理多个载波信号,PA非线性导致:
- 互调失真(IMD) :多载波叠加引发频谱再生;
- AM/AM与AM/PM效应:信号幅度与相位非线性畸变。
DPD通过以下特性适配卫星场景: - 宽频带处理能力:抑制相邻信道干扰(ACI),支持>100MHz带宽;
- 记忆效应补偿:GMP模型可建模长时延记忆(如热效应引起的非线性变化)。
二、透明多载波卫星链路特性与DPD需求
1. 透明转发架构
-
技术定义:卫星仅进行射频处理(频率转换/放大/波束成形),不解析信号内容。
-
优缺点:
优点 缺点 低成本、易部署 长时延(单跳500ms+) 兼容现有卫星 需大量信关站 支持多运营商波束落地 PA非线性影响更显著
2. 多载波技术挑战
- 高峰均比(PAPR) :多载波叠加导致信号动态范围扩大,PA工作点易进入饱和区;
- 频谱效率与失真权衡:高阶调制(如32APSK)对非线性敏感,需DPD保障误码率。
三、DPD在卫星链路的实现方案
1. 算法选择与优化
- MIMO符号速率DPD(SRS-DPD):
- 在多载波场景下,以符号速率(非采样速率)处理信号,降低计算复杂度;
- 实验表明:在相同OBO(输出回退)下,EVM改善>5dB。
- 模型简化技术:
- 使用LASSO算法筛选Volterra级数关键项,减少参数数量;
- 查找表(LUT)替代实时计算,适应星载FPGA资源限制。
2. 反馈环路设计
-
间接学习架构:
- 长时延补偿:在反馈路径加入时延对齐模块,匹配星地传输延迟。
3. 性能验证(北斗案例)
DPD在北斗B2信号(ACE-BOC调制)中实现:
- 带外泄露抑制20dB;
- 相关损耗从0.7dB降至0.009dB。
四、数字仿真的关键技术作用
1. 仿真流程设计
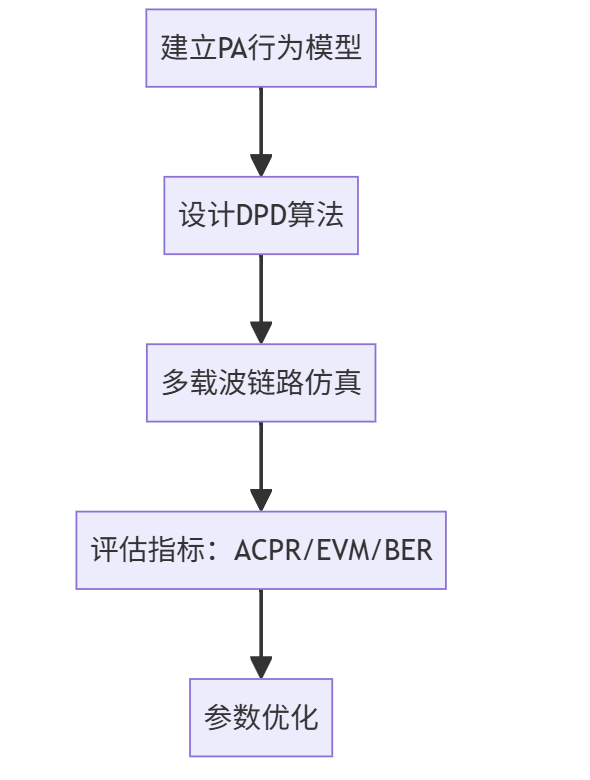
- PA建模:基于实测数据拟合Saleh模型或GMP系数;
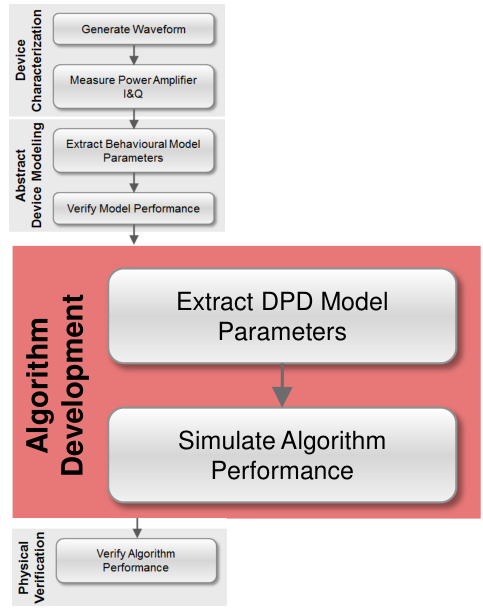
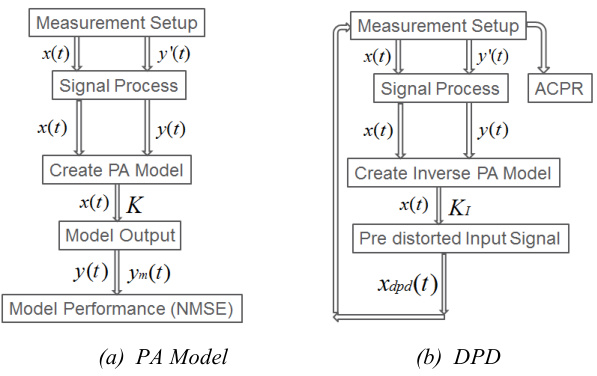
- 信道模拟:加入多普勒频移、雨衰等卫星信道特性。
2. 典型仿真工具与案例
- MATLAB/Simulink:
- 实现DVB-S2标准的三载波DPD仿真,支持32APSK调制与LDPC编码;
- 输出指标:信号干扰比(SIR)、星座图、误码率曲面。
- 数字孪生平台:
- 世冠科技“数字卫星系统”实现轨道操控预演与在轨故障推演;
- 北邮Satlink工具支持6G星地协议栈参数优化。
3. 优化方向
- 联合仿真:将电磁仿真(如HFSS)与通信系统仿真耦合,提升PA模型精度;
- 机器学习增强:利用RL优化DPD系数更新策略,适应动态负载。
五、技术挑战与未来方向
- 星上处理限制:
- FPGA资源制约模型复杂度,需开发低功耗DPD IP核;
- 热管理不足加剧PA记忆效应,需联合温度传感器动态调整模型。
- 多星协同:
- 透明架构不支持星间链路,限制DPD的分布式优化;
- 再生式载荷或成趋势,支持星上DPD预处理。
- 6G集成场景:
- 太赫兹频段PA非线性更显著,需宽频带DPD;
- 与智能反射面(RIS)联合优化,降低功放负担。
结论
数字仿真与DPD算法的结合为透明多载波卫星链路提供了“设计-验证-优化”闭环:
- 算法层面:SRS-DPD和GMP模型显著提升多载波线性度,支持高阶调制;
- 仿真层面:MATLAB/数字孪生实现全链路性能预演,降低实星测试成本;
- 系统层面:需突破星上处理瓶颈,向再生式载荷与AI协同演进。
📚2 运行结果

主函数部分代码:
clear all; close all; clc
tic
%% settings
Mod = 32; % APSK modulation for all carriers
Rate = 9/10; % LDPC code rate for all carriers
Es_NodB = 25; % Es/No in dB for the DPD identification
IBO = 6; % input back off the of HPA
Nsamp = 3800; % # of symbols for the DPD identification
% DPD settings
% DPD scheme (set DPD_type): NO DPD = 'No'
% memory polynomial MP data DPD = 'MP'
% reduced data MP DPD = 'RMP'
% SRS DPD = 'SRS'
% mem polynomial(reduced complex.) SRS = 'RSRS'
DPD_type = 'RSRS';
Pn = 3; % nonlinear order
Mn = [5 1 0]; % memory depths [linear third fifth ...]
%% 3 carrier base-band symbols
Nbits = 64800; % a frame in DVB-S2
nsymbols = Nbits/log2(Mod);
spc_eff = 4; %Changing this affects the magnitude of each circle
c = APSK_Const_Gen(Mod, spc_eff); % gray coded APSK Constellation
c = c/std(c);
modObj = modem.genqammod('Constellation',c, 'InputType', 'Bit') ;
for kk = 1:3 % 3 carriers
codeword = randi([0 1],1,Nbits);
AT(:,kk) = modulate(modObj, codeword'); % symbols of each carrier
end
%% Satellite link : pulse-shape IMUX TWTA OMUX pulse-shape sampling
[rd1 rd2 rd3 OBO] = MC_Core_channel(IBO,inf,AT(:,1),AT(:,2),AT(:,3));
rec = [rd1 rd2 rd3];
fprintf('\n ---- NO DPD --- \n')
fprintf('OBO no DPD : %1.2f \n',OBO)
% optimal scaling of each carrier
P1 = rd1\AT(:,1); P2 = rd2\AT(:,2); P3 = rd3\AT(:,3);
recn = [rd1.*P1 rd2.*P2 rd3.*P3];🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]Pu H J ,Hua N ,Chen Y , et al. Modelling and numerical simulation of heat transfer and hydrodynamic performance of multi-pass parallel flow condensers – A novel algebraic method to determine flow distribution[J]. International Communications in Heat and Mass Transfer,2024,159(PA).
[2]Cao Y ,Dai Z ,Zhang C , et al. Integrated experiments and numerical simulations for chromium (VI) surface complexation in natural unconsolidated sediments[J]. Applied Geochemistry,2024,173.
🌈4 Matlab代码实现





















 596
596

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








