1015 Reversible Primes (20 分)

1015 Reversible Primes (20 分)

A reversible prime in any number system is a prime whose “reverse” in that number system is also a prime. For example in the decimal system 73 is a reversible prime because its reverse 37 is also a prime.
Now given any two positive integers N (<10^​5​​ ) and D (1<D≤10), you are supposed to tell if N is a reversible prime with radix D.

Input Specification:

The input file consists of several test cases. Each case occupies a line which contains two integers N and D. The input is finished by a negative N.

Output Specification:

For each test case, print in one line if YesN is a reversible prime with radix D, or if not.No

Sample Input:

73 10
23 2
23 10
-2

Sample Output:

Yes
Yes
No

真的，题目看不懂就很难受。

百度翻译和右键翻译了都看不懂。。。

只能找大佬的文章看看啥意思。（英语关键啊

大概就是这个意思：

给出一个正整数N和D 如果N是素数 且 N的D进制 逆序 再转回十进制 也是素数 那么就输出Yes 否则No

嗯。然后上才艺~

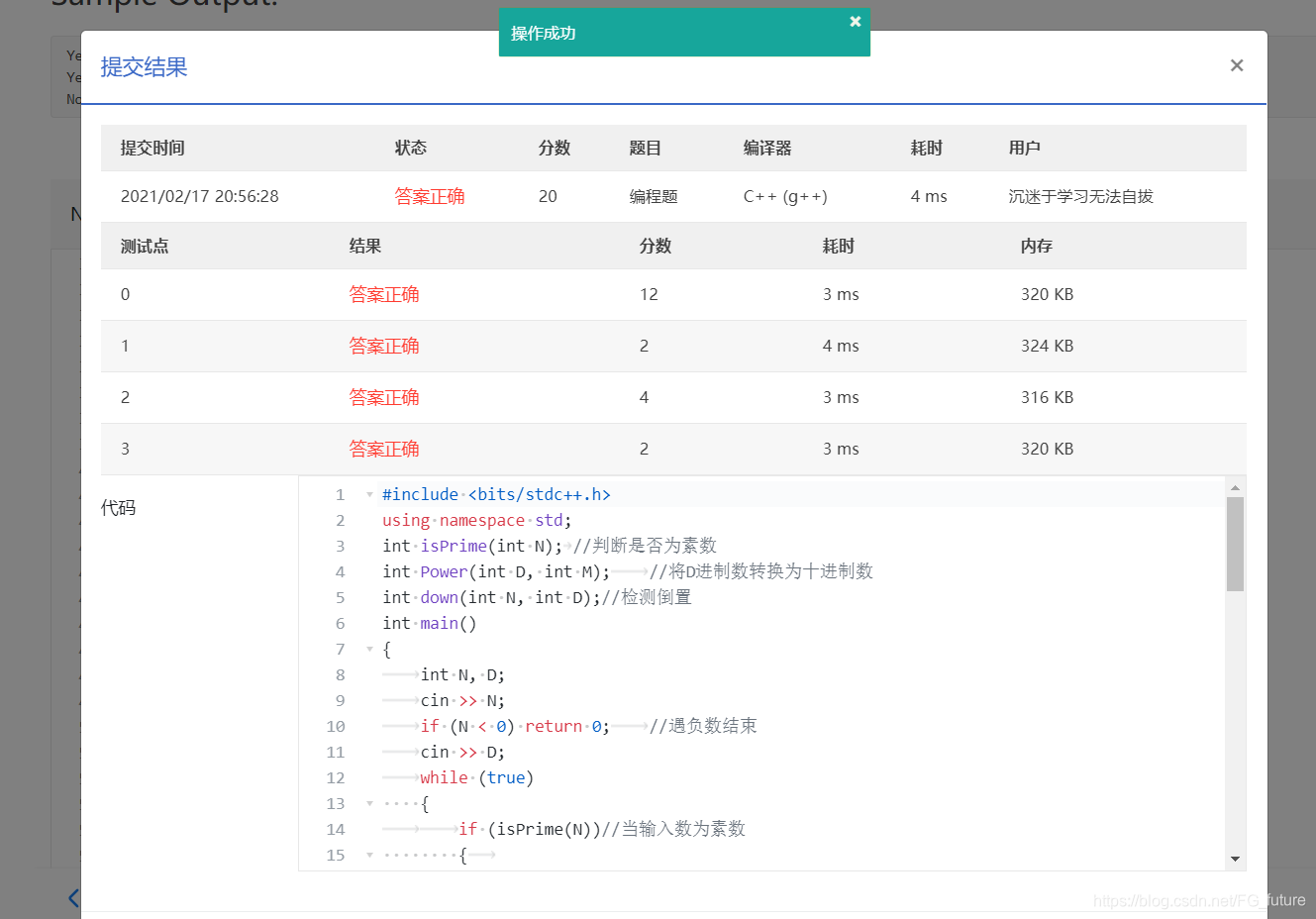
#include <bits/stdc++.h>
using namespace std;
int isPrime(int N);	//判断是否为素数
int Power(int D, int M);	//将D进制数转换为十进制数
int down(int N, int D);//检测倒置
int main()
{
	int N, D;
	cin >> N;
	if (N < 0) return 0;	//遇负数结束
	cin >> D;
	while (true)
    {
		if (isPrime(N))//当输入数为素数
        {	
			if (down(N, D))//判断D进制倒置数是否为素数
            {
                cout << "Yes" << endl;	//如果输入数D进制的倒置数仍为素数
            }
			else cout << "No" << endl;
		}
		else cout << "No" << endl;
		cin >> N;
		if (N < 0) return 0;	//遇负数结束
		cin >> D;
	}
	return 0;
}
int isPrime(int N)//判断是否为素数
{
	if (N == 1) return 0;
	for (int i = 2; i <= sqrt(N); i++)
		if (N%i == 0)
        {
            return 0;
        }
	return 1;
}
int Power(int D, int M) {
	int p = 1;
	for (int i = 0; i < M; i++) p *= D;
	return p;
}
int down(int N, int D)
{
	int p = 0, ret = 0;
	int downD[10001] = {0};
	while (N > 0)	//实现D进制倒置数的各位存储
    {
        downD[p++] = N % D; N /= D;
    }
	for (int i = p - 1; i >= 0; i--)
		ret += downD[i] * Power(D, p - i - 1);	//得到D进制倒置数
	int Judge;
	Judge = isPrime(ret);	//判断D进制倒置数是否为素数
	return Judge;
}