1019 General Palindromic Number (20 分)

最新推荐文章于 2025-12-27 16:49:17 发布

原创最新推荐文章于 2025-12-27 16:49:17 发布 · 103 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

PAT 专栏收录该内容

14 篇文章

订阅专栏

该博客主要介绍如何判断一个整数在给定的进制下是否为回文数。通过提供一个C++程序，博主展示了如何将整数转换为指定进制表示，并检查其是否为回文。程序通过比较数字的前半部分和后半部分来确定其是否为回文。

1019 General Palindromic Number (20 分)

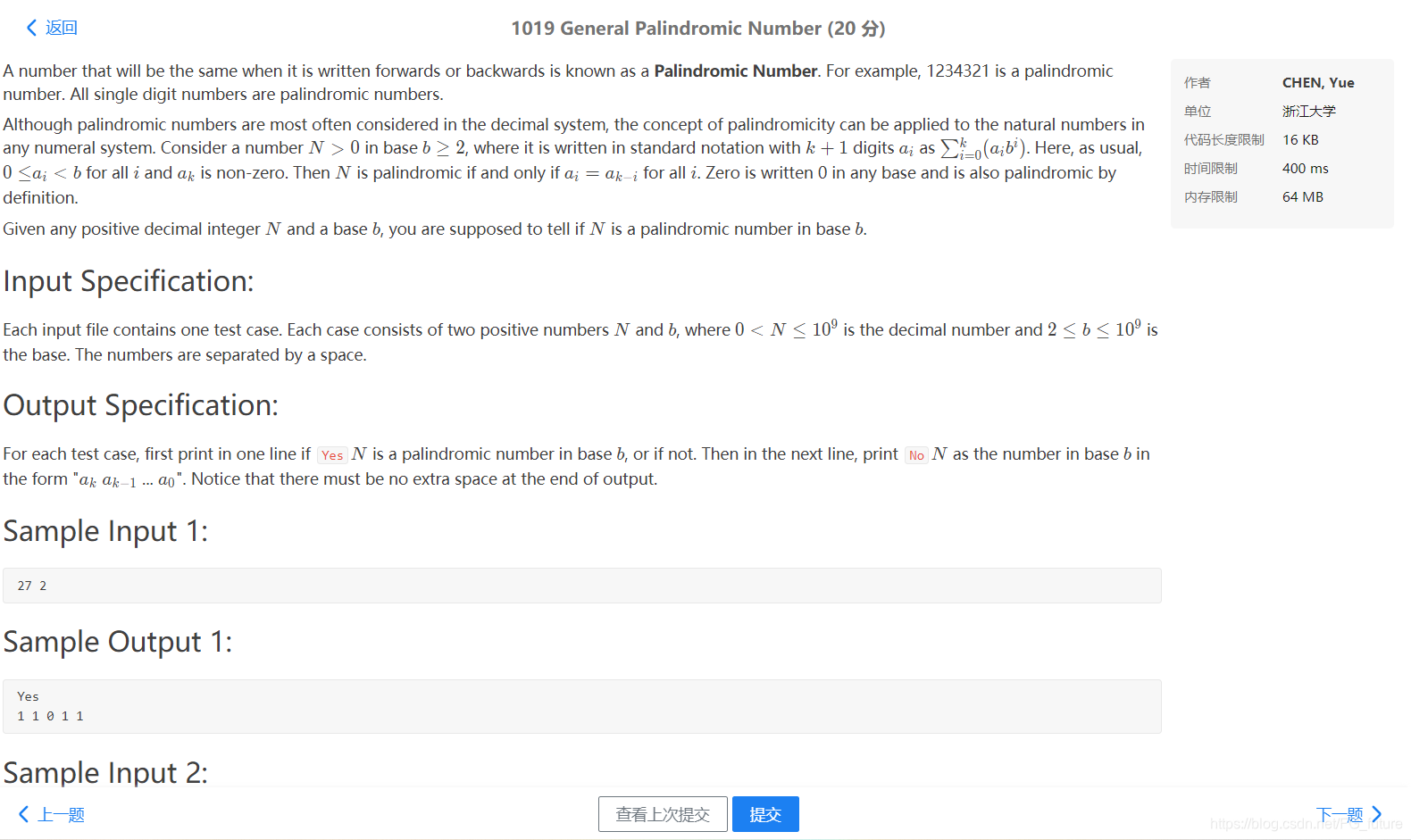
A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are palindromic numbers.

就给你们看看吧，不给你们写了。

啥意思呢，就是一个数如果类似于1234321这种，就叫做回文数。

给你两个数N，b。

N用b进制表示是不是回文数。

#include <bits/stdc++.h>
using namespace std;
int judge(int z[], int num)//判断是否为回文数
{
  for(int i = 0; i <= num / 2; i++)
  {
    if(z[i] != z[num - 1 - i])      return false;
  }
  return true;
}
int main()
{
    int n, b, z[40], num = 0;
    scanf("%d%d", &n, &b);
    do{
        z[num++] = n % b; 
        n /= b;
    }while(n != 0);
    int flag = judge(z, num);
    if(flag == true)
    {
        printf("Yes\n");
    }
    else
    {
        printf("No\n");
    }
    for(int i = num - 1; i >= 0; i--)
    {
        printf("%d", z[i]);
        if(i != 0)
        {
            printf(" ");
        }
  }
  return 0;
}