HNU算法分析与设计实验一（安全专业）

原创已于 2025-12-06 22:41:05 修改 · 844 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #学习笔记 #经验分享

于 2025-12-06 22:37:04 首次发布

2-11 整数因子分解问题

问题描述

大于1的正整数n可以分解为。例如：当n=12时，有8钟不同的分解式：

12=12 12=3×2×2

12=6×2 12=2×6

12=4×3 12=2×3×2

12=3×4 12=2×2×3

算法设计

对于给定的正整数n，计算n共有多少种不同的分解式

数据输入

由文件input.txt给出输入数据。第1行有1个正整数n（1≤n≤2,000,000,000）。

结果输出

将计算出的不同分解式数输出到文件output.txt。

输入文件实例输出文件实例

input.txt output.txt

12 8

算法实现与思路分析

直接递归

核心思路

对于f（n），当n == 1时直接返回0；否则定义一个total用来累加分解式数量，具体如下：对数进行遍历从2到n，如果能找到一个d被n整除，那么就累加上f（n/d）

递归式如下：

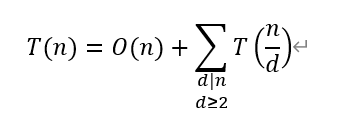
核心代码

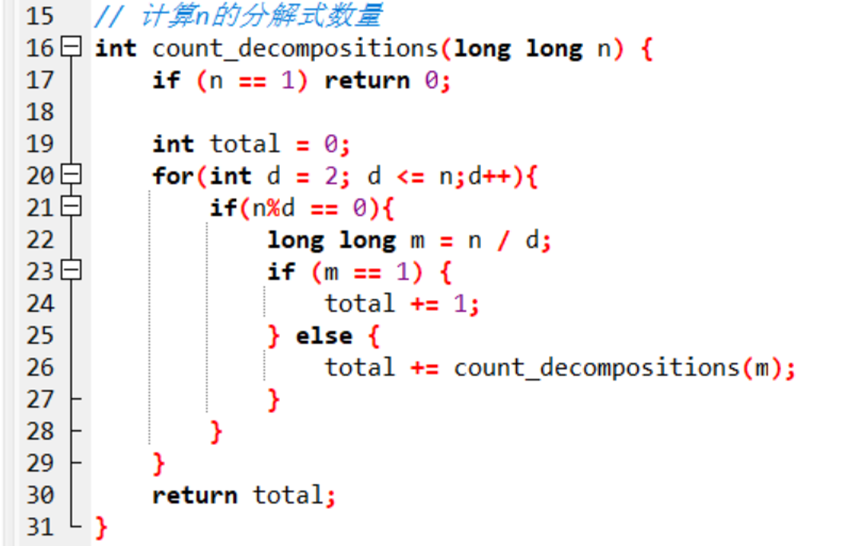
如下图代码所示：

定义一个total记录累加值，每次从2到n遍历寻找n的因数，之后进行递归调用f（n/d）

性能分析

可以使用数学归纳法证明其时间复杂度是O(n)：

空间复杂度为递归调用栈的深度O(logn)

初步优化的算法

核心思路

质因数分解：将n拆解为质因数幂的乘积形式（如12=2²×3），为生成所有因子奠定基础；
因子生成：基于质因数的指数组合，生成n的所有因子（如12的因子为1,2,3,4,6,12）；
递归计数：通过记忆化递归，对每个因子d≥2，累加以d为第一个因子的分解式数量，用缓存memo[n]存储已计算的f(n)，避免重复计算。

设f（n）表示n的所有分解式数量，f（n/d）表示以d为第一个因子的分解式数量，则有：

例如示例：

n=12时，因子d=2,3,4,6,12（还有1）

则：f(12)=f(6)+f(4)+f(3)+f(2)+1

核心代码

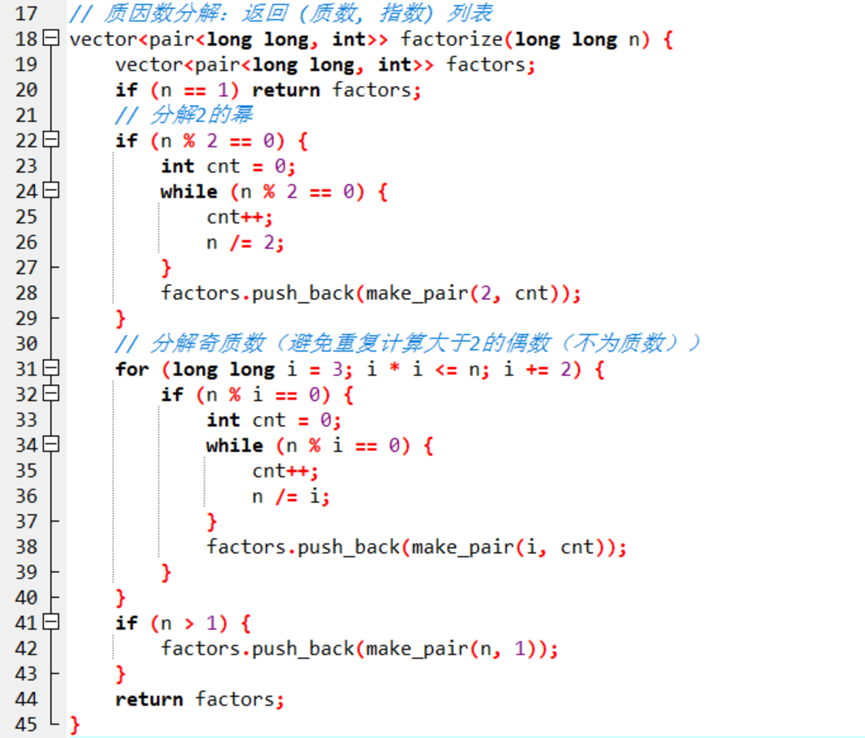
该部分是质因数分解的部分，对于每一个质因数，都除到底，使用cnt计算，即得到对应的幂，最终分解为的形式，并存储在二维数组中

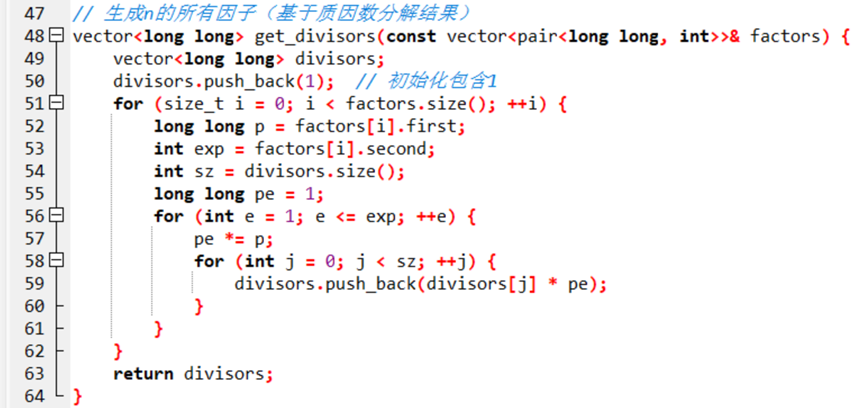
该部分得到n的所有因子，如质因数分解得到12=2²×3，那么可以得到因子还有4，6，12。

注意初始化包含1，后续对于每一个质因数p代表其底数，exp代表其幂

对已经得到的因数遍历乘上其他质因数的各个幂得到所有因数

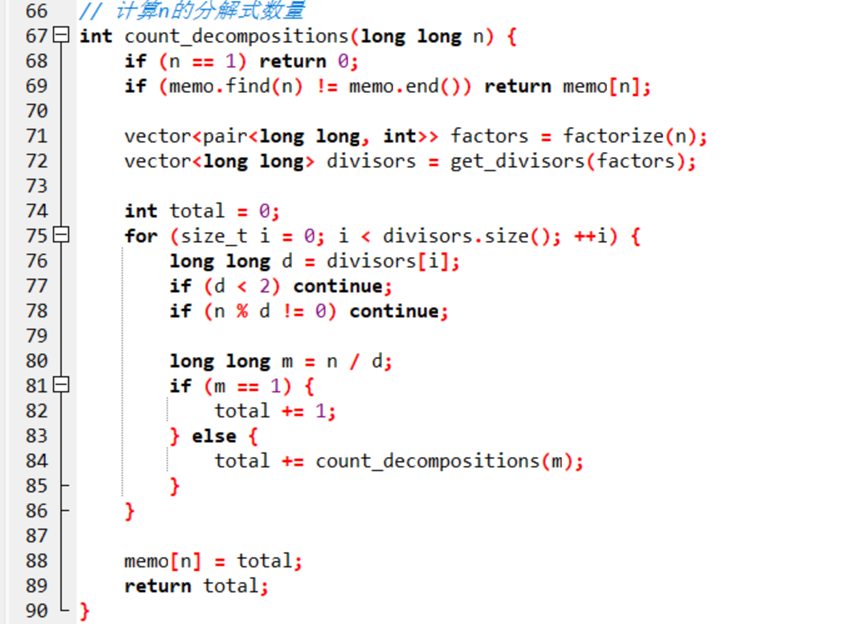
这部分通过统计以每一个因子作为第一个因子得到的分解式数量，最终累加得到结果

通过质因数分解和生成所有因子，开始遍历因子，如果n/d=1则+1即可，否则递归调用加上count_decompositions(n/d)

性能分析

测试（可以对比分析两种方法）

边界测试：1此时得到答案0，说明边界测试也能通过
小质数测试：13
幂测试：2的10次方=1024
大质数：1999999817（差距很明显）
大幂次：1073741824（2的30次幂）（差距非常大）
有大质数因子：102998249

总结

对两种算法进行对比

对比维度	直接递归算法	初步优化算法（质因数分解 + 记忆化）
时间复杂度	O(n)	最优O( $(\log n)^{c}$ )，最差O( $\sqrt{n}$ )
空间复杂度	O(logn)（仅递归栈）	O(logn)（递归栈 + memo + 因子存储）
核心缺陷	1. 重复计算多（如计算 f (12) 时多次调用 f (6)、f (2)） 2. 遍历范围大（从 2 到 n 找因子，效率低）	1. 需额外执行质因数分解步骤 2. 因子生成需处理质因数指数组合，逻辑稍复杂
适用场景	仅适用于 n 较小（如 n≤1000）的情况	适用于 n 较大（如 n≤2×10⁹）的场景，符合题目数据范围，且各种情况较稳定
执行效率（面对大数）	耗时久，易超时	耗时极短，可瞬间出结果