P5117 [USACO18DEC] The Bucket List B

题目描述

Farmer John 正在考虑改变他给奶牛挤奶的时候分配牛奶桶的方式。他认为这最终能使得他使用数量更少的桶，然而他不清楚具体是多少。请帮助他！

Farmer John 有 N 头奶牛（1≤N≤100），方便起见编号为 1…N。 第 i 头奶牛需要从时间 si​ 到时间 ti​ 之间挤奶，并且挤奶过程中需要用到 bi​ 个桶。于是多头奶牛可能在同一时刻都在挤奶；如果这样，他们不能使用相同的桶。也就是说，一个在第 i 头奶牛挤奶时用的桶不可以被任何在时间 si​ 到时间 ti​ 之间挤奶的其他奶牛使用。当然，这个桶在这段时间之外可以被其他奶牛所使用。为了简化他的工作，FJ 保证在任一时刻，至多只有一头奶牛开始或是结束挤奶（也就是说，所有的 si​ 和 ti​ 各不相同）。

FJ 有一个储藏室，里面有依次编号为 1、2、3、……的桶。在他的挤奶策略中，当某一头奶牛（比如说，奶牛 i）开始挤奶（在时间 si​），FJ 就跑到储藏室取出编号最小的 bi​ 个桶分配给第i头奶牛用来挤奶。

请求出 FJ 需要在储藏室中存放多少个桶才能使得他能够顺利地给所有奶牛挤奶。

输入格式

输入的第一行包含 N。以下 N 行，每行描述了一头奶牛，包含三个空格分隔的数 si​，ti​，和 bi​。 其中 si​ 和 ti​ 均为 1…1000 之间的整数，bi​ 为 1…10 之间的整数。

输出格式

输出一个整数，为 FJ 需要的桶的数量。

输入输出样例

输入 #1复制

3
4 10 1
8 13 3
2 6 2

输出 #1复制

4

说明/提示

在这个例子中，FJ 需要 4 个桶：他用桶 1 和桶 2 来给奶牛 3 挤奶（从时间 2 开始）。他用桶 3 给奶牛 1 挤奶（从时间 4 开始）。当奶牛 2 在时间 8 开始挤奶时，桶 1 和桶 2 可以再次利用，然而桶 3 不可以，所以他会使用桶 1、桶 2 和桶 4。

题目翻译：简单来讲，这道题就是求在1~1000的时间内，哪个时间点存在的桶的数量最多

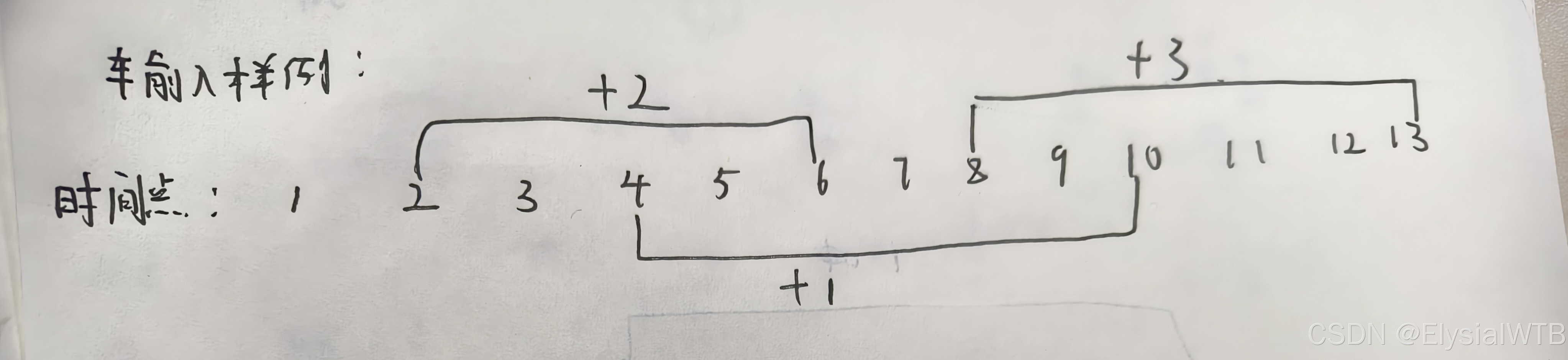
可以看出，在8，9，10这三个时间点存在的桶是最多的，那最多用到的桶就是4个。很明显，某个区间加一个数的形式。再求整个区间中最大的数字，用差分来算。

代码如下：

#include <bits/stdc++.h>

using namespace std;

int diff[1005] = {0};	//数组大小要看时间长短，不是奶牛数 

void chafen(int &s, int &t, int &b)	//差分算法 
{
	diff[s] += b;
	diff[t + 1] -= b;
}



int main()
{
	int n;
	cin >> n;
	int max_index = -1; //记录输入数据中最长的时间是哪个 
	while(n--)
	{
		int s, t, b;
		cin >> s >> t >> b;
		max_index = max(max_index, max(s, t));
		chafen(s, t, b);
	}
	
	for (int i = 1; i <= max_index; i++) {
		diff[i] += diff[i - 1];	//差分的前缀和 
	}
	
	int max = -1;
	//记录哪个时间点存在的桶最多 
	for (int i = 1; i <= max_index; i++) {
		if (diff[i] > max) max = diff[i];
	}
	
	cout << max << endl;
	return 0;
}