P4924 [1007] 魔法少女小Scarlet（c,c++）（超详解）

题目描述

Scarlet 最近学会了一个数组魔法，她会在 n×n 二维数组上将一个奇数阶方阵按照顺时针或者逆时针旋转 90∘。

首先，Scarlet 会把 1 到 n2 的正整数按照从左往右，从上至下的顺序填入初始的二维数组中，然后她会施放一些简易的魔法。

Scarlet 既不会什么分块特技，也不会什么 Splay 套 Splay，她现在提供给你她的魔法执行顺序，想让你来告诉她魔法按次执行完毕后的二维数组。

输入格式

第一行两个整数 n,m，表示方阵大小和魔法施放次数。

接下来 m 行，每行 4 个整数 x,y,r,z，表示在这次魔法中，Scarlet 会把以第 x 行第 y 列为中心的 2r+1 阶矩阵按照某种时针方向旋转，其中 z=0 表示顺时针，z=1 表示逆时针。

输出格式

输出 n 行，每行 n 个用空格隔开的数，表示最终所得的矩阵

输入输出样例

输入 #1复制

5 4
2 2 1 0
3 3 1 1
4 4 1 0
3 3 2 1

输出 #1复制

5 10 3 18 15
4 19 8 17 20
1 14 23 24 25
6 9 2 7 22
11 12 13 16 21 

说明/提示

对于50%的数据，满足 r=1

对于100%的数据 1≤n,m≤500，满足 1≤x−r≤x+r≤n,1≤y−r≤y+r≤n。

讲在前排：

        本题的题解用c++写的，但只有头文件和输入输出不同，学c的小伙伴理解起来没有什么问题，头文件替换为自己需要的就行，cin等价于scanf，cout等价于printf，endl就是换行

前排讲的废话比较多，主要是还原自己的思考过程，讲的会比较细，注重一步步的推导，想看代码分析的直接跳到正文就行了

初见这道题时发觉是很明显的模拟题，题意是模拟一个矩阵在某个部分区域进行倒置，最后得到这个矩阵

但见到这个题时还是让我犯了难，主要是两个方面：

1.我不太能理解 Scarlet 会把以第 x 行第 y 列为中心的 2r+1 阶矩阵按照某种时针方向旋转是什么意思

2.矩阵的旋转也是个问题。

没办法了，理解不好，只能自己上手看一看了。

1.首先按样例一写出了一个5*5的矩阵（这些都以给出的第一个样例操作）

2.找出第x行第y列的中心点

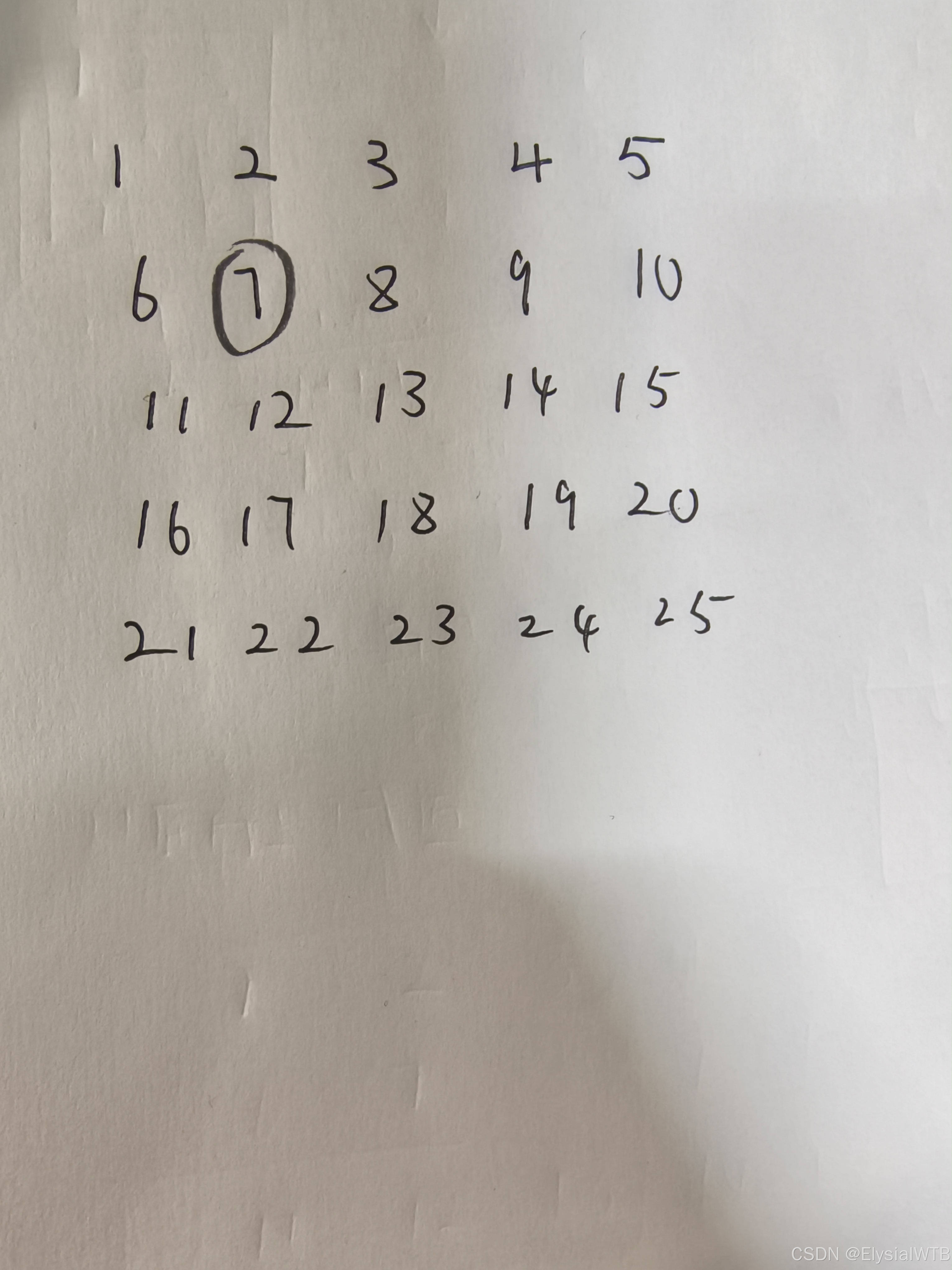
3.嗯......以第2行第2列为中心的2r+1矩阵？那就长这样？

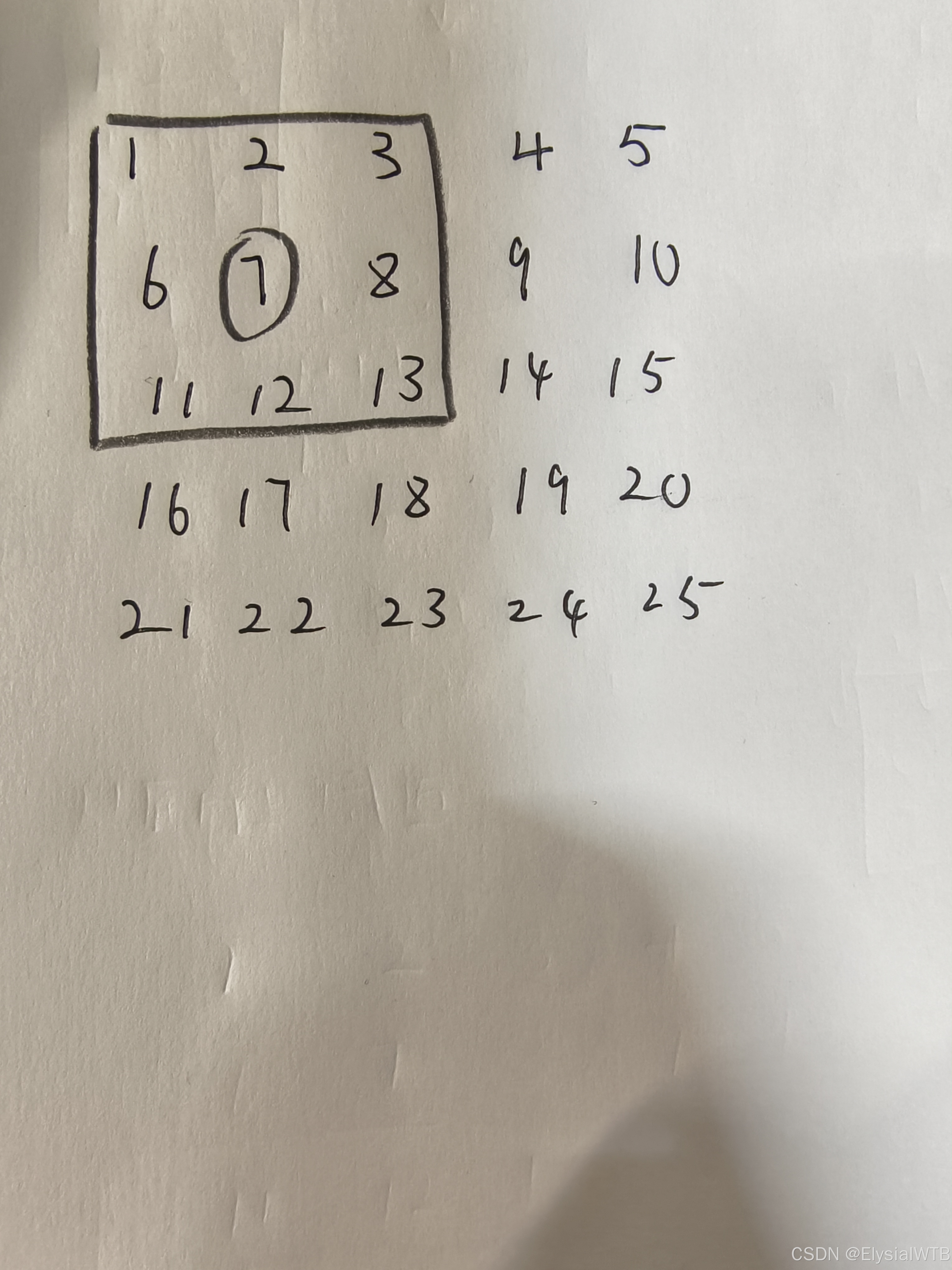
好吧，我悟了，那意思就是在这个框里进行旋转操作呗。

那现在我得明白怎么顺时针和怎么逆时针旋转了，还是自己画图找找规律，我画出了这个小区域顺时针和逆时针旋转后的图片。

以下以顺时针为例，讲讲我的规律是怎么找的，我们知道要想遍历一个二维数组，常用的就是写两个for循环，遍历的顺序从左上角开始，一直往右走，到底后从第二行开始，再一直往右走，以此到最后一行

那么想实现矩阵的旋转，我首先想到拷贝这一小块区域的矩阵起来，希望找到数组下标的规律，让拷贝的小矩阵从上面讲到的遍历顺序能够赋值到我想要的值

思来想去，我想到了这样的规律，看上面的图片，以顺时针旋转为例，我们第一次遍历应该是赋值11，6，1，那这三个数在原数组中哪里呢？哎，这不就在我们的第一列吗。那12，7，2在哪里呢？哎，这不就在我们的第二列吗，那......（想必大家都知道了吗，嘿嘿）

那我们只需要从11开始往上走赋值，走到底后就是完成了第一次循环，再让列往右边移动重复上面的操作开始赋值就行了。

找到这里我们只需要找到它们的下标关系就可以了，题目给出了2r+1的矩阵是有深意的，这意味着以x，y为中心的位置从左边开始和从右边开始长度是一样的，从上边开始和从下边开始的长度也是一样的，那你猜猜，以7为中心（看下边的图），它的左边数字6是在哪一行哪一列呢？答案是第x行，第y-r列。讲到这里差不多也就明朗了，我们的双重for循环不就写出来了吗，第一重是x-r到x+r（第一重是控制行的），第二重是y-r到y+r。

逆时针的我也放在下图：

以上就是我的分析过程了，剩下的也就是代码实现，至少思路方面已经没有问题了，接下来进入正文

正文

写出头文件，这里写成全局变量，因为我会用函数来进行旋转操作，全局变量的话就不用传参进去了，方便很多。

按题意正常赋值，这里有一种思想，那就是题目给出m行，做了m次旋转，我们的解决方法就是写一个m次的循环，在这个循环里面我们进行每一次的操作，这种思想以后我们在很多地方可以用到，大家仔细体会一下。

接下来我们看顺时针旋转的函数

第一个双重for循环我们将a要旋转的区域存放在临时变量中，i和j的起始和终止值我们在前文已经分析过了。第二个双重for循环中，a就是以正常的顺序走下去，而我们的temp将会以我们规定的路线走下去赋值的a。我还是在这里再仔细分析一下temp走路的代码吧：

1.将temp的起始坐标定在了圈起来的小区域的左下角，也就是我们的x+r和y-r

2.然后temp在y1这列一直往上走，也就是x1--

3.内层循环结束后我们将temp的x坐标回归原位，也就是x1 = x+r，同时让temp的列往右边走，也就是y1++。

逆时针的函数如下：

我们来看temp的逆时针路线（大家可以自己分析一下，学会了顺时针，逆时针也不难）：

1.先让temp的坐标的右上角，也就是x-r，y+r的位置

2.temp一直往下走，也就是x1++

3.完成内层循环后我们让temp的x坐标回归原位，也就是x1 = x-r，同时让temp的列往左边走，也就是y1--。

完整代码如下：

#include <bits/stdc++.h>
using namespace std;

int a[505][505];  // 全都作为全局变量，这样就不用函数传参进来了 
int temp[505][505];
int n,m;
int x,y,r,z;

void clockwise(void) //顺时针旋转 
{
	for (int i = x-r; i <= x+r; i++)
	{
		for (int j = y-r; j <= y+r; j++) {
			temp[i][j] = a[i][j];    //将a要逆转的区域存放在temp中 
		}
	} 
	
	int x1 = x+r; // 这是temp的坐标 
	int y1 = y-r;  
	
	//  开始我们的替换吧！！！！
	for (int i = x-r; i <= x+r; i++)
	{
		for (int j = y-r; j <= y+r; j++) {
			a[i][j] = temp[x1][y1];
			x1--; 
		}
		x1 = x+r;
		y1++;
	} 
}





void anticlockwise(void)   //逆时针旋转 
{
	for (int i = x-r; i <= x+r; i++)
	{
		for (int j = y-r; j <= y+r; j++) {
			temp[i][j] = a[i][j];    //将a要逆转的区域存放在temp中 
		}
	} 
	
	int x1 = x-r; // 这是temp的坐标 
	int y1 = y+r;  
	
	//  开始我们的替换吧！！！！
	for (int i = x-r; i <= x+r; i++)
	{
		for (int j = y-r; j <= y+r; j++) {
			a[i][j] = temp[x1][y1];
			x1++; 
		}
		x1 = x-r;
		y1--;
	} 
}


int main()
{
	cin >> n >> m;

	// 按题意给a赋值 
	int k = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			a[i][j] = k++;
		}
	} 
	
	
	//m次旋转，写个m次的循环，在里面进行每一次的操作 
	for (int i = 1; i <= m; i++)
	{
		cin >> x >> y >> r >> z;
		if (z == 1) anticlockwise(); //z==1我们进行逆时针旋转 
		else clockwise();    //顺时针 
	}
	
	
	//输出
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << a[i][j] << " "; 
		}
		cout << endl;
	}  
	
	
	return 0;
}

 

AC如下：

 

最后，本次题解制作不易，为了完整的还原思考的每一步，我写的比较长，花的时间也有点多，大家如果觉得有帮助的话，请帮我点个赞，收藏一下。如果有错误的地方还望海涵