8.13 最小生成树

有向图没有最小生成树。

Prim

Prim算法是针对无向图的求最小生成树的算法。它适用于稠密图。

算法思想：

初始集合设置为空，每次找到距离起点最近的点，将点收入点集，再继续查找距离这个边集最近的点。

初始时，边集为空。

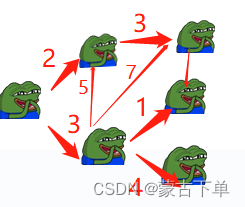
将起点能到达的两个点，设置为待查找。

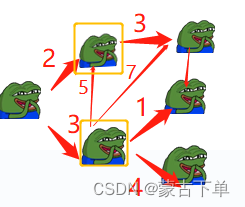
比较发现：2 < 3
将距离最短的结点的边权加入边集。
再将距离最短的结点的后继结点，设置为待查找。

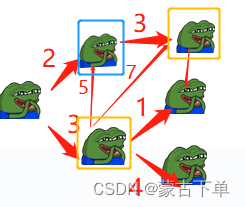
比较发现：3 < INF
将结点加入边集。

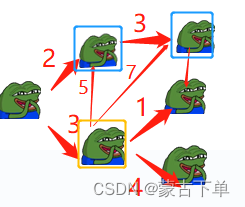
重复上述步骤，直到所有节点都被加入，找到最小生成树：

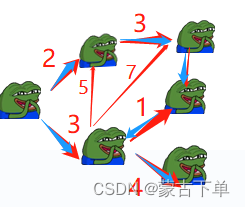
有一条边忘记赋值了但是不想再画图了……就认为它的边权<1吧！

核心代码：

int prim()
{
	memset(dis,0x3f,sizeof dis); 
	int res = 0;//最小生成树的所有边权之和 
	for(int i=0;i<n;i++)
	{
		int t = -1;
		for(int j=1;j<=n;j++)//找到当前在边集s外 距离s最小的点 
		{
			if(!st[j] && t==-1 || dis[t]>dis[j])
			{
				t = j;
			}
		}
		if(i > 0 && dis[t] == INF) return INF;//图不连通，不存在最小生成树 
		if(i > 0) res += dis[t];//将这个点 与边集s中的 某相连点的权值 加入答案 
		
		for(int j=1;j<=n;j++) dis[j] = min(dis[j],g[t][j]);
		//无向图反向建边，权值只取最小 
		st[t] = true;
	}
	return res;
} 

---

Kruskal

Kruskal算法也是求最小生成树的一种算法。它适用于稀疏图。

并查集

在Kruskal算法开始之前，先要引入并查集的概念。

简单来说，并查集，就是询问 合并集合与集合之间的一些操作。

图例详解：

最开始时，列表中的每个点都在不同的集合，指针都指向自己。

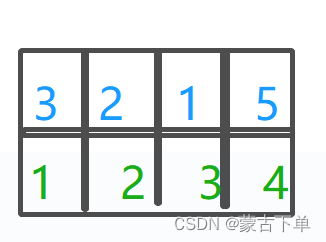
如果要将2 5放入一个集合，即将指针为2 4的集合合并，只需要让2的指针指向5的指针就行了吗？
答案是不。每个指针指向的点都不一样，所以指向的，是要合并的点的父节点。

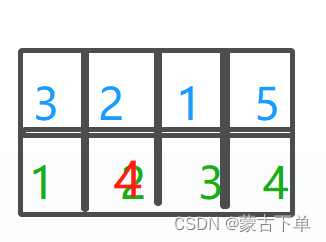
这个就是并查集的基本思想。
下面是并查集经典的find函数，在下面的kruskal代码我们也要用到。

int find(int x)//并查集函数 
{
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
} 

Kruskal代码实现

算法思想：

先将边权升序排序，再判断边权是否已存在于边集。 不存在，就加入集合 。

那么，如何判断它是否已经存在于集合？
这时，我们刚刚所学的并查集就可以用上。

核心代码：

#include<cstring>
#include<iostream>
#include<algorithm> 

const int N = 100010,M = 200010, INF = 0x3f3f3f3f;
int n,m;
int p[N]; //并查集
 
struct Edge{
	int a,b,w;
	
	bool operator<(Edge &w) 
	{
		return w < x.w;
	}
}edges[M];

int cmp(Edge a,Edge b)
{
	return a.w < b.w; 
}
int find(int x)//并查集函数 
{
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
} 

int Kruskal()
{
	sort(edges,edges+m,cmp);//排序 
	
	for(int i=1;i<=n;i++) p[i] = i;//初始化并查集 
	
	int res = 0,cnt = 0;
	for(int i=0;i<m;i++)
	{
		int a = edges[i].a, b= edges[i].b, w = edges[i].w;
		
		a = find(a), b = find(b);
		if(a!=b)//如果a,b不在同一个并查集 
		{
			p[a] = b;//将ab合并 
			res += w;//边权累加 
			cnt++;
		}
	}
	if(cnt < n-1) return INF;//边数小于n-1，不是连通图 
	return res;
} 

---

拓扑排序

由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。
拓扑排序只在有向无环图中存在。

还是这张图，我们给每个小青蛙都标号。

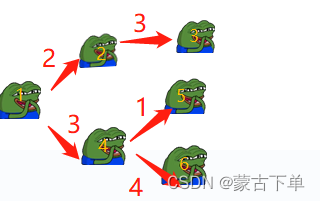
因为拓扑排序要严格按照结点入度的顺序，所以开头一定是1。
2 4号青蛙都是1的后继结点，因此顺序可以调换。
3 5 6也是同理。

代码实现：

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue> 

using namespace std;
const int N=105;

vector<int> g[N];

int din[N];

int n;

void add(int a,int b)
{
	g[a].push_back(b);
}

void topsort()
{
	queue<int> q;
	for(int i=1;i<=n;i++)
	{
		if(din[i]==0) q.push(i);
	}
	while(q.size())
	{
		int t = q.front();
		q.pop();
		
		cout<<t<<" ";
		
		for(int i = 0;i<g[t].size();i++)//遍历点t所有出边并删除 
		{
			int j = g[t][i];
			din[j]--;
			if(din[j]==0) q.push(j);//入度为0 才入队 
		}
	}
}


int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x;
		while(cin>>x,x!=0)
		{
			add(i,x);
			din[x]++;
		}
	}
	topsort();
}