LK（Lucas-Kanade）稀疏光流法

此代码来自《学习OpenCV3中文版》第16章

源代码有点小错误，已修改

LK光流法的基本思想基于以下三个假设。

1.亮度恒定;

2.时间持续性或“微小移动”;

3.空间一致性。

灰度不变假设：同一个空间点的像素灰度值，在各个图像中是固定不变的。

对于t时刻在（x，y）处得像素，在t+dt时刻它运动到（x+dx，y+dy）处。有下式：

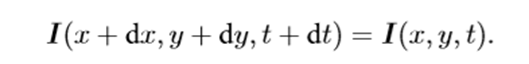
对左边进行泰勒一阶展开，保留一阶项，得： 

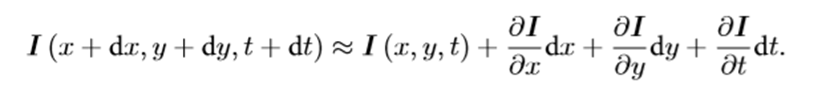
因为下一时刻的灰度等于之前的灰度，有：

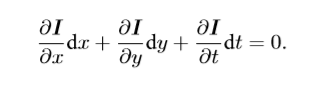
同时除以dt，移项得：

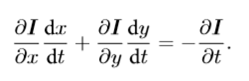
令

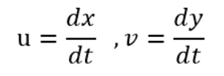
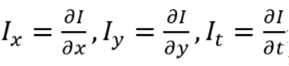
u和v分别表示像素在x轴和y轴上得运动速度；Ix，Iy为图像在x方向和y方向的梯度。It为图像灰度对时间的变化量。

写成矩阵形式

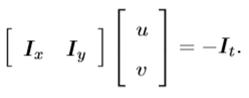
这里只有一个约束方程中，却有两个未知数。这种不确定性称为“孔径问题”。

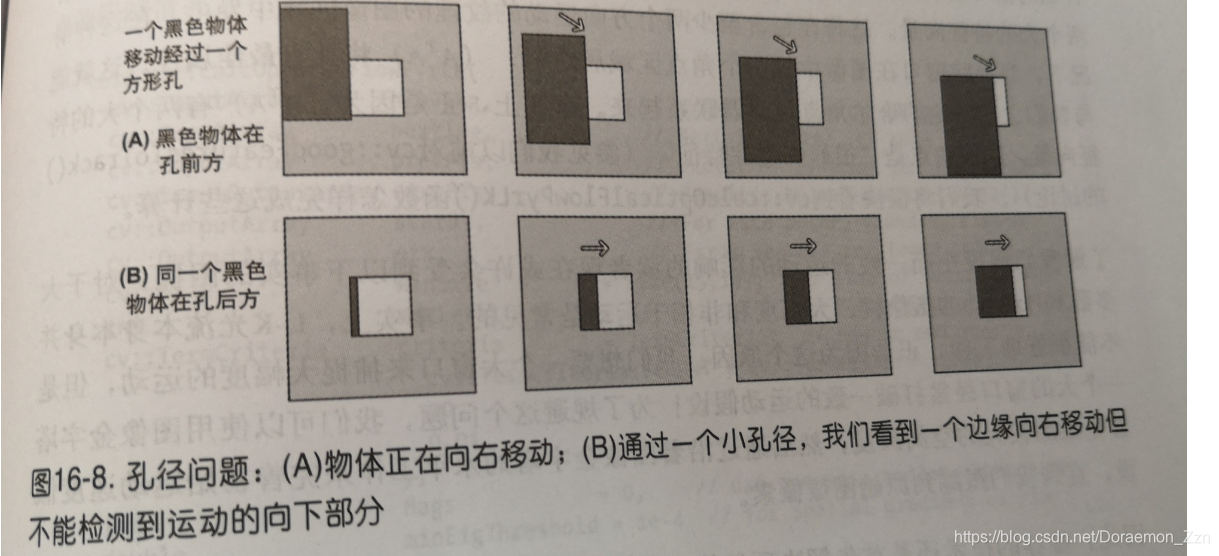
为了解决这个问题，这里就要考虑到三个假设中最后一个假设。如果局部像素斑点相干移动，那么我们可以通过使用周围像素来轻松地求解中心像素的运动来建立方程组。

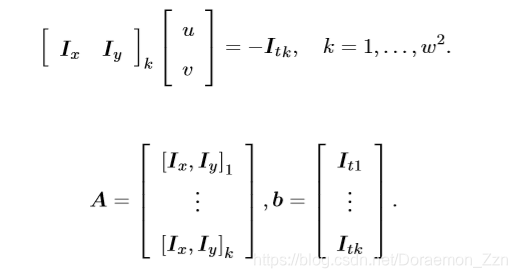
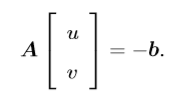
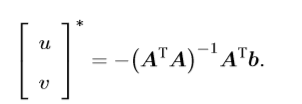
这样就可以求出运动速度u和v。什么时候是可解的呢？当可逆的时候。满秩（rank=2）时是可逆的，此时它有两个较大的特征向量，这就解释了为什么可以和角点检测器连接起来。具体可去看Harris角点的原理。

但是稍微大点的窗口来捕捉大幅度的运动时经常会打破一致的运动假设。为了规避这个问题，可以使用图像金字塔。

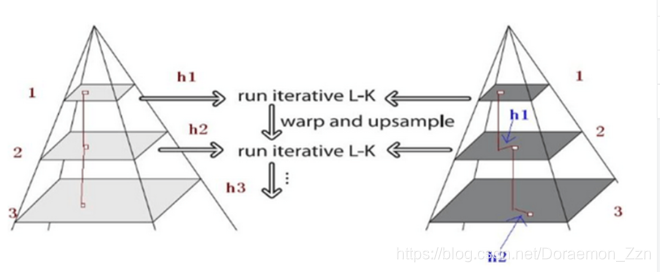
用前一层的运动估计值作为下一层估计运动的起始点。

从顶层开始计算，直到算到底层（原图）。

 

下面是实现的代码

#include <opencv2/opencv.hpp>
#include <chrono>
#include <iostream>

static const int MAX_CORNERS=1000;

void help(char** argv)
{
    std::cout<<"Call:"<<argv[0]<<"[image1][image2]"<<std::endl;
    std::cout<<"Demonstrates Pyramid Lucas-Kanade optical flow."<<std::endl;
}
int main(int argc,char** argv)
{
    std::chrono::steady_clock::time_point t1=std::chrono::steady_clock::now();

    if(argc!=3)
    {help(argv);exit(-1);}


    cv::Mat imgA=cv::imread(argv[1],CV_LOAD_IMAGE_GRAYSCALE);
    cv::Mat imgB=cv::imread(argv[2],CV_LOAD_IMAGE_GRAYSCALE);
    //cv::Size img_sz=imgA.size;
    int win_size=10;
    cv::Mat imgC=cv::imread(argv[2],CV_LOAD_IMAGE_UNCHANGED);

    std::vector<cv::Point2f> cornersA,cornersB;
    const int MAX_CORNERS=500;
    //支持Harris角点检测，也支持Shi Tomasi算法角点检测
    cv::goodFeaturesToTrack(
                imgA,//输入图像
                cornersA,//输出角点vector
                MAX_CORNERS,//最大焦点数目
                0.01,//点的返回质量水平，一般在0.01-0.1之间
                5,//最小距离
                cv::noArray(),//mask=0的点忽略
                3,//使用的领域数
                false,//false="Shi Tomasi"
                0.04//Harris角点检测时使用
                );
    //寻找亚像素角点
    //获得更加精细的角点坐标
    cv::cornerSubPix(
                imgA,
                cornersA,
                cv::Size(win_size,win_size),
                cv::Size(-1,-1),//类似于winsize，Size（-1,-1）表示忽略
                cv::TermCriteria(
                    cv::TermCriteria::MAX_ITER|cv::TermCriteria::EPS,
                    20,
                    0.03
                    )
                );

    std::vector<uchar> features_found;
    cv::calcOpticalFlowPyrLK(          
                imgA,   //初始图像
                imgB,   //最终图像(两者应该具有相同的大小并且具有相同的像素通道)
                cornersA,//第一幅图像的特征输入列表
                cornersB,//第二幅图像中匹配点将被写入的输出列表
                features_found,//输出状态矢量
                cv::noArray(),//输出误差矢量
                cv::Size(win_size*2+1,win_size*2+1),//每个金字塔搜索窗大小
                5,//金字塔层的最大数目
                cv::TermCriteria(
                    cv::TermCriteria::MAX_ITER|cv::TermCriteria::EPS,
                    20,//最大迭代次数
                    0.3//每次迭代最小变化
                    )//告诉算法何时推出搜索匹配
                );

    for(int i=0;i<(int)cornersA.size();i++)
    {
        if(!features_found[i])
            continue;
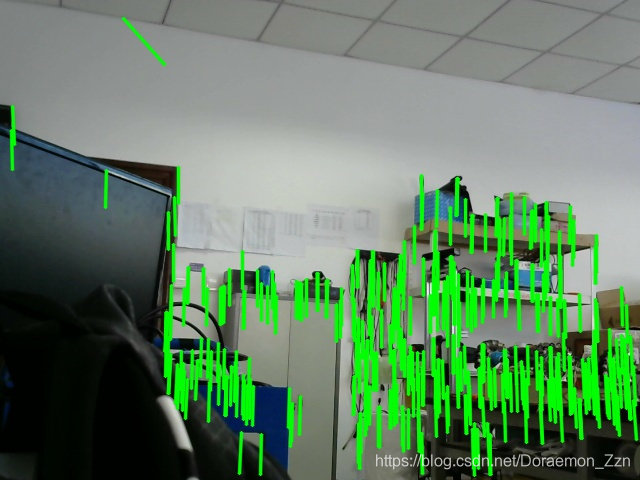
        line(imgC,cornersA[i],cornersB[i],cv::Scalar(0,255,0),2,CV_AA);
    }

    std::chrono::steady_clock::time_point t2=std::chrono::steady_clock::now();
    std::chrono::duration<double> time_used=std::chrono::duration_cast<std::chrono::duration<double>>(t2-t1);
    std::cout<<"LK Flow use time : "<<time_used.count()<<" seconds."<<std::endl;

    cv::imshow("ImageA",imgA);
    cv::imshow("ImageB",imgB);
    cv::imshow("LK Optical Flow Example",imgC);
    cv::imwrite("ImageA.jpg",imgA);
    cv::imwrite("ImageB.jpg",imgB);
    cv::imwrite("LK Optical Flow Example.jpg",imgC);
    cv::waitKey(0);
    return 0;
}

CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
project(LKOpticalFlow)

set(CMAKE_BUILD_TYPE Release)
set(CMAKE_CXX_FLAGS "-std=c++11 -O3")

find_package(OpenCV)
include_directories(${OpenCV_INCLUDE_DIRS})

add_executable(${PROJECT_NAME} "main.cpp")
target_link_libraries(LKOpticalFlow ${OpenCV_LIBS})