学习笔记第三十八节：多项式

最新推荐文章于 2023-07-02 20:33:54 发布

原创最新推荐文章于 2023-07-02 20:33:54 发布 · 688 阅读

1 ·

CC 4.0 BY-SA版权

学习笔记同时被 2 个专栏收录

61 篇文章

订阅专栏

数论

49 篇文章

订阅专栏

本文深入探讨了多项式在算法中的应用，包括快速傅里叶变换（FFT）、NTT及其变种，以及多项式的求逆、取模、对数、指数等高级运算。文章还介绍了多项式的多点求值、快速插值、转换技巧和优化方法，如myy优化，为读者提供了丰富的算法实践案例。

正题

下述的所有例题可在洛谷上搜索“多项式”，找到。

Contents:

快速傅里叶变换
NTT
任意模数NTT
多项式求逆
多项式取模
多项式ln
多项式exp
多项式多点求值
多项式快速插值
普通多项式转下降幂多项式
下降幂多项式转普通多项式

快速傅里叶变换

可以到我的blog学习，尽管写得不太好。

NTT

可以发现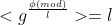 $<g^{\frac{\phi(mod)}{l}}>=l$ ，具体证明可以参考我的blog。所以就可以满足l次单位根的性质。

任意模数NTT

可以发现，如果使用三模数合并或者拆系数NTT只能达到9或7次的DFT。

针对拆系数NTT使用myy优化可以将此升级使得只用4次DFT可以完成。

首先假设现在已经被分成 $A(x),B(x),C(x),D(x)$ 四个多项式。

现在目的是求 $A(x)C(x),A(x)D(x),B(x)C(x),B(x)D(x)$

我们思路清晰，先求出A和B的DFT，再求出 $E(x)=C(x)+iD(x)$ 的DFT。

然后设 $c1(x)=A(x)*E(x),c2(x)=B(x)*E(x)$ ，那么c1(x)的实部就为AC，虚部就为AD，c2同理。

因为A卷E实际上实部虚部可以分开考虑，反正最后对另一部分的影响都是0.

那么我们现在用了5次DFT，其实加上FFT相对于NTT的常数快不了多少。

所以我们还要优化，考虑 $Q(x)=A(x)+B(x)i$ 。

经过一系列推导（大概就是 $Q(\omega_n^j),Q(\omega_n^{-j})$ 关于AB的方程列出来）有：

$\\A(\omega_n^j)=\frac{Q(\omega_n^j).a+Q(\omega_n^{-j}).a}{2}+i\frac{Q(\omega_n^j).b-Q(\omega_n^{-j}).b}{2} \\B(\omega_n^j)=\frac{Q(\omega_n^j).b+Q(\omega_n^{-j}).b}{2}+i\frac{-Q(\omega_n^j).a+Q(\omega_n^{-j}).a}{2}$

这样写只是好看，如果想记得方便可以试试将同一个复数得实部虚部放到一起。

那么我们只需要对Q做一次DFT就可以用O(n)的时间算出A和B的DFT了。

就变成4次DFT了，时间大概是三模数NTT的1/7。

多项式求逆

$\\F_0(x)G_0(x)\equiv 1(\mod x^{\left \lceil \frac{n}{2} \right \rceil}) \\(F_0(x)G_0(x)-1)^2\equiv F_0^2(x)G_0^2(x)-2F_0(x)G_0(x)+1\equiv0(\mod x^n) \\G(x)\equiv 2G_0(x)-F(x)G_0(x)^2$

每一步都很显然，可以直接递归。时间复杂度 $T(n)=T(\left \lceil \frac{n}{2} \right \rceil)+O(n \log_2n)=O(n\log_2n)$

多项式取模

多项式取模需要多项式除法，所以咱们一起说。

$H(x)G(x)+R(x)\equiv F(x)$

我们定义一个n次多项式 $F_R(x)=x^nF(\frac{1}{x})$ ，通俗易懂的来说就是把他的每一项系数翻转过来。

那么

$\\ H(x)x^mG(x)x^{n-m}+R(x)x^{m-1}x^{n-m+1}\equiv F(x)x^n \\ H(\frac{1}{x})x^mG(\frac{1}{x})x^{n-m}+R(\frac{1}{x})x^{m-1}x^{n-m+1}\equiv F(\frac{1}{x})x^n \\H_R(x)G_R(x)\equiv F_R(x) (\mod x^{n-m+1}) \\G_R(x)\equiv F_R(x)H_R^{-1}(x)$

就可以推出上面这些东西，直接用多项式求逆求解G。

然后根据定义求出R就可以了。

在讲多项式ln和多项式exp之前，我们先来说一说泰勒展开这个东西。

泰勒有一天想，对于这些ln和exp这些函数无限项的函数，求出一某个点的值显得很困难。

比如说 $\ln 2,e^2$ ......

那么泰勒这样想：我们可以用一条有限项的函数来贴近这条函数。

假设这个函数是 $G(x)=g_0+g_1x^1+g_2x^2+...+g_nx^n$

那么这个函数需要满足什么样的性质呢？

首先：常数项相等，也就是 $g_0=f_0$ ，其次，他们在 $x=0$ 时的导数相等，那么就是 $g_1*1=f'(0)$ 。

他们的二阶导应该也相等： $g_2*2*1=f''(0)$ ......

那么就有 $G(x)=f(0)+\frac{f'(0)}{1}x+\frac{f''(0)}{2!}x^2+...+\frac{f^{(n)}}{n!}x^n$

把 $x=0\to x=a$ ，就变成了 $G(x)=f(a)+\frac{f'(a)}{1}(x-a)+\frac{f''(a)}{2!}(x-a)^2+...+\frac{f^{(n)}}{n!}(x-a)^n$ 。

可以根据导数运算法则自己推一推。

在我的blog里面有常用的泰勒展开公式。

多项式ln

按照我的理解，将 $\ln(x)$ 在1的位置展开，那么 $\ln(x)=\sum_{i=0}(-1)^{i}\frac{(x-1)^{i+1}}{(i+1)!}$

可以看到，如果第一位为1，那么第n项只会被 $i\in[0,n)$ 影响到，所以就会在某个时刻被确定下来，否则永远不会确定下来。

根据复合函数求导法则，可以看到： $\ln(F(x))=\int \frac{F'(x)}{F(x)}$ 。

这样就做完了。

多项式exp

按照我的理解，将 $e^x$ 在0的位置展开，那么 $e^x=\sum_{i=0}\frac{x^i}{i!}$

如果多项式的第一位为0，那么第n项只会被 $i\in[0,n)$ 影响到，所以就会在某个时刻被确定下来，否则永远不会确定下来。

$\\F(x)=e^{A(x)} \\\ln F(x)=A(x)$

构造多项式函数 $G(F(x))=\ln F(x)-A(x)$

相当于找G的一个零点。

假设前 $\left \lceil \frac{n}{2} \right \rceil$ 项已经做出来了， $G(F_0(x))=\ln F_0(x)-A(x)(\mod x^{\left \lceil \frac{n}{2} \right \rceil})$

喜闻乐见的，我们将G在 $F_0(x)$ 的位置展开，得到： $G(F(x))=G(F_0(x))+G'(F_0(x))(F(x)-F_0(x))(\mod x^n)$

为什么没有后面了？因为平方一定是0.

那么一下解式子可以得到： $F(x)=F_0(x)(1-\ln F_0(x)+A(x)) (\mod x^n)$

做完了，常数极大。

多项式多点求值

可以很容易理解，将a代入一个多项式之后的权值相当于这个多项式对 $(x-a)$ 取模的常数项。

可以考虑一个 $x^n\to ax^{n-1}\to a^2x^{n-2}\to...\to a^n$

那么多点求值，我们处理出来 $\prod_{i=l}^{mid} (x-x_i) ,\prod_{i=mid+1}^r (x-x_i)$ ，然后分治就可以了，常数极大。

多项式快速插值

首先拉格朗日插值法可以得到： $F(x)=\sum_{i=1}^ny_i\prod_{j\not = i}\frac{x-x_j}{x_i-x_j}$

然后先考虑系数： $G(x)=\frac{\prod_{i=1}^n x-x_i}{x-x}$

那么原来的式子就变成了： $F(x)=\sum_{i=1}^nG(x_i)\prod_{j\not=i}(x-x_j)$

但是你会发现这个G没法求。

就要用到洛必达法则： $\frac{\lim_{x\to a}A(x)}{\lim_{x\to a}B(x)}=\frac{\lim_{x\to a}A'(x)}{\lim_{x\to a}B'(x)}$

那么 $G(x)=(\prod_{i=1}^n x-x_i)'$

求出系数后分治就可以了，先预处理出 $\prod_{i=l}^{mid} (x-x_i) ,\prod_{i=mid+1}^r (x-x_i)$ ，常数极大。

普通多项式转下降幂多项式

这个要用到第二类斯特林数。

$x^n=\sum_{i=0}^{n} P_x^iS(n,i)$

然后全部带进去就可以得到：

$F(x) \\=\sum_{i=0}^{n-1}a_ix^i \\=\sum_{i=0}^{n-1}a_i\sum_{j=0}^ix^{\underline j}S(i,j) \\=\sum_{j=0}^{n-1}x^{\underline j}\sum_{i=j}^{n-1}a_iS(i,j)$

所以我们要求的就是后面那个东西，发现 $S(i,j)=0|i<j$ 。所以i可以从0开始枚举：

$\sum_{i=0}^{n-1}a_i\frac{1}{j!}\sum_{k=0}^j(-1)^{j-k}C_j^kk^i \\=\sum_{i=0}^{n-1}a_i\sum_{k=0}^j\frac{(-1)^{j-k}}{(j-k)!}\frac{k^i}{k!} \\=\sum_{k=0}^n\frac{(-1)^{j-k}}{(j-k)!}\sum_{i=0}^n\frac{a_ik^i}{k!}$

前面可以直接预处理，后面这个需要多点求值，最后卷积即可。

下降幂多项式转普通多项式

比上面那个东西简单，发现我们只需要求出来 $x={0,...,n-1}$ 的点值就可以了。

发现，当 $x=i$ 时，对于 $k<=i$ 时， $a_k$ 的贡献是 $\frac{i!}{(i-k)!}$ ，那么我们先不管 $i!$ ，最后乘上就可以了。

所以相当于 $a*e$ 。

后面就是插值的事情了，但是发现慢就慢在求系数的过程。

发现系数也是可以用阶乘预处理出来的，那么系数就很小了。

#include<bits/stdc++.h>
#define vi vector<int>
using namespace std;

const int mod=998244353;
int ksm(int x,int t){
	int tot=1;
	while(t){
		if(t&1) tot=1ll*tot*x%mod;	
		x=1ll*x*x%mod;
		t/=2;
	}
	return tot;
}
const int N=3000010,I=ksm(3,(mod-1)/4),Iinv=ksm(I,mod-2);
int where[N],limit;
int poor[30000010],inv[N];
int*now=poor;
int*w[2][25];
void pre(){
	inv[1]=1;for(int i=2;i<=3000000;i++) inv[i]=1ll*inv[mod%i]*(mod-mod/i)%mod;
	for(int l=2,u=0;u<22;u++,l<<=1){
		w[0][u]=now;now+=l+1;
		w[1][u]=now;now+=l+1;
		w[0][u][0]=1;w[0][u][1]=ksm(3,(mod-1)/l);
		for(int i=2;i<=l;i++) w[0][u][i]=1ll*w[0][u][i-1]*w[0][u][1]%mod;
		for(int i=0;i<=l;i++) w[1][u][i]=w[0][u][l-i];
	}
}

void prepare(int n){
	int l=0;limit=1;
	while(limit<=n) limit<<=1,l++;
	for(int i=0;i<limit;i++) where[i]=((where[i>>1]>>1)|((i&1)<<(l-1)));
}

void DFT(vi&now,int op){
	for(int i=0;i<limit;i++) if(i<where[i]) swap(now[i],now[where[i]]);
	for(int l=1,u=0;l<limit;l<<=1,u++){
		for(int i=0;i<limit;i=i+l+l){
			for(int x=i,y=i+l,v=0;y<i+l+l;x++,y++,v++){
				int a=now[x],b=1ll*now[y]*w[op][u][v]%mod;
				now[x]=a+b;now[x]>=mod?now[x]-=mod:0;
				now[y]=a+mod-b;now[y]>=mod?now[y]-=mod:0;
			}
		}
	}
	if(op){
		int tmp=ksm(limit,mod-2);
		for(int i=0;i<limit;i++) now[i]=1ll*now[i]*tmp%mod;
	}
}

vi operator*(vi f,vi g){
	int tot=f.size()+g.size()-2;
	prepare(tot);
	f.resize(limit);g.resize(limit);
	DFT(f,0),DFT(g,0);
	for(int i=0;i<limit;i++) f[i]=1ll*f[i]*g[i]%mod;
	DFT(f,1);f.resize(tot+1);
	return f;
}

vi operator-(vi f,vi g){
	int n=max(f.size(),g.size());
	if(f.size()==n){
		for(int i=0;i<g.size();i++) f[i]=f[i]+mod-g[i],f[i]>=mod?f[i]-=mod:0;
		return f;
	}
	else {
		for(int i=0;i<f.size();i++) g[i]=f[i]+mod-g[i],g[i]>=mod?g[i]-=mod:0;
		for(int i=f.size();i<n;j++) g[i]=mod-g[i],g[i]>=mod?g[i]-=mod:0;
		return g;
	}
}

vi operator+(vi f,vi g){
	int n=max(f.size(),g.size());
	if(f.size()==n){
		for(int i=0;i<g.size();i++) f[i]=f[i]+g[i],f[i]>=mod?f[i]-=mod:0;
		return f;
	}
	else {
		for(int i=0;i<f.size();i++) g[i]=f[i]+g[i],g[i]>=mod?g[i]-=mod:0;
		return g;
	}
}

void INV(vi&h){
	int n=h.size();
	if(n==1) {h[0]=ksm(h[0],mod-2);return ;}
	vi f0=h;f0.resize((n+1)/2);INV(f0);
	prepare(n+2*(n+1)/2-3);
	h.resize(limit);f0.resize(limit);
	DFT(h,0);DFT(f0,0);
	for(int i=0;i<limit;i++) 
		h[i]=(2ll*f0[i]+mod-1ll*f0[i]*f0[i]%mod*h[i]%mod)%mod;
	DFT(h,1);h.resize(n);
}

vi operator/(vi f,vi g){
	int n=f.size(),m=g.size();
	reverse(f.begin(),f.end());
	reverse(g.begin(),g.end());
	f.reszie(n-m+1);g.resize(n-m+1);INV(g);
	g=f*g;g.resize(n-m+1);reverse(g.begin(),g.end());
	while(g.size() && !g.back()) g.pop_back();
	return g;
}

vi operator%(vi f,vi g){
	vi ans=f-f/g*g;ans.resize(g.size()-1);
	return ans;
}

void LN(vi&h){	
	int n=h.size();
	vi g;g=h;INV(g);
	for(int i=0;i<n-1;i++) h[i]=1ll*h[i+1]*(i+1)%mod;
	h[n-1]=0;h=h*g;
	for(int i=n-1;i>=1;i--) h[i]=1ll*h[i-1]*inv[i]%mod;
	h[0]=0;h.resize(n);
}

void EXP(vi&h){
	int n=h.size();
	if(n==1) {h[0]=1;return ;}
	vi f0=h;f0.resize((n+1)/2);EXP(f0);
	vi g=f0;g.resize(n);LN(g);
	for(int i=0;i<n;i++) h[i]=g[i]+mod-h[i],h[i]>=mod?h[i]-=mod:0;
	prepare(n<<1);h.resize(limit);f0.resize(limit);
	DFT(h,0),DFT(f0,0);
	for(int i=0;i<limit;i++) h[i]=1ll*f0[i]*(mod+1-h[i])%mod;
	DFT(h,1);h.resize(n);
}

void KSM(vi&f,int a,int b,bool full){//k mod , k mod-1 , k >= n
	int n=f.size(),c,d=n;
	for(int i=0;i<n;i++) if(f[i]) {c=f[i],d=i;break;}
	if(d && full || 1ll*d*a>=n){
		for(int i=0;i<n;i++) f[i]=0;
		return ;
	}
	int tmp=ksm(c,mod-2);c=ksm(c,b);
	for(int i=0;i<n-d;i++) f[i]=1ll*f[i+d]*tmp%mod;
	f.resize(n-d);LN(f);
	for(int i=0;i<n-d;i++) f[i]=1ll*f[i]*a%mod;
	EXP(f);f.resize(n);
	for(int i=n-1;i>=d*a;i--) f[i]=1ll*f[i-d*a]*c%mod;
	for(int i=0;i<d*a;i++) f[i]=0;
}

int Cipolla(int x){
	int a=rand()%998244353;
	while(ksm(1ll*a*a%mod+mod-x,(mod-1)/2)==1) a=rand()%998244353;
	int tmp=1ll*a*a%mod+mod-x;tmp>=mod?tmp-=mod:0;
	int x1=1,y1=0,x2=a,y2=1,t=(mod+1)/2;
	while(t){
		if(t&1){
			int tx=x1,ty=y1;
			x1=1ll*tx*x2%mod+1ll*ty*y2%mod*tmp%mod,x1>=mod?x1-=mod:0;
			y1=1ll*tx*y2%mod+1ll*x2*ty%mod,y1>=mod?y1-=mod:0;
		}
		int tx=x2,ty=y2;
		x2=1ll*tx*tx%mod+1ll*ty*ty%mod*tmp%mod,x1>=mod?x1-=mod:0;
		y2=2ll*tx*ty%mod;
		t/=2;
	}
	return min(x1,mod-x1);
}

void KF(vi&f){
	int n=f.size();
	if(n==1) {f[0]=Cipolla(f[0]);return ;}
	vi f0=f;f0.resize((n+1)/2);KF(f0);
	vi g=f0;g.resize(n);INV(g);
	f=f*g+f0;f.resize(n);
	for(int i=0;i<n;i++) f[i]=1ll*f[i]*inv[2]%mod;
}

void SIN(vi&f){
	int n=f.size();
	vi g=f;
	for(int i=0;i<n;i++) f[i]=1ll*f[i]*I%mod,g[i]=1ll*g[i]*(mod-I)%mod;
	EXP(f);EXP(g);
	f=f-g;
	for(int i=0;i<n;i++) f[i]=1ll*f[i]*Iinv%mod*inv[2]%mod;
}

void COS(vi&f){
	int n=f.size();
	vi g=f;
	for(int i=0;i<n;i++) f[i]=1ll*f[i]*I%mod,g[i]=1ll*g[i]*(mod-I)%mod;
	EXP(f);EXP(g);f=f+g;
	for(int i=0;i<n;i++) f[i]=1ll*f[i]*inv[2]%mod;
}

vi p[N];

void MPpre(vi&a,int now,int l,int r){
	if(l==r){
		p[now].resize(2);
		p[now][1]=1;p[now][0]=mod-a[l];
		return ;
	}
	int mid=(l+r)/2;
	MPpre(a,now<<1,l,mid);MPpre(a,now<<1|1,mid+1,r);
	p[now]=p[now<<1]*p[now<<1|1];
}

void MPgas(vi f,vi&g,int now,int l,int r){
	if(f.size()>=p[now].size()) f=f%p[now];
	if(l==r){g[l]=f[0];return ;}
	int mid=(l+r)/2;
	MPgas(f,g,now<<1,l,mid);MPgas(f,g,now<<1|1,mid+1,r);
}

void MP(vi&f,vi&a,vi&g){
	MPpre(a,1,0,a.size()-1);
	MPgas(f,g,1,0,a.size()-1);
}

vi FITgas(vi&g,int now,int l,int r){
	if(l==r){
		vi f;f.resize(1);f[0]=g[l];
		return f;
	}
	int mid=(l+r)/2;
	return FITgas(g,now<<1,l,mid)*p[now<<1|1]+FITgas(g,now<<1|1,mid+1,r)*p[now<<1];
}

vi FIT(vector<pair<int,int> >&V){
	int n=V.size();
	vi a;a.resize(n);
	for(int i=0;i<n;i++) a[i]=V[i].first;
	MPpre(a,1,0,n-1);
	vi g=p[1];
	for(int i=0;i<g.size()-1;i++) g[i]=1ll*g[i+1]*(i+1)%mod;
	g.resize(g.size()-1);
	vi b;b.resize(n);MPgas(g,b,1,0,n-1);
	for(int i=0;i<n;i++) b[i]=1ll*V[i].second*ksm(b[i],mod-2)%mod;
	return FITgas(b,1,0,n-1);
}