学习笔记第八节：树链剖分

最新推荐文章于 2022-03-16 09:22:12 发布

原创最新推荐文章于 2022-03-16 09:22:12 发布 · 457 阅读

0 ·

CC 4.0 BY-SA版权

学习笔记专栏收录该内容

61 篇文章

订阅专栏

正题

~~树链剖分+树状数组套主席树似乎可以解决大多数树上求状态的问题哦~~

我们一起来学树链剖分吧！

树链剖分的宗旨是：让一条链上的编号连续，使得路径分割成多个部分。

如下图：

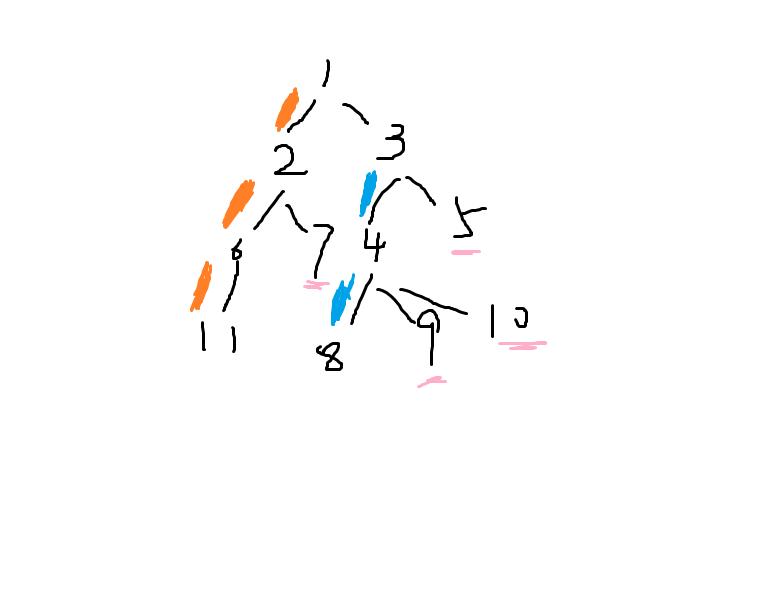
求求你看看我的图。。

橙色表示的是一条链，蓝色表示的是另外一条链，而粉色的点不在任何一条链上，怎么办，把它自己看成一条链。

因为我们要让一条链上的编号连续，所以，接下来我们来对它重新编号。

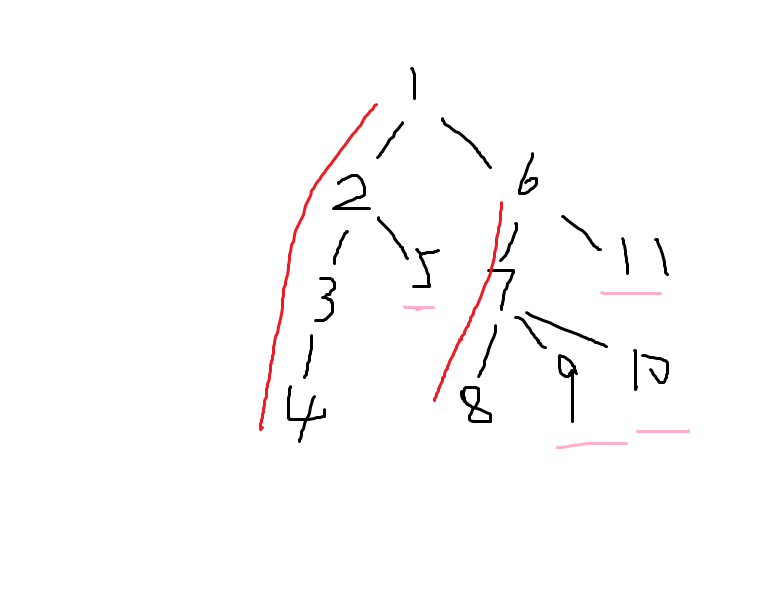
所以我们让一条链上的编号连续有什么用呢？

这可以使得我们用树状数组或线段树来维护。

因为它编号连续，所以它在线段树中的编号就连续。

那么假如我们要求x到y的的和（带修），就一定可以拆成很多条子链（emm）。比如上图，我们要求4到9（新编号）的和，就可以拆成（1，4），（6，7），（9，9），三个区间，我们去线段树或树状数组中求一下和即可。

那么找链的依据又是什么呢？怎样找链可以使得时间大大提高呢？

重链

我们可以这样想，链是有一堆连续的点组成的，而且除了第一个点之外，其他点都有父亲。

所以我们提出一个概念：重儿子。

重儿子指的是儿子为根子树最大（节点最多）的儿子。

重儿子的衔接形成重链

接着，我们很容易就可以通过不断的跳到当前链顶端来实现区间的变化。

代码详解

我们先进行第一次的dfs来找出重儿子。

void dfs_1(int x){
	tot[x]=1;//tot为x为x所在子树的大小
	for(int i=first[x];i!=0;i=s[i].next){//找出相邻的点
		int y=s[i].y;
		if(y!=fa[x]){//相邻且不为父亲
			dep[y]=dep[x]+1;//更新深度
			fa[y]=x;//更新y的父亲
			dfs_1(y);//更新y子树
			if(tot[y]>tot[son[x]]) son[x]=y;//如果y所在子树比原先的重儿子还要大，那么就让y当我的重儿子
			tot[x]+=tot[y];//累加tot
		}
	}
}

很明显我们知道，tot和son的继承是要处理完子树节点才能知道的，所以要搞清楚。

第二次dfs来找出重链并对其上面的节点进行编号，同时要处理出一个top，表示x所在重链的顶端。

void dfs_2(int x,int tp){//tp为将要赋值的顶端
	len++;
	top[x]=tp;image[x]=len;fact[len]=x;//更新image（新编号），fact（旧编号）
	if(son[x]!=0) dfs_2(son[x],tp);//有重儿子继续往重儿子跑
	for(int i=first[x];i!=0;i=s[i].next){//更新其他不为重儿子的儿子
		int y=s[i].y;
		if(y!=fa[x] && y!=son[x]) dfs_2(y,y);//自己必定为新重链的顶端
	}
}

如果你听到这里，那么你很强大；如果你还可以继续停下来，那你就是最棒的！！

接着我们用线段树来处理区间和（新编号），这个没必要解释，虽然我写的是函数式线段树。

关键是怎么用树剖来往上跳。

int get_sum(){
	int x,y;
	scanf("%d %d",&x,&y);
	int tx=top[x],ty=top[y];//tx为x所在重链所在的顶端，ty为y所在重链的顶端
	int ans=0;
	while(tx!=ty){//不在一条重链上，说明还没有到lca
		if(dep[ty]<dep[tx]){//优先top在下面的翻上来，在这里统一改成y
			swap(tx,ty);
			swap(x,y);
		}
		ans+=query_sum(root,image[ty],image[y],1,n);//top到当前点的编号肯定连续，丢进线段树求和
		y=fa[ty];ty=top[y];
	}
	if(dep[x]>dep[y]) swap(x,y);//在让深度小的在上面
	ans+=query_sum(root,image[x],image[y],1,n);//统计答案
	return ans;返回
}

大家可以用[ZJOI2008]树的统计来作为例题。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int ls[100010],rs[1000010];
int sum[100010],mmax[100010];
int n,m;
struct edge{
	int y,next;
}s[100010];
int first[30010];
int len=0;
int dep[30010],tot[30010],fa[30010],son[30010],top[30010];
int image[30010],fact[30010];
int num[30010];
int root;
int d,v;
bool tf=false;

void ins(int x,int y){
	len++;
	s[len].y=y;s[len].next=first[x];first[x]=len;
}

void dfs_1(int x){
	tot[x]=1;
	for(int i=first[x];i!=0;i=s[i].next){
		int y=s[i].y;
		if(y!=fa[x]){
			dep[y]=dep[x]+1;
			fa[y]=x;
			dfs_1(y);
			if(tot[y]>tot[son[x]]) son[x]=y;
			tot[x]+=tot[y];
		}
	}
}

void dfs_2(int x,int tp){
	len++;
	top[x]=tp;image[x]=len;fact[len]=x;
	if(son[x]!=0) dfs_2(son[x],tp);
	for(int i=first[x];i!=0;i=s[i].next){
		int y=s[i].y;
		if(y!=fa[x] && y!=son[x])
			dfs_2(y,y);
	}
}

void update(int &now,int l,int r){
	if(now==0) now=++len;
	sum[now]+=d;
	mmax[now]=-1e9;
	if(l==r){
		if(tf) mmax[now]=d;
		return ;
	}
	if(v<=(l+r)/2) update(ls[now],l,(l+r)/2);
	else update(rs[now],(l+r)/2+1,r);
	mmax[now]=max(mmax[ls[now]],mmax[rs[now]]);
}

void change(){
	int x,y;
	scanf("%d %d",&x,&y);
	d=-num[x];v=image[x];tf=false;
	update(root,1,n);
	d=num[x]=y;tf=true;
	update(root,1,n);
}

int query_max(int now,int l,int r,int x,int y){
	if(x==l && r==y) return mmax[now];
	int mid=(x+y)/2;
	if(r<=mid) return query_max(ls[now],l,r,x,mid);
	else if(mid<l) return query_max(rs[now],l,r,mid+1,y);
	else return max(query_max(ls[now],l,mid,x,mid),query_max(rs[now],mid+1,r,mid+1,y));
}

int get_max(){
	int x,y;
	scanf("%d %d",&x,&y);
	int tx=top[x],ty=top[y];
	int	ans=-1e9;
	while(tx!=ty){
		if(dep[ty]<dep[tx]){
			swap(tx,ty);
			swap(x,y);
		}
		ans=max(ans,query_max(root,image[ty],image[y],1,n));
		y=fa[ty];ty=top[y];
	}
	if(dep[x]>dep[y]) swap(x,y);
	ans=max(ans,query_max(root,image[x],image[y],1,n));
	return ans;
}

int query_sum(int now,int l,int r,int x,int y){
	if(x==l && r==y) return sum[now];
	int mid=(x+y)/2;
	if(r<=mid) return query_sum(ls[now],l,r,x,mid);
	else if(mid<l) return query_sum(rs[now],l,r,mid+1,y);
	else return query_sum(ls[now],l,mid,x,mid)+query_sum(rs[now],mid+1,r,mid+1,y);
}

int get_sum(){
	int x,y;
	scanf("%d %d",&x,&y);
	int tx=top[x],ty=top[y];
	int	ans=0;
	while(tx!=ty){
		if(dep[ty]<dep[tx]){
			swap(tx,ty);
			swap(x,y);
		}
		ans+=query_sum(root,image[ty],image[y],1,n);
		y=fa[ty];ty=top[y];
	}
	if(dep[x]>dep[y]) swap(x,y);
	ans+=query_sum(root,image[x],image[y],1,n);
	return ans;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n*2;i++) mmax[i]=-1e9;
	for(int i=1;i<=n-1;i++){
		int x,y;
		scanf("%d %d",&x,&y);
		ins(x,y);ins(y,x);
	}
	dep[1]=1;fa[1]=0;dfs_1(1);
	len=0;dfs_2(1,1);
	len=0;
	for(int i=1;i<=n;i++){
		int x;
		scanf("%d",&x);
		num[i]=x;
		v=image[i];d=x;
		tf=true;
		update(root,1,n);
	}
	scanf("%d",&m);
	char ch[10];
	while(m--){
		scanf("%s",ch);
		if(ch[1]=='H') change();
		else if(ch[1]=='M') printf("%d\n",get_max());
		else if(ch[1]=='S') printf("%d\n",get_sum());
	}
}

谢谢