K值近邻法的简单运用

K值近邻法的介绍

K值近邻法是聚类的一种方法，它由近邻法改进而得，从而减少一定的失误。原理：在目标点附近找到与其距离最短的K个点，然后判断这K个点分别在哪一类，最后看哪一类中点的数目更多。因此我们常取K为奇数，这个原理有点类似于投票机制。

K值近邻法的运用

这里我用的R语言来分析：

简单应用

• 第一步：先准备数据，这里我用一张图来看看我的数据；

• 第二步：利用R语言来处理

  • 首先对数据进行标准化，消除量纲影响

autonorm <-function(data){
  min <- min(data)
  max <- max(data)
  for(i in 1:length(data))
    data[i]<-(data[i]-min)/(max-min)
  return(data)
}

• 然后用两个数据试一下

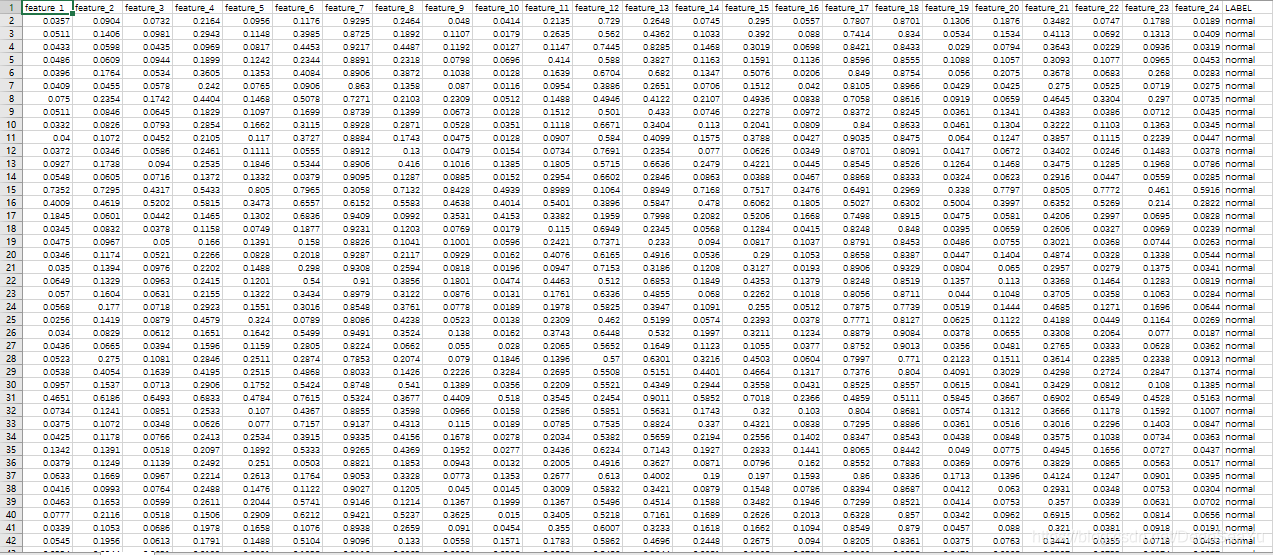
da <- read.csv("E:/test/shiyan.csv",header = T,sep = ',')
de <- apply(as.matrix(da[,1:24]),2,autonorm)
x <- da[13,1:24]
y <- da[79,1:24]
x <- (x-apply(da[c(-13,-79),1:24],2,min))/(apply(da[c(-13,-79),1:24],2,max)-apply(da[c(-13,-79),1:24],2,min))
y <- (y-apply(da[c(-13,-79),1:24],2,min))/(apply(da[c(-13,-79),1:24],2,max)-apply(da[c(-13,-79),1:24],2,min))
dis<-rep(0,length(de[,1]))
for(i in 1:length(de[,1])){
  dis[i]<-sqrt(sum((x-de[i,1:24])^2))
}
table(de[order(dis)[1:5],5])
for(i in 1:length(de[,1])){
  dis[i]<-sqrt(sum((y-de[i,1:24])^2))
}
table(de[order(dis)[1:5],5])

R包的使用

• class 包（自带）

library(class)
da <- read.csv("E:/test/shiyan.csv",header = T,sep = ',')
de <- sample(1:nrow(da),191)
da.train <- da[de,]
da.test <- da[-de,]
train <- da.train[,-25]
test <- da.test[,-25]
result.KNN <- knn(train,test,cl=da.train$LABEL)
table(result.KNN,da.test$LABEL)

• kknn 包

library(kknn)
da <- read.csv("E:/test/shiyan.csv",header = T,sep = ',')
m <- dim(da)[1]
val <- sample(1:m,size = 40,replace = FALSE,prob= rep(1/m, m))
da.learn <- da[-val,]
da.valid <- da[val,]
da.kknn <- kknn(LABEL~.,da.learn,da.valid,distance = 5,kernel= "triangular")
summary(da.kknn)
fit <- fitted(da.kknn)
table(da.valid$LABEL, fit)

结果

可能是数据比较简单，得到的结果都挺准确的。