对游戏空间进行分区降低计算复杂度

        在游戏开发中通常会将场景进行切分，最简单的用一个二维网状数据结构来表示这个切分，将游戏对象根据位置所在的切分区域存储到不同的网格中，这样我们就可以高效的定位这个对象，根据分区处理对象可以只关注当前对象所在分区和相邻的分区。

        比如说我们要对场景中的作战单位做碰撞处理，如果不进行空间分区的得话，我们就只能针对每一个作战单位和其他的所有作战单位做比较来进行处理，而且很多作战单位的相对距离很远，根本不可能产生碰撞，但在这种简单粗暴的处理方式下我们还是要对这样的作战单位进行比较计算，如果这样的作战单位很多的话无疑是对CPU周期的巨大浪费。

        如果我们对空间进行分区，然后根据作战单位所在分区把它们放到一个数组中，这样针对一个作战单位我们就可以只关注相同分区内的其它作战单位，和相邻的一半分区内的作战单位进行计算。这样可以节约很多无效的计算过程。

        空间划分后作战单位分布如下图所示:

        为了实际效果，我们不仅要处理统一分区内的作战单位，还要处理相邻分区的作战单位，就像下面这中情况:

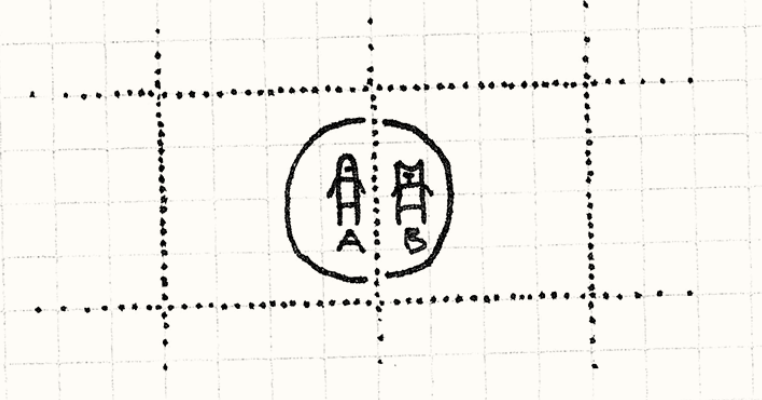
        在处理相邻分区时，我们只需要处理相邻8个分区的其中4个就可以了。这样可以避免两个相邻单元格的重复计算，就像下图所示:

         上面只是针对空间区分的高层次概括，具体的实现则要根据项目具体的需求选择合适的数据结构。比如选择四叉树作为分区的数据存储结构，如果一个分区里面的单位分布过于密集，我们可以通过添加树节点来进一步划分分区，随着游戏的进行，如果一个密集的分区在作战单位被删除一部分后变的稀疏，那么我们就可以合并这些分区。这些分区的细分和合并过程对应着四叉树的添加节点和删除节点。

        就像下面的图示:

针对具体的空间分区还有一些常见的数据结构可供选择，比如下面这些：

1. 网格[Grid（spatial_index）]

2. 二叉空间分割

3. k-dimensional树

4. 层次包围盒

每一个空间数据结构基本都是从一个现有已知的一维数据结构扩展到多维，了解它们的线性结构会帮助你判断它们是否适合于解决你的问题：

1. 网格是一个连续的桶排序

2. 二叉空间分割，k-d树，以及层次包围盒都是二叉查找树

3. 四叉树和八叉树都是Trie树

参考: Spatial Partition · Optimization Patterns · Game Programming Patterns