【粒子跟踪】结合在线贝叶斯和窗口化背景及信号定位估计，有助于在复杂环境中进行主动反馈粒子跟踪-优快云博客

简介

方法

卡尔曼滤波（Kalman）

结合在线贝叶斯和窗口估计背景与信号 (COBWEBS)

在线贝叶斯估计（Online Bayesian Estimation）

窗口化的信号与背景估计（Windowed Estimation of Signal and Background）

摘要：尽管主动反馈单颗粒方法（active-feedback single-particle methods）能在体外（in vitro）成功跟踪单个分子，但将其扩展到在活细胞中跟踪快速扩散和未被限制的蛋白质尚未实现。由于现有的主动反馈定位方法（active-feedback localization methods）在假设零背景的情况下实时定位颗粒，因此它们不适合在活细胞的不均匀背景环境中进行跟踪。在这里，我们开发了一种基于近期数据的信号和背景水平的窗口估计，用于估算当前颗粒亮度和背景强度。这些估计有助于递归贝叶斯位置估计，改进了当前基于卡尔曼滤波的定位方法。结合在线贝叶斯和背景信号的窗口估计（COBWEBS）超过了现有的二维定位方法。模拟结果表明，在均匀背景下，对于选定的颗粒和背景强度组合，其定位精度和响应性得到了改善。COBWEBS跟踪的改进或类似性能扩展到探讨的大多数信号和背景组合。此外，在多个颗粒强度、扩散速度和背景模式下，在不均匀背景环境中展示了更长的跟踪持续时间。COBWEBS能够在高且不均匀的背景下准确跟踪颗粒，包括颗粒强度变化高达三倍的情况，使其成为推动活性反馈单荧光分子跟踪以深入细胞的首选方案。

主动反馈（Active Feedback）是一种控制机制，它通过实时监测系统输出，并根据监测结果动态调整系统输入，以实现特定的控制目标。这种机制在许多领域都有广泛应用，尤其是在需要精确控制和实时调整的系统中。

主动反馈单颗粒方法（Active-Feedback Single-Particle Methods）是单粒子跟踪（single-particle tracking（SPT））中用于连续监测和实时控制单个粒子位置的先进技术。是具有高精度和时间分辨率的跟踪单个粒子的强大工具集，为在单分子水平上研究动态过程提供了显著的优势。

主动反馈颗粒跟踪显微镜适用于日益增多的关键生物和化学研究问题。尽管在体外成功跟踪单一染料标记的分子和活细胞中的更亮颗粒，但这些强大方法的扩展以跟踪活细胞中快速扩散和无约束的蛋白质尚未实现。四面体方法已应用于甘油/水溶液中的单一荧光染料和荧光蛋白，以及活细胞中的膜结合或囊泡限制的量子点（亮）标记的蛋白质。轨道追踪已被应用于研究脊椎动物轴突上的线粒体运输和人工病毒在微管中的运输，这两者都是带有许多荧光标记的亮颗粒。

简介

至今，主动反馈跟踪实验依赖于相对简单的算法来估计粒子位置。这种简单性是必要的，因为分子必须被定位，并在分子有机会扩散出检测体积之前及时应用反馈，这大约是在毫秒级的时间尺度上。算法复杂性的增加会导致位置估计计算时间的增加，从而限制响应能力。为了保持估计计算时间低于物理响应速度，大多数跟踪实现使用强度变化来检测粒子位置的变化。

三维单分子主动实时追踪（3D single-molecule active real-time tracking（3D-SMART））方法使用假设的高斯递归估计来定位粒子，这种方法假设背景光子数量为零，并且更重视最近到达的光子（权重更高）。虽然这种方法在低背景环境下表现良好，但在存在强烈且不均匀背景的环境中，零背景假设会导致粒子位置估计的偏差。

假设的高斯递归估计（Assumed Gaussian recursive estimation）：

这是一种基于高斯分布假设的递归估计方法。在3D-SMART中，粒子的位置是通过递归地更新粒子位置的概率分布来估计的。这种方法假设粒子位置的概率分布是高斯分布，并且最近到达的光子对位置估计的贡献更大。

权重更高的是最近到达的光子（Weights more recent photon arrivals more heavily）：

在递归估计中，最近到达的光子被认为对粒子位置的估计更有价值，因此给予更高的权重。这意味着粒子位置的估计更倾向于最近检测到的光子位置。

零背景假设（Zero-background assumption）：

现有的3D-SMART方法假设背景光子（即不是来自目标粒子的光子）的数量为零。这个假设在低背景环境下是合理的，但在存在强烈且不均匀背景的环境中，这个假设会导致粒子位置估计的偏差。

在这项工作中，我们展示了一种新颖的窗口信号和背景估计算法，以改善 XY 平面中的定位。利用最新光子的一部分，我们估计了被追踪粒子及其环境的强度。这些信号和背景估计通过递归贝叶斯算法促进了位置的估计。联合在线贝叶斯方法和窗口估计（online Bayesian and windowed estimation of background and signal (COBWEBS)）能够在高且不均匀背景存在的情况下准确追踪粒子。这里介绍的 COBWEBS 算法对剧烈突变的信噪比（signal-to-background ratios）具有鲁棒性，利于其促进主动反馈单荧光基团跟踪到细胞内部。

窗口信号和背景估计算法（Windowed signal and background estimation algorithm）：

通过使用最近一段时间内的光子数据（即窗口数据）来估计粒子的信号强度和背景强度。这种方法可以动态调整信号和背景的估计值，以适应环境的变化。

递归贝叶斯算法（Recursive Bayesian algorithm）：

用于更新粒子位置的概率分布。它结合了先验概率（基于之前的估计）和新的观测数据（即光子到达的位置），以计算后验概率分布，从而得到粒子的当前位置估计。

信噪比（Signal-to-background ratios）：

信号强度与背景强度的比值。在粒子跟踪中，高信噪比意味着粒子的信号比背景噪声更强，这有助于更准确地定位粒子。

方法

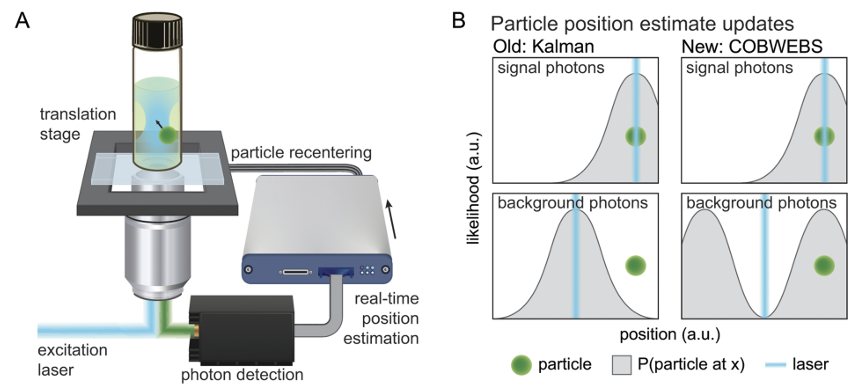
(A) 主动反馈单粒子追踪的一般示意图。激发激光（excitation laser）在搜索模式中进行扫描。荧光光子被过滤并检测到。计数的光子及其到达位置用于计算粒子位置的估计。然后，将位置估计输入平移台（translation stage），该平台被移动以将追踪到的粒子重新居中于搜索区域中。

Translation Stage（平移台）：用于精确移动样品，以确保粒子保持在激光束的焦点内。

Particle Recentering（粒子重中心）：指通过反馈机制将粒子重新定位到激光束的中心。

Excitation Laser（激发激光）：用于激发粒子，使其发出可检测的荧光信号。

Photon Detection（光子检测）：检测由粒子发出的荧光光子。

Real-time Position Estimation（实时位置估计）：利用检测到的光子信息，实时估计粒子的位置。

(B) 在光子检测后的估计更新步骤中使用的粒子位置概率分布，包括传统的Kalman方法和新的COBWEBS方法。

Kalman 方法：

Signal Photons（信号光子）：假设所有检测到的光子都来自粒子本身（信号光子），并忽略背景光子的影响。

Background Photons（背景光子）：未考虑背景光子的影响，即使在存在背景光子的情况下，也只考虑信号光子来更新粒子位置的概率分布（P(particle at x)）。

COBWEBS 方法：

Signal Photons（信号光子）：同样考虑信号光子，但同时考虑背景光子的影响。

Background Photons（背景光子）：在更新粒子位置的概率分布时，同时考虑信号光子和背景光子的影响。

Improved Position Estimation（改进的位置估计）：通过同时考虑信号光子和背景光子，COBWEBS能够更准确地估计粒子的位置，特别是在存在强烈且不均匀背景的情况下。

卡尔曼滤波（Kalman）

假设的高斯密度滤波器（Gaussian density filter）映射到适合位置估计的卡尔曼滤波器的推导包含了几个假设。系统的点扩散函数（point spread function（PSF））假设为对称高斯函数。此外，激光点的协方差（laser spot covariance） $W$ 假设为对角形式，只要光束的不对称性（beam asymmetry）与反馈施加的轴相同，这种情况就成立。

高斯密度滤波器（Gaussian density filter）：
一种假设所有概率分布都是高斯分布（正态分布）的滤波器。通过这种假设，可以使用均值和方差来描述概率分布，从而简化计算。

点扩散函数（Point Spread Function, PSF）：
描述光学系统对一个点光源的成像能力。在这里，假设PSF是一个对称的高斯函数，也就是说，光学系统将一个点光源成像为一个高斯分布的光斑。

激光斑协方差（Laser spot covariance, W）：
描述激光斑的形状和大小的统计特性。假设W是对角矩阵，意味着激光斑的不对称性（如果有的话）只沿着反馈所应用的轴方向。

有两个主要假设允许将所有似然值建模为高斯分布。

首先，假设背景水平为零。在实践中，这意味着所有检测到的光子都来自被跟踪的分子，没有背景噪声。这在背景信号非常低的环境中通常是成立的。
其次，假设激光扫描的速度比光子检测的速率快得多。这意味着在扫描的一个时间间隔（bin time，指的是用于位置估计的时间窗口）内，最多只会检测到一个光子。

方程（1）（2）：在上述假设之后，假设的高斯密度滤波器的更新方程简化为方程（1）和（2），当前粒子位置是激光协方差 $W$ 、检测到的光子数n和与之前位置估计相关的方差σ²的函数;

方程（3）（4）：在位置估计过程中，粒子和平移台可以被视为静止的。这是因为它们的位移非常小（它们的步长（step sizes）比激光扫描区域米小几个数量级），可以忽略不计。这简化了卡尔曼滤波器的预测步骤到方程（3）和（4）。该模型假设是各向同性的随机扩散（isotropic random diffusion）。

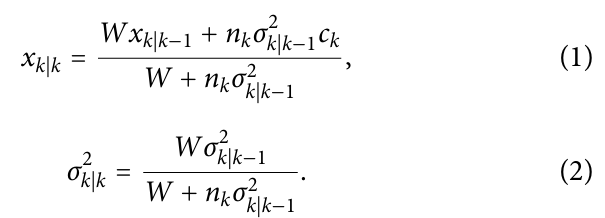
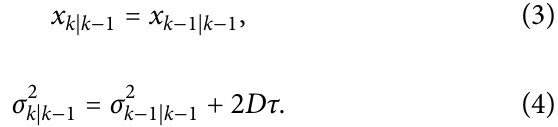
下标k和k-1分别为当前间隔或之前间隔赋值。通过假设的高斯位置估计计算的均值给出的位置信息为x。激光点中心位置为c；D 是扩散系数， $\tau$ 是给定估计的时间间隔。

扩散系数（Diffusion coefficient, D）：

描述粒子在介质中扩散速率的参数。这里的粒子扩散系数大约为1~10μm²/秒。

各向同性随机扩散（Isotropic random diffusion）：

假设粒子在所有方向上的扩散是均匀的，没有特定的偏好方向。

估计的粒子位置 $x_k$ 被输入到一个比例-积分-微分 (proportional-integral-derivative（PID）) 反馈控制器（公式 $u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) \, d\tau + K_d \frac{de(t)}{dt}$ ）中，该控制器驱动反馈跟踪方法的响应机制并重新定位粒子。这种卡尔曼滤波器在低背景环境下对 3D-SMART 的效果非常好，但内置的零背景假设对于在现实环境中的跟踪具有显著影响。

比例-积分-微分（Proportional-Integral-Derivative, PID）控制器

通过计算控制对象的误差（即期望值与实际输出值之间的差异），然后根据这个误差来调整控制信号。

比例（P）：
比例项直接与当前误差成比例。比例增益（Kp）决定了误差对控制信号的影响程度。比例项可以快速响应误差，减小稳态误差。

积分（I）：
积分项与误差随时间的积分成正比。积分增益（Ki）决定了过去误差对当前控制信号的影响。积分项有助于消除稳态误差，提高系统的稳定性。

微分（D）：
微分项与误差变化率成正比。微分增益（Kd）决定了误差变化速度对控制信号的影响。微分项可以预测误差的未来趋势，提高系统的响应速度，减少超调。

结合在线贝叶斯和窗口估计背景与信号 (COBWEBS)

在线贝叶斯估计（Online Bayesian Estimation）

在线贝叶斯估计是一种动态更新粒子位置的方法，它利用贝叶斯推断来结合先验知识和新的观测数据，从而实时更新粒子位置的概率分布。

先验概率（Prior Probability）：基于之前的观测数据，对粒子位置的初始估计。

似然函数（Likelihood Function）：根据新的观测数据（如光子到达的位置）计算粒子位置的概率。

后验概率（Posterior Probability）：结合先验概率和似然函数，计算出粒子位置的更新估计。

递归更新：每次接收到新的光子数据时，后验概率成为下一次更新的先验概率，从而实现动态更新。

为了开发一个可以考虑非零和非均匀背景的位置信估计算法，我们应用递归贝叶斯推断，并去除所有似然可以近似为高斯分布的假设。假设激光激发功率低于饱和（saturation），给定区间内的预期光子检测速率 $\gamma _k$ 可以建模为粒子与激光点之间距离的高斯函数，加上背景发射率（background emission rate）。

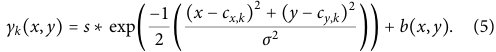
这里， $c_k$ 是给定区间的激光点中心位置，s是给定区间的最大发射器（信号）计数率，b(x,y)是非发射器（背景）计数率。假设协方差矩阵是对角的，类似于上述的卡尔曼情况，这个计算变成了公式(5)，其中σ是点扩散函数（PSF）的宽度，x和y是粒子在给定轴上的位置。

递归贝叶斯推断（Recursive Bayesian Inference）：

一种动态更新粒子位置的方法，通过结合先验知识和新的观测数据，实时更新粒子位置的概率分布。

贝叶斯推断利用贝叶斯定理，结合先验概率和似然函数来计算后验概率。

光子检测速率（Photon Detection Rate）：

光子检测速率 $\gamma _k$ 是一个关键参数，表示在给定时间间隔内预期检测到的光子数。

光子检测速率可以建模为高斯函数，描述了粒子与激光光斑之间的距离对检测速率的影响。

激光光斑中心位置（Laser Spot Center Position, $c_k$ ）：

激光光斑在每个时间间隔内的中心位置。

信号光子计数速率（Signal Photon Count Rate, s）：

信号光子的最大计数速率，以每秒计数（cps）为单位。

背景光子计数速率（Background Photon Count Rate, b(x,y)）：

背景光子的计数速率，以每秒计数（cps）为单位，并且是位置的函数，因为背景是空间依赖的。

点扩散函数宽度（Width of the Point Spread Function, σ）：

描述光学系统对一个点光源的成像能力（粒子发出的光的扩散情况），通常用高斯函数的宽度来表示。

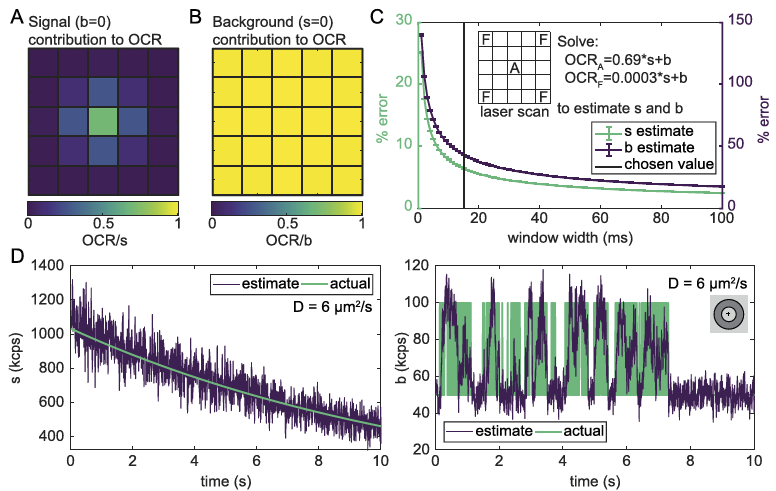
在时间区间 $\tau$ 内检测到 n 光子的概率由泊松分布给出，如下所示：

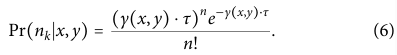
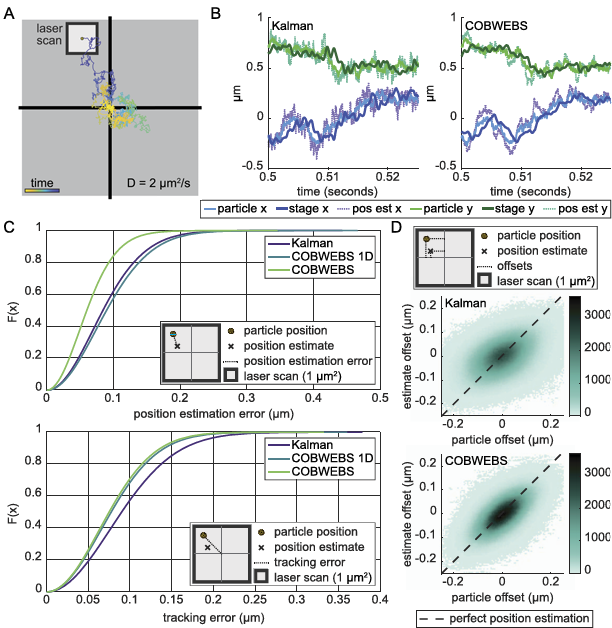
更新步骤结合了在位置 ( $x_k, y_k$ ) 处检测到 n 个光子的概率与在该位置找到粒子的先验概率。我们有

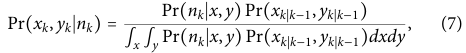
其中 $P_r(x_k,y_k|n_k)$ 是归一化的后验似然分布， $P_r(x_{k|k-1},y_{k|k-1})$ 是给定所有先前观测值的先验似然分布。

后验分布的最大值提供当前粒子位置的最大似然估计（maximum-likelihood estimate（MLE））。在跟踪中，这个 MLE 被输入到一个比例-积分-微分（PID）反馈控制器中。

对于一个静止的粒子，这个后验分布将成为下一个观测时间间隔的先验分布，过程将不断重复。
对于一个移动的粒子，必须考虑由于粒子运动引入的位置的不确定性。在这里，使用了数值卷积方法，将预期的扩散核（描述粒子扩散的数学模型）与当前的后验概率分布（公式（7））相结合。这个卷积的输出然后成为下一个观测箱的先验分布，过程将不断重复。

扩散核（Diffusion Kernel）：

描述粒子因扩散而移动的数学模型。它表示粒子在给定时间内可能移动的位置的概率分布。

在以下的仿真中，这种递归贝叶斯定位的解析形式被转换为数值实现。此外，还开发了计算简化方法，以提高计算速度并确保COBWEBS定位通过FPGA的最终实验实现的合理性。通过假设粒子位置在X轴和Y轴上的概率分布完全独立，开发了一种计算上简化的贝叶斯实现COBWEBS，即COBWEBS-1D。假设的独立性将先验和后验分布中的元素数量从V²减少到2V，其中V是沿给定坐标轴的元素数量（假设网格间距相等）。

窗口化的信号与背景估计（Windowed Estimation of Signal and Background）

窗口化的信号与背景估计是一种方法，通过使用最近一段时间内的光子数据（即窗口数据）来估计粒子的信号强度和背景强度。这种方法可以动态调整信号和背景的估计值，以适应环境的变化。

滑动窗口（Sliding Window）：选择最近一段时间内的光子数据作为当前估计的基础。窗口的大小可以根据需要调整，以平衡响应速度和估计精度。

信号估计（Signal Estimation）：通过分析窗口内的光子数据，估计粒子的信号强度。信号强度通常与粒子的亮度相关。

背景估计（Background Estimation）：同时估计背景光子的强度。背景光子可能来自样品的自荧光或其他非特异性信号。

动态调整：随着新的光子数据不断到来，窗口内的数据不断更新，从而实现信号和背景估计的动态调整。

上述所述的贝叶斯位置估计需要粒子信号（s）和背景（b）的知识（公式 (5)）。先验选择 s 和 b值（即预先设定了s和b的值）会导致以下问题：

引入潜在的粒子选择偏差。只有那些信号强度和背景强度接近这些预设值的粒子才会被准确地识别和跟踪，而忽略了其他可能重要的粒子（例如，如果某个粒子的信号强度明显低于预设的s值，那么它可能不会被系统有效地检测或跟踪）
妨碍对变化强度的响应。在实验过程中，粒子的信号强度可能会发生变化，例如由于光漂白（photobleaching）导致信号强度逐渐减弱，或者粒子在更亮的背景物体附近扩散，导致背景强度变化。如果s和b的值是预先设定且固定的，那么系统可能无法及时响应这些变化。

因此，在线估计 s 和 b 是至关重要的。3D-SMART 中的激光扫描使用 5 × 5 骑士巡游模式，覆盖一个 1 微米的正方形。由于扫描区域大于粒子的点扩散函数（PSF）（σ = 0.15 微米），并且轨迹良好的粒子保持在扫描中心附近，因此从实际粒子发出的观察信号的比例在扫描区域内变化。

变量s和b的贡献使得可以从给定扫描位置的观察计数率（OCR）中估计s和b值。由于光子到达具有随机性，OCR是在一个滑动窗口内计算的，这个窗口使用最新的光子数据，以适应随时间变化的条件，从而动态估计s和b的值。OCR还可以在整个扫描区域内进行计算，并用于定义给定s值的最大可观察粒子强度。

5 × 5 骑士巡游模式（5 × 5 knights tour pattern）：

在国际象棋中，骑士每次移动都是先沿直线走两格，然后转90度走一格，或者先转90度走一格，再沿直线走两格，形成一个"L"形的移动路径。

路径规划：
在5 × 5的区域内，激光按照骑士的移动方式来扫描整个区域。这种路径规划可以确保激光能够均匀地覆盖整个扫描区域，没有遗漏。

均匀覆盖：
由于骑士移动的非直线特性，这种扫描模式可以保证激光在扫描过程中对整个区域进行均匀的覆盖，这对于荧光显微镜等应用中的成像质量非常重要。

避免重叠：
骑士巡游模式的设计避免了激光在扫描过程中的重叠，确保每个点只被扫描一次，从而减少信号的重叠和干扰。

观察计数率（observed count rate, OCR）：

OCR是指在特定位置和时间间隔内检测到的光子数量。它受信号强度（s）和背景强度（b）的影响。在扫描区域内，信号强度（s）和背景强度（b）对OCR的贡献是变化的。通过分析不同位置的OCR，可以解算出s和b的估计值。

(A) 在b = 0时，OCR与输入s值比率在一系列s值上的比率（500次试验，每次100毫秒）。

(B) 在s = 0时，OCR与输入b值的比率。

(D) 对于一个跟踪的扩散粒子，随时间变化的s和b的估计值（基于COBWEBS）与实际值的对比。（最大持续时间10秒，扩散系数D = 6 μm²/s，衰减常数 = 1.6094 × 10⁻⁶）

结果

信号和背景估计

在完整算法实施之前，需要确定每个像素的OCR对真实s和b值的依赖关系。在典型跟踪实验中，平移台/激光扫描的中心与实际粒子位置之间的偏差被近似为标准差为0.1μm的正态分布。根据该校准分布生成伪随机粒子位置，然后为一系列信号和背景值生成光子。在零背景的情况下，对一系列信号值的试验[图2(A)]以及相反的情况[图2(B)]被用来建立真实s和b值与给定像素类型的OCR之间的关系。对于s和b值组合，其中两个值均为非零，角落像素F的OCR被发现为0.0003s+b。中心像素A的OCR为0.69s+b。这些表达式形成了一个可解的线性方程组，用于从OCR中提取s和b的估计值（图2）。这个A和F像素对被发现是从六种可用像素类型中用于信号和背景估计的最准确组合。

六种可用像素类型是基于5×5骑士巡游扫描模式中的不同位置定义的，包括中心像素（A）、边缘中心像素（B、C、D、E）和角落像素（F）

接下来，确定从OCR（观察计数率）中提取信号强度（s）和背景强度（b）值的时间窗口大小。使用相同的校准分布，研究人员将用于确定OCR的时间窗口从1毫秒到100毫秒不等，以观察不同窗口大小对s和b估计的影响。较大的时间窗口可以提高s和b估计的准确性，因为它们包含了更多的数据点，从而减少了随机波动的影响。[图2(C)]。选择了使用最近15毫秒的数据来计算OCR，用于后续的模拟。尽管使用超过15毫秒的窗口可以进一步将s和b估计的百分比误差减少大约一半[图2(c)]，但这会降低估计对环境变化的响应能力。（较大的时间窗口虽然提高了准确性，但可能无法及时捕捉到信号或背景的快速变化。）

校准分布（Calibration Distribution）：

用于模拟和测试估计方法的标准数据分布，帮助确定最佳的时间窗口大小。

时间窗口是指用于计算OCR的最近一段时间的数据。这个窗口的大小会影响s和b估计的准确性和响应能力。

最后，利用实际的COBWEBS跟踪数据来探索对动态变化的s和b的估计响应能力 [图2(D)]。随着真实信号值以指数方式下降，模拟光漂白过程，COBWEBS追踪的粒子的估计s值随着真实值的下降而下降 [图2(D)]。这表明COBWEBS能够有效响应信号强度的变化。空间依赖的背景遵循与后续实验相同的“甜甜圈”模式。背景估计随着轨迹过程中真实背景水平的变化而变化，并在与背景界面（background interface）的活跃交互时采取中间值。具有2 μm²/s扩散速度的动态变化粒子强度通常会系统性地高估真实值。而具有6 μm²/s扩散速度的动态变化粒子强度则显示出更好的估计。这是因为更快扩散的粒子的实际位置与用于定义WEBS方程的校准分布（即用于定义WEBS方程的预先确定的数据分布，帮助估计s和b的值）之间的吻合更好。

光漂白（Photobleaching）：荧光分子因光照射而逐渐失去荧光发射能力的现象。

甜甜圈模式（Donut pattern）：描述背景强度在空间上的分布模式，可能呈现中心低、周围高的环形分布。

背景界面（Background interface）：指粒子在不同背景强度区域之间的边界或过渡区域。

在均匀背景环境中的粒子追踪

对Kalman和COBWEBS跟踪性能的比较算法使用两种类型的误差：

跟踪误差（Tracking error）是颗粒位置与平台位置之间的偏差。这测量了颗粒在跟踪过程中的集中程度。
位置估计误差（Position estimation error）是估计的颗粒位置与颗粒真实位置之间的差异。这测量了颗粒位置计算的准确性。

这些误差分别通过方程（8）和（9）计算。 $Stg$ 是给定轴上的平台位置， $P$ 是给定轴上的颗粒位置， $P_{Est}$ 表示给定轴上的估计位置。此外，图3(C)中的插图形象地定义了相同的方程。

(A) 在均匀背景下跟踪的示意图。

(B) Kalman 和 COBWEBS 跟踪示例轨迹的片段，显示实际粒子位置、估计粒子位置以及由此产生的模拟阶段响应。

(D) 粒子位置估计偏差与物理粒子偏差的二维直方图。Kalman 和 2D 贝叶斯估计的相关系数分别为 0.4501 和 0.6325.

在非均匀背景环境中的粒子追踪

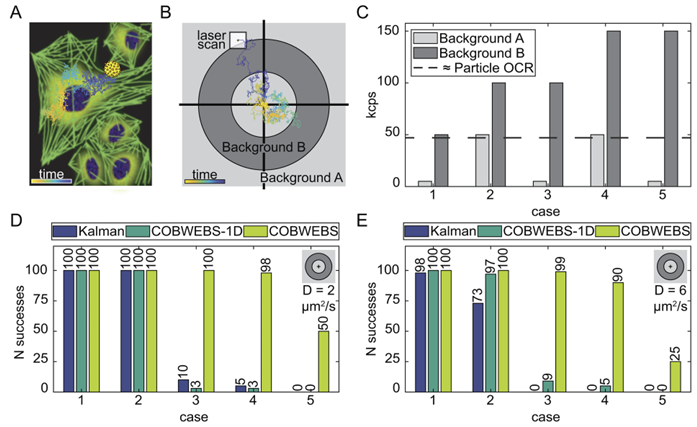
（A）病毒扩散轨迹的卡通图叠加在荧光标记细胞的图上。

（B）包含两个不同背景界面的甜甜圈结构背景的图（位于初始粒子位置的2和4微米处）。白色框是激光扫描的大小。

径向对称的甜甜圈背景（donut structured background）图案：

使得能够在10秒扩散轨迹中模拟与背景水平的高低界面的持续互动。使用仅包含一个1.5微米界面简化的点图案来探索额外的案例。扩散颗粒通常在模拟轨迹中穿越每个背景界面100次，并且每个界面至少可靠地穿越一次。

（C）用于跟踪模拟的高背景和低背景水平。条形的颜色对应于（B）中描绘的每个背景水平的位置。例如，在案例1中，背景从5 k开始，然后增加到50 k。案例按跳跃大小递增组织，其次按初始背景水平组织。

（D）甜甜圈背景模式的跟踪成功率。N成功是指在整个可能的轨迹持续时间内，粒子保持在激光扫描边缘0.5微米范围内的轨迹总数（100次试验，最大持续时间10秒，s = 516.64 kcps，D = 2 μm²/s）。

（E）快速甜甜圈成功计数（100次试验，最大持续时间10秒，s = 516.64 kcps，D = 6 μm²/s）。

探讨

COBWEBS位置估计显著提高了在模拟轨迹中对非均匀背景的跟踪稳健性。COBWEBS方法通过改进位置估计，减少了位置估计误差和跟踪误差，适用于大多数粒子和背景强度组合。因为由于后处理数据的计算复杂性，平台位置通常用作粒子位置。

扩展了跟踪可能的背景范围：COBWEBS有可能扩展对于足够亮的粒子可跟踪的背景水平范围。
对扩散速度的不变性：相较于Kalman位置估计，COBWEBS对于可跟踪和不可跟踪粒子的区分对扩散速度更具有不变性，表明了改进的一致性。
延长了轨迹持续时间：COBWEBS显著增加了在非均匀背景环境中自由扩散粒子的可能轨迹持续时间，这对应于活细胞的环境。
对扩散系数的鲁棒性：COBWEBS的位置估计对扩散系数的高估比Kalman位置估计更具弹性。

在实现 COBWEBS 跟踪的实验优势之前，必须将其转换为 FPGA。可能遇到以下问题：

FPGA的计算资源限制：FPGA在执行复杂数学运算（如乘法和除法）时计算资源有限。因此，需要将COBWEBS算法转换为适合FPGA执行的形式。
数值卷积的障碍：必须在实空间中执行数值卷积，用于考虑粒子扩散的影响。

这些优化措施将COBWEBS估计简化为包含最少复杂操作的过程：

对数空间转换：将所有概率分布转换为对数空间，可以将几乎所有的乘法和除法运算转换为加法和减法运算。这显著降低了COBWEBS估计的计算复杂度。
查找表的使用：对数空间和实空间之间的转换可以通过查找表（look-up tables）来实现。同样，方程（6）中的阶乘运算也可以通过查找表来处理。
部分γk的存储：方程（5）中的指数项γk仅依赖于激光扫描位置和粒子位置。可以为每个可能的激光位置预先计算并存储这部分γk值，从而将给定位置像素的预期计数率计算简化为通过 sEst⋅（k）和 bEst⋅（k）的单次乘法和加法运算。
减少网格采样：进一步减少网格采样可以减少每个估计计算的总元素数量和扩散核的大小。

总结

COBWEBS将在线贝叶斯估计和窗口化的信号与背景估计结合起来，以提高粒子位置估计的准确性和鲁棒性。具体来说，COBWEBS通过以下步骤实现：

信号和背景估计：
使用窗口化的信号与背景估计算法，实时估计粒子的信号强度和背景强度。这些估计值基于最近一段时间内的光子数据，能够动态适应环境的变化。
贝叶斯位置估计：
利用在线贝叶斯估计，结合信号和背景估计值，更新粒子位置的概率分布。通过贝叶斯推断，结合先验概率和新的观测数据，计算出粒子位置的后验概率分布。
动态更新：
每次接收到新的光子数据时，更新信号和背景估计值，并重新计算粒子位置的后验概率分布。这种动态更新机制确保了粒子位置估计的实时性和准确性。
鲁棒性：
COBWEBS对剧烈变化的信噪比具有鲁棒性，能够在高背景和非均匀背景环境中准确追踪粒子。即使在背景强度变化较大的情况下，也能保持稳定的跟踪性能。

参考文献：

Combined online Bayesian and windowed estimation of background and signal localization facilitates active-feedback particle tracking in complex environments (2022)