支持向量机（SVM）

SVM简介

SVM，Support Vector Machine，它是一种二分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

这里涉及了几个概念，二分类模型，线性分类器，间隔最大化，凸二次规划问题。

• 二分类模型：给定的各个样本数据分别属于两个类之一，而目标是确定新数据点将归属到哪个类中。
• 线性分类器：分割样本点的分类器是一个超平面，这也就要求样本线性可分，这是hard-margin SVM的要求，对于后来的soft-margin SVM，放低为近似线性可分，再到后来的核技巧，要求映射到高维空间后要近似线性可分。
• 线性可分：$D0$和$D1$是$n$维欧氏空间中的两个点集（点的集合）。如果存在 $n$维向量 $w$和实数$b$，使得所有属于$D0$的点 xi 都有 $w{x}_i+b>0$，而对于所有属于$D1$的点 $x_j$则有 $w{x}_j+b<0$。则我们称$D0$和$D1$线性可分。
• 间隔最大化：首先要知道SVM中有函数间隔和几何间隔，函数间隔刻画样本点到超平面的相对距离，几何间隔刻画的是样本点到超平面的绝对距离，SVM的直观目的就是找到最小函数距离的样本点，然后最大化它的几何间隔。
• 凸二次规划：目标函数是二次的，约束条件是线性的。

核心公式

• 线性可分训练集： T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{n}, y_{n}\right)\right\} T={ (x1​,y1​),(x2​,y2​),…,(xn​,yn​)}
• 学习得到的超平面：$w^{\ast T}x+b^{\ast }=0$
• 相应的分类决策函数：$f(x)=\mathrm{sign}\left(w^{\ast T}x+b^{\ast }\right)$
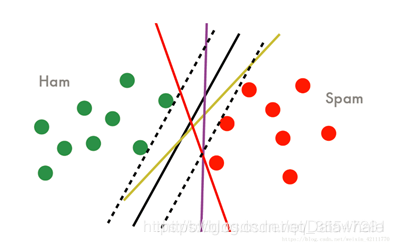
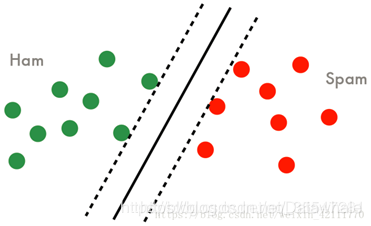
• SVM基本思想：间隔最大化，不仅要讲正负类样本分开，而且对最难分的点（离超平面最近的点）也要有足够大的确信度将他们分开。
  
  

函数间隔

给定一个超平面$(w,b)$，定义该超平面关于样本点 $(x_i,y_i)$ 的函数间隔为：$$\hat{\gamma }i=yi\left(w^T{x}_i+b\right)$$ 定义该超平面关于训练集$T$的函数间隔为：$$\hat{\gamma }=\min i=1,2,\dots ,N\hat{\gamma }i$$

几何间隔

给定一个超平面$(w,b)$，定义该超平面关于样本点 $(x_i,y_i)$ 的几何间隔为：$${\gamma }_i=y_i\left(\frac{w^T}{|w|}{x}_i+\frac{b}{|w|}\right)$$ 定义该超平面关于训练集$T$的几何间隔为：$$\gamma =\min i=1,2,\dots ,N\gamma i$$

函数间隔与几何间隔的关系

$$\begin{array}{c}{\gamma }_i=\frac{{\hat{\gamma }}_i}{|w|},i=1,2,\dots ,N\gamma =\frac{\hat{\gamma }}{|w|}\end{array}$$

间隔最大化

1. 求得一个几何间隔最大的分离超平面，可以表示为如下的最优化问题：
   $$\begin{array}{c}\max w,b\gamma \text{s.t.}yi\left(\frac{w^T}{|w|}{x}_i+\frac{b}{|w|}\right)\ge \gamma ,i=1,2,\dots ,N\end{array}$$
2. 考虑函数间隔与几何间隔的关系式，改写为：
   $$\begin{array}{c}\max w,b\frac{\hat{\gamma }}{|w|}\text{s.t. }yi\left(w^T{x}_i+b\right)\ge \hat{\gamma },i=1,2,\dots ,N\end{array}$$
3. 等价与下式
   $$\begin{array}{c}\max w,b\frac{1}{|w|}\text{s.t. }1-yi\left(w^T{x}_i+b\right)\le 0,i=1,2,\dots ,N\end{array}$$
4. 注意到最大化$\frac{1}{|w|}$ 和最小化$\frac{1}{2}|w{|}^2$是等价的，故最优化问题可转化为：
   $$\begin{array}{c}\min w,b\frac{1}{2}|w{|}^2\text{s.t. }1-yi\left(w^T{x}_i+b\right)\le 0,i=1,2,\dots ,\end{array}$$