incSLAM++是3DV 2017最佳论文,源文件网址 https://sourceforge.net/p/slam-plus-plus/wiki/Home/
incSLAM++有两个创新点:
一是增量式Schur补更新。
如果delta更新是稀疏的,则采用增量式Schur补来求解非线性最小二乘问题,即增量式BA问题,会缩短计算时间。
求解不同关键帧之间的位姿和每帧上的点即求解增量式BA(解不是全局的),就是求解如下非线性最小二乘问题
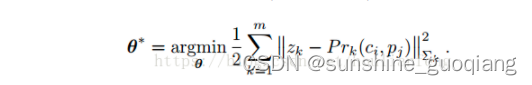
在每次迭代时,在初始点附近利用泰勒展开进行线性化,得到如下最小二乘问题
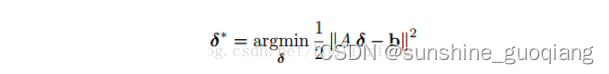
在使用最小二乘求解过程中将相机位姿和路标点分离,则LS求解的系统矩阵和右边为
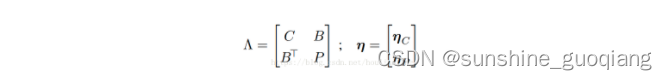
因为在线性化点附近小的改变可以忽略 所以系统矩阵用增量表达更新
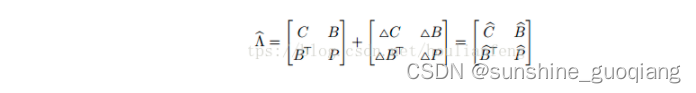
增量式Schur补变为
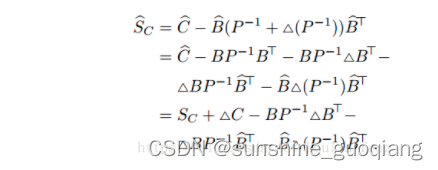
则
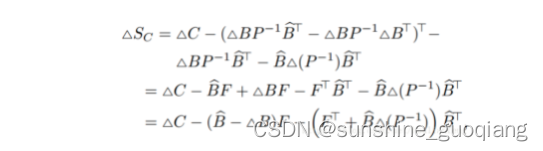
如果所有的变量都更新的话,P和deltaP-1就有同样的秩,这时问题就退化到批处理了,但是如果没有更新所有变量,当前的方法就有加速作用。
二是一种高效的协方差恢复技术。
可以使边缘协方差(marginal covariance)计算和NLS的计算时间在一个数量级上。
系统矩阵的逆就是协方差。这里采用Woodbury formula 求得了协方差,将Schur补的求逆改为Schur补的迭代。
文章强调了所提方法的优越性在于更新的稀疏性,当变量更新小于50%时候,计算代价更小。文章还采用了损失函数来削弱外点的影响。在与g2o slam++ ceres作对比的时候,g2o与slam++均采用LM solver,incSlam++与ceres均采用dogleg算法。效果对比
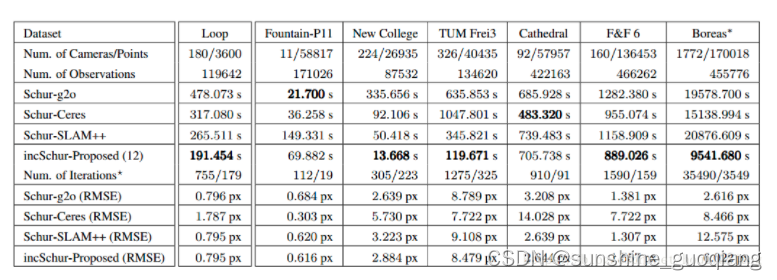





 incSLAM++是3DV2017的最佳论文,亮点在于其增量式Schur补更新加速BA求解,针对稀疏变化有效缩短计算时间。此外,文章介绍了一种高效协方差恢复技术,降低边缘协方差计算成本。文中通过与g2oSLAM++和Ceres比较,突出了稀疏性和外点抑制的优势。
incSLAM++是3DV2017的最佳论文,亮点在于其增量式Schur补更新加速BA求解,针对稀疏变化有效缩短计算时间。此外,文章介绍了一种高效协方差恢复技术,降低边缘协方差计算成本。文中通过与g2oSLAM++和Ceres比较,突出了稀疏性和外点抑制的优势。


















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










