slam后端BA优化

原创

已于 2024-03-07 10:53:53 修改 · 1.1k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#ai #机器人

于 2024-02-27 14:57:52 首次发布

博客围绕Bundle Adjustment展开，介绍了其数学模型、后端实践，包括数据集解析、最小二乘法求解等。还阐述了直接法的Bundle Adjustment，涉及数学模型和实践中的问题。此外，详细讲解了ceres库和G2o库的使用，如流程、代价函数、顶点和边的创建等。

文章目录

1、Bundle Adjustment
2、直接法的 Bundle Adjustment
3、ceres库的使用
4、G2o库的使用

1、Bundle Adjustment

参考资料：

https://www.cnblogs.com/penuel/p/13602934.html

BAL（Bundle Adjustment in large）数据集（http://grail.cs.washington.edu/projects/bal/）是⼀个⼤型 BA 数据集，它提供了相机与点初始值与观测，你可以⽤它们进⾏ Bundle Adjustment。

1.1、BA问题数学模型

1.1.1、数据集解析

数据集文件为problem-16-22106-pre.txt，数据主要包括4部分分别详细说明。

第一部分：第一行：16 22106 83718
有16个相机位姿，22106个路标点(世界坐标系下的三维坐标)，83718个观测坐标(两维像素坐标)，总体概括及时相机在16个位置下观测22106个路标点，产生83718个对应的像素坐标。每个位置只能观测到部分路标点。
第二部分：观测数据，83718个观测坐标(两维像素坐标)，共4维分别为
相机位姿编号路标点编号对应观测的像素坐标
0 0 -3.859900e+02 3.871200e+02
1 0 -3.844000e+01 4.921200e+02
2 0 -6.679200e+02 1.231100e+02
7 0 -5.991800e+02 4.079300e+02
12 0 -7.204300e+02 3.143400e+02
13 0 -1.151300e+02 5.548999e+01
0 1 3.838800e+02 -1.529999e+01
1 1 5.597500e+02 -1.061500e+02
10 1 3.531899e+02 1.649500e+02
0 2 5.915500e+02 1.364400e+02
第三部分：第一类顶点，16个相机位姿，位姿加相机内参共9维，前三维为so3(旋转向量)，接下去为t(平移向量3维), f(fx=fy=f), 去畸变参数：k1, k2。注意这里的每个位姿是相对原点的位姿，而不是相对上一个位姿的变化量。
第四部分：第二类顶点，22106路标节点的世界坐标，3维。

1.1.2、Ba问题数学描述

已知条件：相机的16个位姿点和22106个路标点(世界坐标系下的三维坐标)，这2部分参数认为是不准确的，需要优化；在图像中测量到83718个测量坐标(两维像素坐标)是准确的测量值。

最小二乘法求解问题：16个位姿点和22106个路标点(世界坐标系下的三维坐标)作为变量，已知值作为迭代的初始值，通过相机位姿和路标点世界坐标计算像素坐标，用计算的像素坐标去逼近测量到的83718个对应的像素坐标，不断迭代调整16个位姿点和22106个路标点(世界坐标系下的三维坐标)的值，使得逼近的误差最小。

最小二乘法
最小二乘法问题构建：曲线拟合，捆集调整ba。
最小二乘法求解：计算雅可比矩阵或黑塞矩阵，求解每次迭代的增量△x

1.1.3、g2o的使用步骤

创建一个线性求解器LinearSolver；
创建BlockSolver，并用上面定义的线性求解器初始化；
创建总求解器solver，并从GN/LM/DogLeg 中选一个作为迭代策略，再用上述块求
解器BlockSolver初始化；
创建图优化的核心：稀疏优化器（SparseOptimizer）；
定义图的顶点和边，并添加到SparseOptimizer中；
设置优化参数，开始执行优化

1.2、后端BA实践

1.2.1、代码实现

主要代码如下，工程代码见gitee链接: link
https://gitee.com/paul126/vslam-learn.git

#include <g2o/core/base_vertex.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/csparse/linear_solver_csparse.h>
#include <g2o/core/robust_kernel_impl.h>
#include <iostream>

#include "common.h"
#include "sophus/se3.hpp"

using namespace Sophus;
using namespace Eigen;
using namespace std;

/// 姿态和内参的结构
struct PoseAndIntrinsics {
   
   
    PoseAndIntrinsics() {
   
   }

    /// set from given data address
    explicit PoseAndIntrinsics(double *data_addr) {
   
   
        rotation = SO3d::exp(Vector3d(data_addr[0], data_addr[1], data_addr[2]));
        translation = Vector3d(data_addr[3], data_addr[4], data_addr[5]);
        focal = data_addr[6];
        k1 = data_addr[7];
        k2 = data_addr[8];
    }

    /* 将9维的估计值输出出去 */
    void set_to(double *data_addr) {
   
   
        auto r = rotation.log();
        for (int i = 0; i < 3; ++i) data_addr[i] = r[i];
        for (int i = 0; i < 3; ++i) data_addr[i + 3] = translation[i];
        data_addr[6] = focal;
        data_addr[7] = k1;
        data_addr[8] = k2;
    }

    SO3d rotation;                              /* 旋转矩阵 */
    Vector3d translation = Vector3d::Zero();    /* 平移向量 */
    double focal = 0;                           /* 相机fx=fy=f */
    double k1 = 0, k2 = 0;                      /* 去畸变参数 */
};

/* g2o本身内部定义了一些常用的顶点类型，
g2o\types\slam3d\vertex_se3.h
 class G2O_TYPES_SLAM3D_API VertexSE3 : public BaseVertex<6, Isometry3>
其他的列举出来出来为：
VertexSE2 : public BaseVertex<3, SE2>  //2D pose Vertex, (x,y,theta)
VertexSE3 : public BaseVertex<6, Isometry3>  //6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion)
VertexPointXY : public BaseVertex<2, Vector2>
VertexPointXYZ : public BaseVertex<3, Vector3>
VertexSBAPointXYZ : public BaseVertex<3, Vector3>
VertexSE3Expmap : public BaseVertex<6, SE3Quat>
VertexCam : public BaseVertex<6, SBACam>
VertexSim3Expmap : public BaseVertex<7, Sim3>

自定义顶点：重新定义顶点一般需要考虑重写如下函数：
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
// 顶点更新函数。非常重要的一个函数，主要用于优化过程中增量△x 的计算。我们根据增量方程计算出增量之后，就是通过这个函数对估计值进行调整的。
virtual void oplusImpl(const number_t* update);
// 顶点参数创建函数，创建顶点参数的空间，并将地址传递给g2o库中的 _estimate。
virtual void setToOriginImpl();    

自定义顶点需要提供2个参数：
    相机位姿参数作为顶点，共9维，前三维为so3(旋转向量)，接下去为t(平移向量3维), f(fx=fy=f), 去畸变参数：k1, k2；
    第一是顶点参数维度：9
    第二是参数的模板类型：后续会创建此类型空间，并将地址传递给 _estimate

 */

class VertexPoseAndIntrinsics : public g2o::BaseVertex<9, PoseAndIntrinsics> {
   
   
public:
    /* 此宏定义在Eigen库中定义，确保了Eigen对象能够在内存中对齐。需要对齐的原因是为了最大限速的提升运算效率，
    Eigen库的一些对象（矩阵和向量）需要特别的内存对齐，提升数学运算效率。
    在c++中使用new分配对象是不会保证这种共对齐，此宏定义可以确保new为Eigen对象分配内存是满足对齐要求。 */
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    VertexPoseAndIntrinsics() {
   
   }
    /* 创建顶点参数的结构体空间，并将地址传递给g2o库中的 _estimate  */
    virtual void setToOriginImpl() override {
   
   
        /* 这里只是显示调用构造函数，创建 PoseAndIntrinsics 结构体空间，元素并没有初始化，后面会进行初始化 */
        _estimate = PoseAndIntrinsics();
    }
    /* 顶点更新函数，我们根据增量方程计算出增量△x （对应 update）之后，此函数根据迭代的增量对估计值进行调整，是估计值更加准确 */
    virtual void oplusImpl(const double *update) override {
   
   
        _estimate.rotation = SO3d::exp(Vector3d(update[0], update[1], update[2])) * _estimate.rotation;
        _estimate.translation += Vector3d(update[3], update[4], update[5]);
        _estimate.focal += update[6];
        _estimate.k1 += update[7];
        _estimate.k2 += update[8];
    }

    /* 从函数不是g2o库要求完成的，而是根据实际需求新增的一个结构，根据估计值投影一个点 */
    Vector2d project(const Vector3d &point) {
   
   
        /* 将世界坐标转换为相机坐标 */
        Vector3d pc = _estimate.rotation * point + _estimate.translation;
        /* 相机坐标归一化平面 */
        pc = -pc / pc[2];
        /* 归一化平面的坐标去畸变的到相机的像素坐标 */
        double r2 = pc.squaredNorm();
        double distortion = 1.0 + r2 * (_estimate.k1 + _estimate.k2 * r2);
        return Vector2d(_estimate.focal * distortion * pc[0],
                        _estimate.focal * distortion * pc[1]);
    }

    virtual bool read(istream &in) {
   
   }
    virtual bool write(ostream &out) const {
   
   }
};

class VertexPoint : public g2o::BaseVertex<3, Vector3d> {
   
   
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    VertexPoint() {
   
   }

    virtual void setToOriginImpl() override {
   
   
        _estimate = Vector3d(0, 0, 0);
    }

    virtual void oplusImpl(const double *update) override {
   
   
        _estimate += Vector3d(update[0], update[1], update[2]);
    }

    virtual bool read(istream &in) {
   
   }

    virtual bool write(ostream &out) const {
   
   }
};


/* 定义边的方法
边的类型：BaseUnaryEdge，BaseBinaryEdge，BaseMultiEdge 分别表示一元边，两元边，多元边。
一元边你可以理解为一条边只连接一个顶点，两元边理解为一条边连接两个顶点，也就是我们常见的边啦，多元边理解为一条边可以连接多个（3个以上）顶点

virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
// 使用当前顶点的值计算的测量值与真实的测量值之间的误差，注意是  _error = _measurement - proj，但是 _error = _proj - measurement 也可以，只是雅可比矩阵需要对应起来。
virtual void computeError();
// 在当前顶点的值下，该误差对优化变量的偏导数，也就是我们说的Jacobian；这里不实现雅可比计算方式，g2o自己会计算，此时_error用上述2种方式都可以。
virtual void linearizeOplus();
 */
class EdgeProjection :
    public g2o::BaseBinaryEdge<2, Vector2d, VertexPoseAndIntrinsics, VertexPoint> {
   
   
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    /* 使用当前顶点的值计算的测量值与真实的测量值之间的误差 */
    virtual void computeError() override {
   
   
        auto v0 = (VertexPoseAndIntrinsics *) _vertices[0];
        auto v1 = (VertexPoint *) _vertices[1];
        /* 计算估计值二维像素坐标，根据三维的相机坐标计算二维的像素坐标 */
        auto proj = v0->project(v1->estimate());
        /* 测量值减去估计值 */
        _error = _measurement - proj;
    }

    // use numeric derivatives
    virtual bool read(istream &in) {
   
   }
    virtual bool write(ostream &out) const {
   
   }

};

void SolveBA(BALProblem &bal_problem);

int main(int argc, char **argv) {
   
   

    if (argc != 2) {
   
   
        cout << "usage: bundle_adjustment_g2o bal_data.txt" << endl;
        return 1;
    }
    /* 将problem-16-22106-pre.txt文件数据解析出来 */
    BALProblem bal_problem(argv[1]);
    bal_problem.Normalize();
    /* 给路标点坐标，相机位姿添加干扰 */
    bal_problem.Perturb(0.1, 0.5, 0.5);
    bal_problem.WriteToPLYFile("initial.ply");
    SolveBA(bal_problem);
    bal_problem.WriteToPLYFile("final.ply");

    return 0;
}

void SolveBA(BALProblem &bal_problem) {
   
   
    const int point_block_size = bal_problem.point_block_size();
    const int camera_block_size = bal_problem.camera_block_size();
    /* 路标点世界坐标地址，3维 */
    double *points = bal_problem.mutable_points();
    /* 相机参数地址，9维 */
    double *cameras = bal_problem.mutable_cameras();

    // pose dimension 9, landmark is 3
    typedef g2o::BlockSolver<g2o::BlockSolverTraits<9, 3>> BlockSolverType;

    /* 第1步：创建一个线性求解器LinearSolver */
    typedef g2o::LinearSolverCSparse<BlockSolverType::PoseMatrixType> LinearSolverType;
    /* 第2步：创建BlockSolver。并用上面定义的线性求解器初始化 */
    /* 第3步：use LM创建总求解器solver。并从GN, LM, DogLeg 中选一个，再用上述块求解器BlockSolver初始化 */
    auto solver = new g2o::OptimizationAlgorithmLevenberg(
        /* std::make_unique就是对智能指针的封装，std::unique_ptr */
        std::make_unique<BlockSolverType>(std::make_unique<LinearSolverType>()));

    /* 第4步：创建终极大boss 稀疏优化器（SparseOptimizer） */
    g2o::SparseOptimizer optimizer;     // 图模型
    optimizer.setAlgorithm(solver);     // 设置求解器
    optimizer.setVerbose(true);         // 打开调试输出

    /* build g2o problem，获取观测的像素坐标，二维变量 */
    const double *observations = bal_problem.observations();
    // vertex
    /* 第5步：定义图的顶点和边。并添加到SparseOptimizer中 */
    vector<VertexPoseAndIntrinsics *> vertex_pose_intrinsics;
    vector<VertexPoint *> vertex_points;
    for (int i = 0; i < bal_problem.num_cameras(); ++i) {
   
   
        VertexPoseAndIntrinsics *v = new VertexPoseAndIntrinsics();
        double *camera = cameras + camera_block_size * i;
        v->setId(i);
        /*   void setEstimate(const EstimateType& et) {
                _estimate = et;
                updateCache();
            } g2o\core\base_vertex.h
         */
        v->setEstimate(PoseAndIntrinsics(camera));
        optimizer.addVertex(v);
        vertex_pose_intrinsics.push_back(v);
    }
    for (int i = 0; i < bal_problem.num_points(); ++i) {
   
   
        VertexPoint *v = new VertexPoint();
        double *point = points + point_block_size * i;
        v->setId(i + bal_problem.num_cameras());
        v->setEstimate(Vector3d(point[0], point[1], point[2]));
        // g2o在BA中需要手动设置待Marg的顶点，Marginalized边缘化求解
        v->setMarginalized(true);
        optimizer.addVertex(v);
        vertex_points.push_back(v);
    }

    // edge
    /* 第5步：定义图的顶点和边。并添加到SparseOptimizer中 */
    for (int i = 0; i < bal_problem.num_observations(); ++i) {
   
   
        EdgeProjection *edge = new EdgeProjection;
        /* 设置此边连接的顶点，二元边连接2个顶点的参数：第m个相机位姿下观测第n个路标点产生的测量值保存到 _measurement 中：测量值是2维像素坐标 */
        edge->setVertex(0, vertex_pose_intrinsics[bal_problem.camera_index()[i]]);
        edge->setVertex(1, vertex_points[bal_problem.point_index()[i]]);
        edge->setMeasurement(Vector2d(observations[2 * i + 0], observations[2 * i + 1]));
        /* 信息矩阵，他是协方差矩阵之逆，在图优化中通过setInformation设置信息矩阵对边加权，也就是对改变在总体优化问题的重要性进行加权。
        Matrix2d::Identity()是一个2*2的单位矩阵，意味着该约束的所有维度都具有相同的权重 */
        edge->setInformation(Matrix2d::Identity());
        edge->setRobustKernel(new g2o::RobustKernelHuber());
        optimizer.addEdge(edge);
    }
    /* 第6步：设置优化参数，开始执行优化 */
    optimizer.initializeOptimization();
    /* 两个入参：第一个是 iterations 设置优化过程的最大迭代次数，当迭代次数达到指定最大迭代次数或达到收敛条件则退出迭代。
        第二个参数是 online 表示是否在线优化，在线优化通常用于实时系统中，意味着在优化过程中可以实时的向图中添加新的顶点和边，
            在每次迭代后都会增量式更新图的结构，以便立即处理新的顶点和边。
            我们使用时 online 一般默认为false，一次性将顶点和边添加完成后再进行求解。
    g2o\core\sparse_optimizer.h：int optimize(int iterations, bool online = false);
    g2o\core\sparse_optimizer.cpp：int SparseOptimizer::optimize(int iterations, bool online) */
    optimizer.optimize(40);

    /* 将迭代求解优化之后的参数更新到 cameras 的空间 */
    for (int i = 0; i < bal_problem.num_cameras(); ++i) {
   
   
        double *camera = cameras + camera_block_size * i;
        auto vertex = vertex_pose_intrinsics[i];
        auto estimate = vertex->estimate();
        estimate.set_to(camera);
    }
    for (int i = 0; i < bal_problem.num_points(); ++i) {
   
   
        double *point = points + point_block_size * i;
        auto vertex = vertex_points[i];
        for (int k = 0; k < 3; ++k) point[k] = vertex->estimate()[k];
    }
}

1.2.2、Meshlab安装

添加第三方软件源
sudo add-apt-repository ppa:zarquon42/meshlab
有时候会需要update一下
sudo apt-get update
安装MeshLab
sudo apt-get install meshlab
卸载MeshLab
sudo apt-get remove meshlab
删除添加的第三方软件源，在 Ubuntu Linux 中移除或删除 PPA
sudo apt-get install ppa-purge /* 安装ppa管理的工具 */
sudo ppa-purge ppa:zarquon42/meshlab

PPA，英文全称为 Personal Package Archives，即个人软件包档案。是 Ubuntu Launchpad 网站提供的一项源服务，允许个人用户上传软件源代码，通过 Launchpad 进行编译并发布为二进制软件包，作为 apt / 新立得（Synaptic）源供其他用户下载和更新。

1.2.3、测试结果

执行命令：xb@ukylin:~/learn/practice/p7-ba/build/bin$ ./ba_g2o problem-16-22106-pre.txt
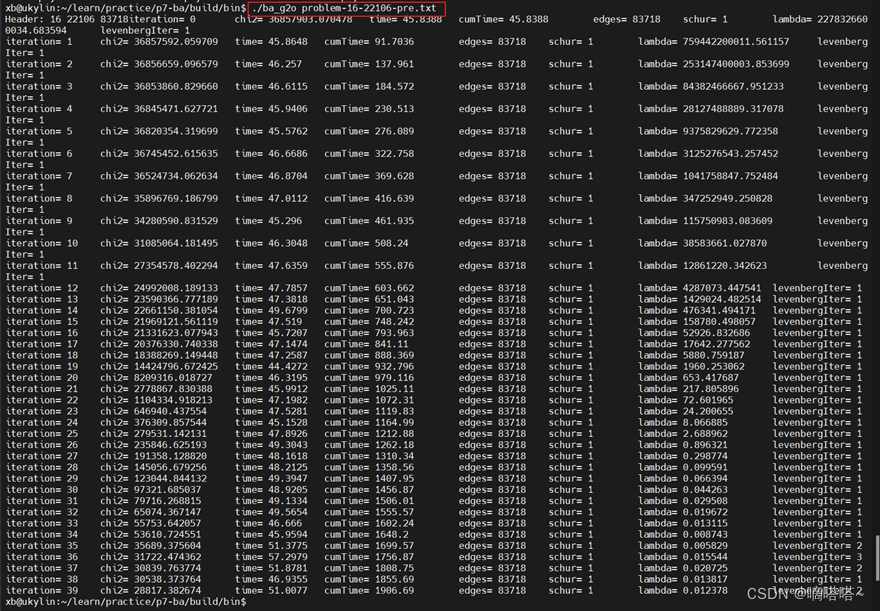
在这里插入图片描述
生成点云文件（相机16个位姿的世界坐标以及22106个路标点的世界坐标，三维）：

使用mashlab可视化点云文件
xb@ukylin:~/learn/practice/p7-ba/build/bin$ meshlab initial.ply
xb@ukylin:~/learn/practice/p7-ba/build/bin$ meshlab final.ply
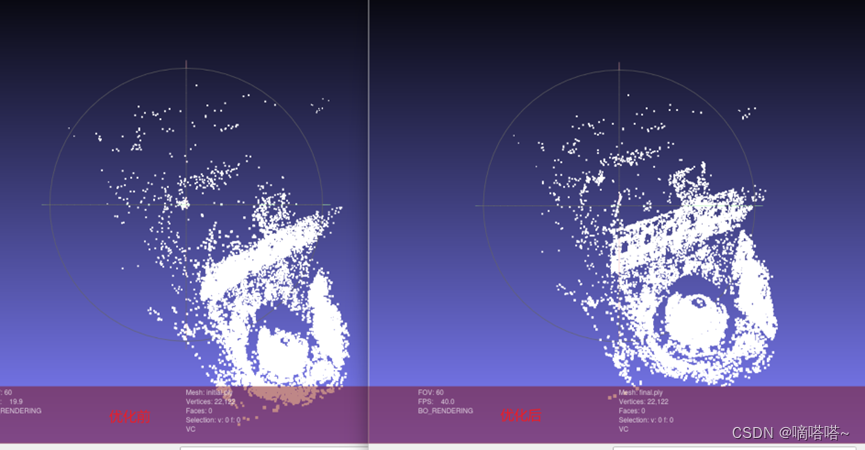
在这里插入图片描述

1.2.4、问题记录

使用旋转向量进行坐标变换问题
下面2个函数我没法理解这两个函数有什么作用，为什么需要这两个函数。c = -R’t这个是什么公式？

void BALProblem::CameraToAngelAxisAndCenter(const double *camera,
double *angle_axis, double *center) const {
   
   
	VectorRef angle_axis_ref(angle_axis, 3);
	if (use_quaternions_) {
   
   
		QuaternionToAngleAxis(camera, angle_axis);
	} else {
   
   
		/* ConstVectorRef 保证参数不会被改变 */
		angle_axis_ref = ConstVectorRef(camera, 3