三角形面积并-扫描线，计算几何

P4406 三角形面积并-扫描线，计算几何

题目描述

题解

首先，我们将整个图形的各个交点求出来，然后按照横坐标升序排列，我们就可以发现两个点所在平行于y轴的直线之间的面积是梯形，然后扫描线扫一遍就好了。
注意
1，精度问题
2，对于特殊情况如下图，要特判

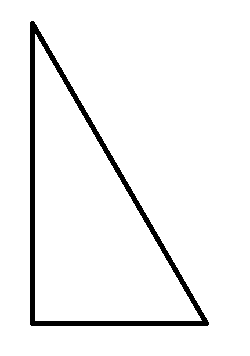
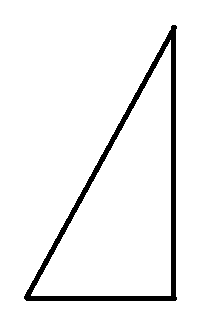
代码

#include<bits/stdc++.h>
#define M 109
using namespace std;
int n,cnt,tot;
double now,ans,last,p[M<<10];
const int inf=1e9;
const double eps=1e-12;
struct point{
	double x,y;
	point(double a=0,double b=0){x=a,y=b;}
	friend inline point operator+(const point &a,const point &b){return point(a.x+b.x,a.y+b.y);}
	friend inline point operator-(const point &a,const point &b){return point(a.x-b.x,a.y-b.y);}
	friend inline double operator*(const point &a,const point &b){return a.x*b.y-b.x*a.y;}
	friend inline double operator^(const point &a,const point &b){return a.x*b.x+a.y*b.y;}
	inline double dist(){return sqrt(x*x+y*y);}
}a[M],q[M];
struct line{
	point a,b;
}l[M][4];
bool check(double x,line a){
	if(x+eps>a.a.x&&x<eps+a.b.x) return true;
	else return false;
}
bool cmp(const point &a,const point &b){
	if(a.x!=b.x) return a.x<b.x;
	return a.y<b.y;
}
point inter(line a,line b){
	double k1,k2,t;
	k1=(b.b-a.a)*(a.b-a.a);
	k2=(a.b-a.a)*(b.a-a.a);
	t=k1/(k1+k2);
	return point(b.b.x+(b.a.x-b.b.x)*t,b.b.y+(b.a.y-b.b.y)*t);
}
double getans(double x,int type){
	tot=0;line w;
	w.a=point(x,-inf),w.b=point(x,inf);
    for(int i=1;i<=n;i++){
        if(l[i][type].b.x-l[i][type].a.x<eps&&x-l[i][type].a.x<eps) continue;
        double minx=inf,maxn=-inf;
        for(int j=1;j<=3;j++){
            if (x<l[i][j].a.x||x>l[i][j].b.x) continue;
            if (l[i][j].b.x-l[i][j].a.x<eps) continue;
            point t=inter(l[i][j],w);
            minx=min(minx,t.y),maxn=max(maxn,t.y);
        }if(maxn-minx>eps) q[++tot]=point(minx,maxn);
    }sort(q+1,q+tot+1,cmp);
    if(!tot) return 0;
    double L=q[1].x,R=q[1].y,sum=0;
    for(int i=2;i<=tot;i++){
        if(q[i].x-R>eps) sum+=R-L,L=q[i].x,R=q[i].y;
        else R=max(R,q[i].y);
    }sum+=R-L;
    return sum;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=3;j++) scanf("%lf%lf",&a[j].x,&a[j].y);
		sort(a+1,a+4,cmp);a[4]=a[1];
		for(int j=1;j<=3;j++){
			p[++cnt]=a[j].x;
			if(a[j].x>a[j+1].x+eps) swap(a[j],a[j+1]);
			l[i][j].a=a[j],l[i][j].b=a[j+1];
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=3;j++)
			for(int k=i+1;k<=n;k++)
				for(int e=1;e<=3;e++){
					point t=inter(l[i][j],l[k][e]);
					//printf("%.2lf\n",t.x);
					if(check(t.x,l[i][j])&&check(t.x,l[k][e])) p[++cnt]=t.x;
				}//for(int i=1;i<=cnt;i++) printf("%.2lf ",p[i]);
	sort(p+1,p+cnt+1);
	cnt=unique(p+1,p+cnt+1)-p-1;
	for(int i=1;i<=cnt;i++){
		now=getans(p[i],1);
		if(i>1) ans+=(now+last)*0.5*(p[i]-p[i-1]);
		last=getans(p[i],2);
		//printf("%.2lf %.2lf\n",last,now);
	}printf("%.2lf\n",ans-(1e-5));
	return 0;
}