LeetCode刷题|897递增顺序搜索树

最新推荐文章于 2024-03-05 19:30:45 发布

原创最新推荐文章于 2024-03-05 19:30:45 发布 · 157 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#指针 #链表 #leetcode #算法 #数据结构

算法与数据结构专栏收录该内容

22 篇文章

订阅专栏

本文介绍了解决“递增顺序搜索树”问题的两种方法。解法一通过中序遍历将节点值存储到数组中，再重新构建新树；解法二则在遍历过程中直接调整节点指针指向。

终于结束了几天的动态规划，迎来了今天这一道简单题。但是仔细一看，这一道跟树相关的简单题好像也没有那么简单，至少对于我来说是这样的。刷了这么久的题，对树的题目做的还是比较少的，正好乘今天好好学一下。

题目描述

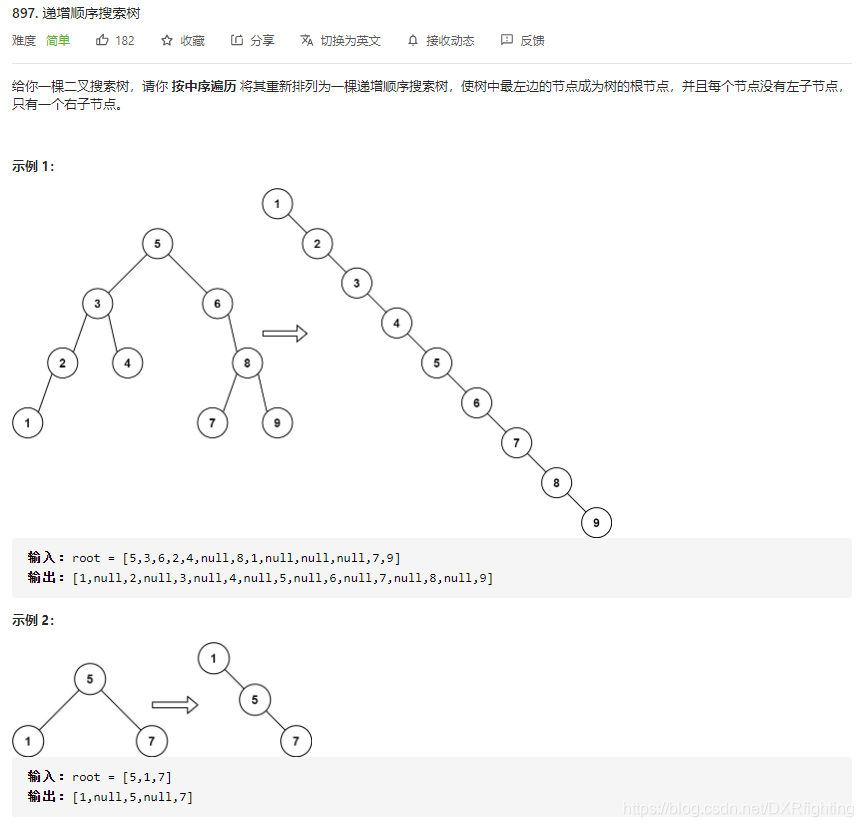
在这里插入图片描述
题目地址：递增顺序搜索树

解法一

解法一的思想比较简单直接，就是直接中序遍历然后把所有元素存储到一个数组中，然后在从数组中拿出元素重新构建一颗树。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def increasingBST(self, root: TreeNode) -> TreeNode:
        def dfs(root: TreeNode, ans: List) -> List:
            if root == None:return 
            dfs(root.left, ans)
            ans.append(root.val)  
            dfs(root.right, ans)
        nums = []
        dfs(root, nums)
        dummynode = TreeNode(-1)
        currentnode = dummynode
        for i in nums:
            currentnode.left = None
            currentnode.right = TreeNode(i)
            currentnode = currentnode.right
        return dummynode.right

这里又用到了哑结点，哑结点在很多跟链表和树有关的题目中都十分有用，可以省去一些复杂的边界判断。

解法二

解法二也是我最开始想到的方法，那就是在中序遍历的过程中直接改变指针的指向。但是我自己没有做出来，看了答案才明白怎么做。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def increasingBST(self, root: TreeNode) -> TreeNode:
        dummynode = TreeNode(-1)
        self.currentnode = dummynode
        self.dfs(root)
        return dummynode.right

    def dfs(self, node: TreeNode) -> List:
        if node == None:return 
        self.dfs(node.left)
        self.currentnode.right = node
        node.left = None
        self.currentnode = node
        self.dfs(node.right)