LeetCode刷题|503下一个更大元素 二

还是今天的每日一题，今天的是一个中等难度的题目。先看一下题目描述吧。

题目描述

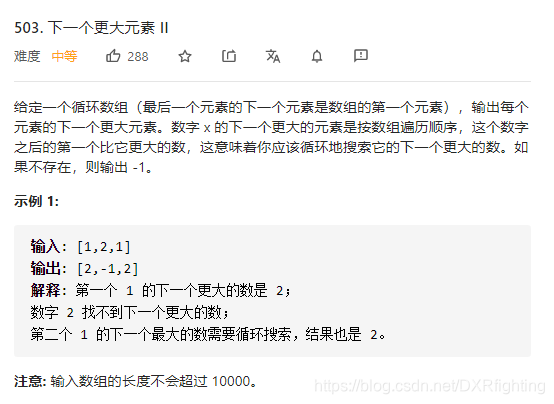
简单解释一下就是寻找数组中每一个元素的下一个比它大的元素，这个数组是一个循环数组。

暴力解法（已失败）

看到这个题目，果然我只想得到暴力解法。所谓的暴力解法，就是遍历数组中每一个元素，然后再从当前元素开始再遍历数组，直到找到比当前元素大的下一个元素，然后开始下一轮遍历。这个方法的时间复杂度很显然的O(n**2)。

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        result = []
        for i in range(0,n):
            if nums[i] == max(nums):
                result.append(-1)
            # if i==n-1:
            #     for k in range(0,n):
            #         if nums[k]>nums[i]:
            #             result.append(nums[k])
            #             break
            for j in range(i+1,n):
                if nums[j]>nums[i]:
                    result.append(nums[j])
                    break
            if len(result)<i+1:
                for k in range(0,i):
                    if nums[k]>nums[i]:
                        result.append(nums[k])
                        break
        return result

for循环第一个判断的意思是如果为数组中最大的元素，那么是找不到下一个更大元素的，按照题目要求直接添加-1。接下来就是从当前元素开始往后遍历，如果遍历到数组最后，结果数组中都还没有添加元素，说明数组后面没有比当前元素更大的元素。那么因为这是一个循环数组，所以我们需要再从数组开始往后找。如果找到更大元素，那么就直接退出循环。开始对下一个元素循环。

然而，经过我多次修改之后，我满以为这次可以通过了。没想到测试用例直接来了一个[0,9999]的数组，我这个n的平方时间复杂度的算法毫无疑问超出时间限制了。😭
于是还是得找到效率更高的算法。

单调栈

我们先看一下前面说的暴力解法它为什么这么慢，如果我们有一个数组是[5,4,3,2,1,6]，用暴力法的话前面五个数每一个都要遍历到最后一个数才能找到比它更大的数，但是因为4,3，2,1都比5小，因此实际上5后面比5大的数是6，因为这几个数还是递减的，那么4,3，2,1就不用判断了，他们后面比他们大的数肯定也是6，这样的话我们就能节省时间了。这里就可以用一个单调栈来实现，所谓单调栈，就是栈内元素按照单调递增或递减的顺序加入。我们每次判断栈顶元素跟当前元素的大小关系，如果小于栈顶元素，那就加入栈内，如果大于栈顶元素栈内元素出栈并且在结果数组中加入当前元素。如果栈为空的话同样把当前元素加入栈内。

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        ret = [-1] * n
        stk = list()

        for i in range(n * 2 - 1):
            while stk and nums[stk[-1]] < nums[i % n]:
                ret[stk.pop()] = nums[i % n]
            stk.append(i % n)
        
        return ret

今天的每日一题学到的主要内容就是单调栈了，这个数据结构和技巧应该挺有用的，记录一下，经常复习。