task05吃瓜支持向量机

1. 简介

支持向量机是一种经典的二分类模型，基本模型定义为特征空间中最大间隔的线性分类器，其学习的优化目标便是间隔最大化，因此支持向量机本身可以转化为一个凸二次规划求解的问题。
2. 最大间隔与支持向量

函数间隔不适合用来最大化间隔，因此这里我们要找的最大间隔指的是几何间隔，于是最大间隔分类器的目标函数定义为：

一般地，我们令r^为1（这样做的目的是为了方便推导和目标函数的优化），从而上述目标函数转化为：

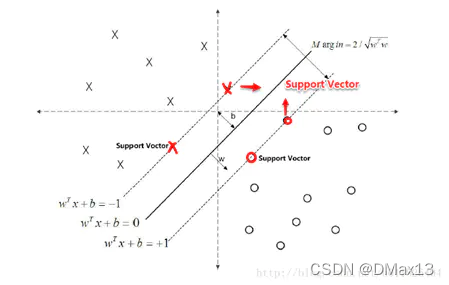
对于y(w’x+b)=1的数据点，即右图中位于w’x+b=1或w’x+b=-1上的数据点，我们称之为支持向量（support vector），易知：对于所有的支持向量，它们恰好满足y*(w’x*+b)=1，而所有不是支持向量的点，有y*(w’x*+b)>1。

3. 对偶问题
对于上述得到的目标函数，求1/||w||的最大值相当于求||w||^2的最小值，因此很容易将原来的目标函数转化为：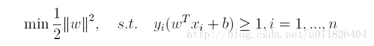
即变为了一个带