task02LDA

datawhale task02

3.1 基本形式

线性模型的本质是通过一个所有属性的线性组合进行预测的函数，即

$f(x)=w_1{x}_1+w_2{x}_2+...+w_d{x}_d+b$
一般用向量形式写成
$$f(x)=w^{T}x+b$$其中w表示属性在预测中的重要性。
机器学习三要素： (1)确定研究模型 (2)确定损失函数 (3)确定优化算法

3.2 线性回归

1. 从最简单的单属性的情形入手。若属性值之间存在“序”关系。可将其连续化转化为连续值
2. 若属性之间不存在序关系，则需将其转化为k维向量。

首先我们需要明晰：我们最终想要做到的是通过线性回归最终学得
$f(x_i)=w{x}_i+b$,使得f(xi)≈yi.而在此式中，未知量是w,b,所以线性回归得最终目标应该就是使得学习器中二者的误差最小，以使得最终的学习结果更加接近于真实值。这里我们使用均方误差来作为其性能度量，即



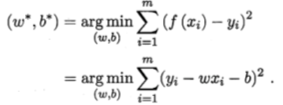
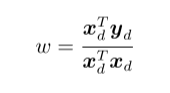
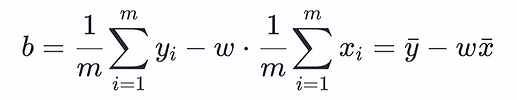
多元线性回归： 写为矩阵形式，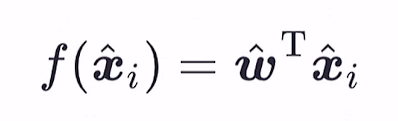

若XX.T满秩，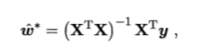
若不满秩，则有多个参数可满足最小均方误差，可引入正则化项
广义线性回归模型：g单调可微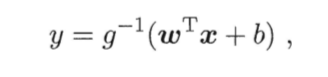

对数几率回归

信息熵：自信息的期望，度量随机变量x的不确定性。

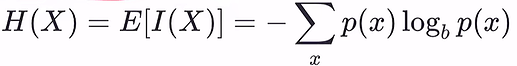
交叉熵：最小化相对熵等价于最小化交叉熵

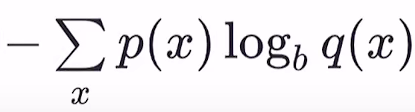
LDA: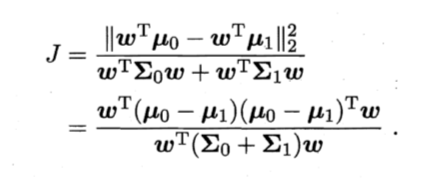

类内散度矩阵：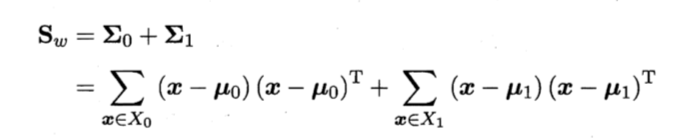

类间散度矩阵：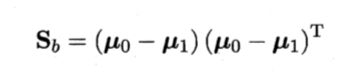

原式可写为：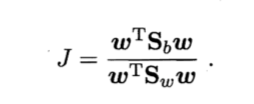

利用拉格朗日乘子法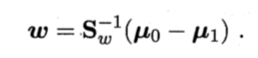

多分类情况可以看为是$W=（w_1,w_2,w_3,w_4\dots ,w_n$的求解，将一个多分类拆分为多个二分类求解