Hung-yi Li Machine Learning 2019 Task1

李宏毅机器学习 Machine_Learning_2019_Task1

机器学习打卡任务内容：

了解什么是Machine learning

学习中心极限定理，学习正态分布，学习最大似然估计

• 推导回归 Regression Loss function
• 学习损失函数与凸函数之间的关系
• 了解全局最优和局部最优

学习导数，泰勒展开

• 推导梯度下降公式
• 写出梯度下降的代码

学习L2-Norm，L1-Norm，L0-Norm

• 推导正则化公式
• 说明为什么用L1-Norm代替L0-Norm
• 学习为什么只对w/Θ做限制，不对b做限制

Task1 Implementation:

• 了解 Machine Learning 的概念；

  • What is Machine Learning?

    • A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
    • 机器学习是计算机科学的一个子领域，它关注的是建立一种算法，这种算法要想有用，就必须依赖于一些现象的实例集。这些例子可以来自nature，可以由人类手工制作，也可以由其他算法生成.
    • 一言以蔽之：通过收集数据集，并基于该数据集建立一个统计模型来解决实际问题的过程。即，这个统计模型被假定用来解决实际问题，以便获取有用的信息.
      
      

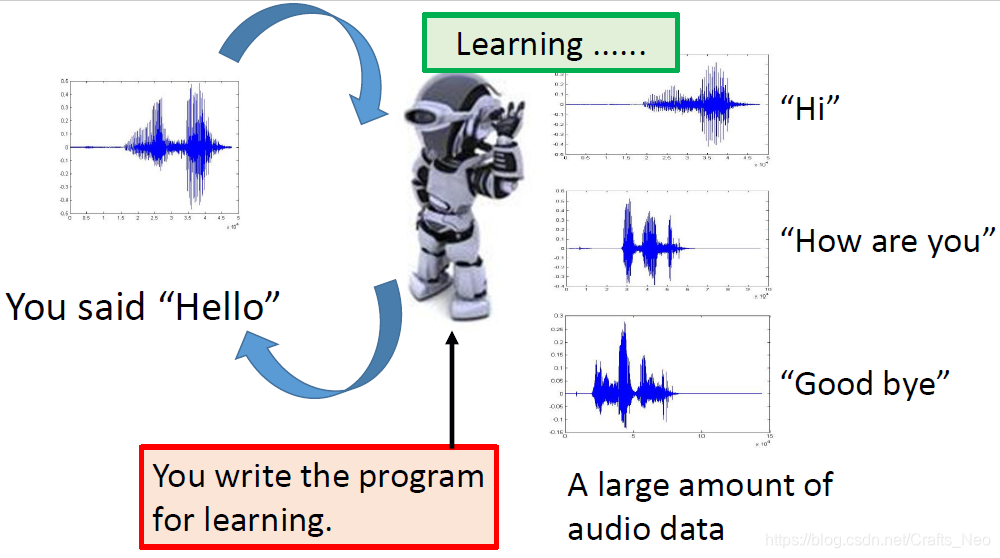
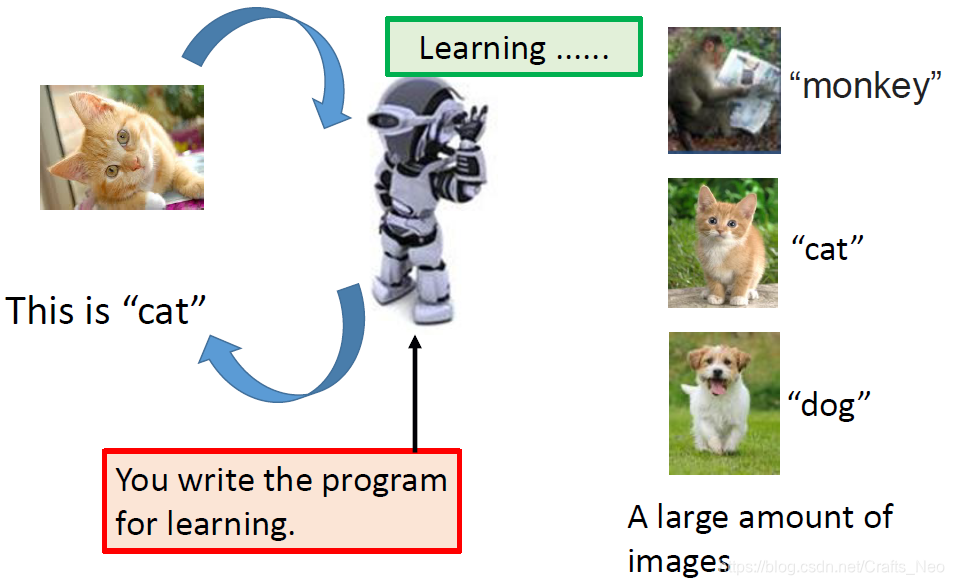
  • Why Use Machine Learning?

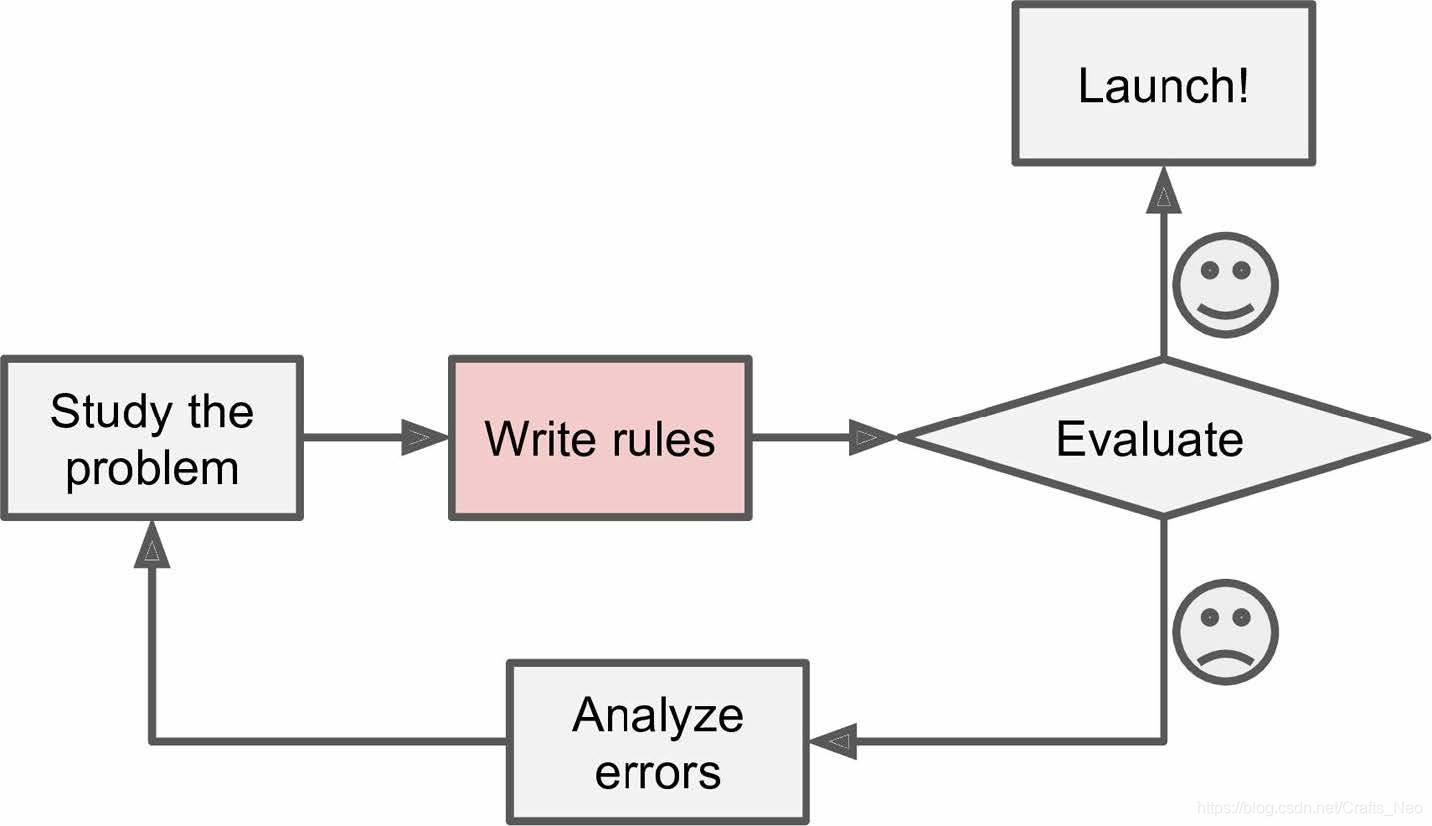
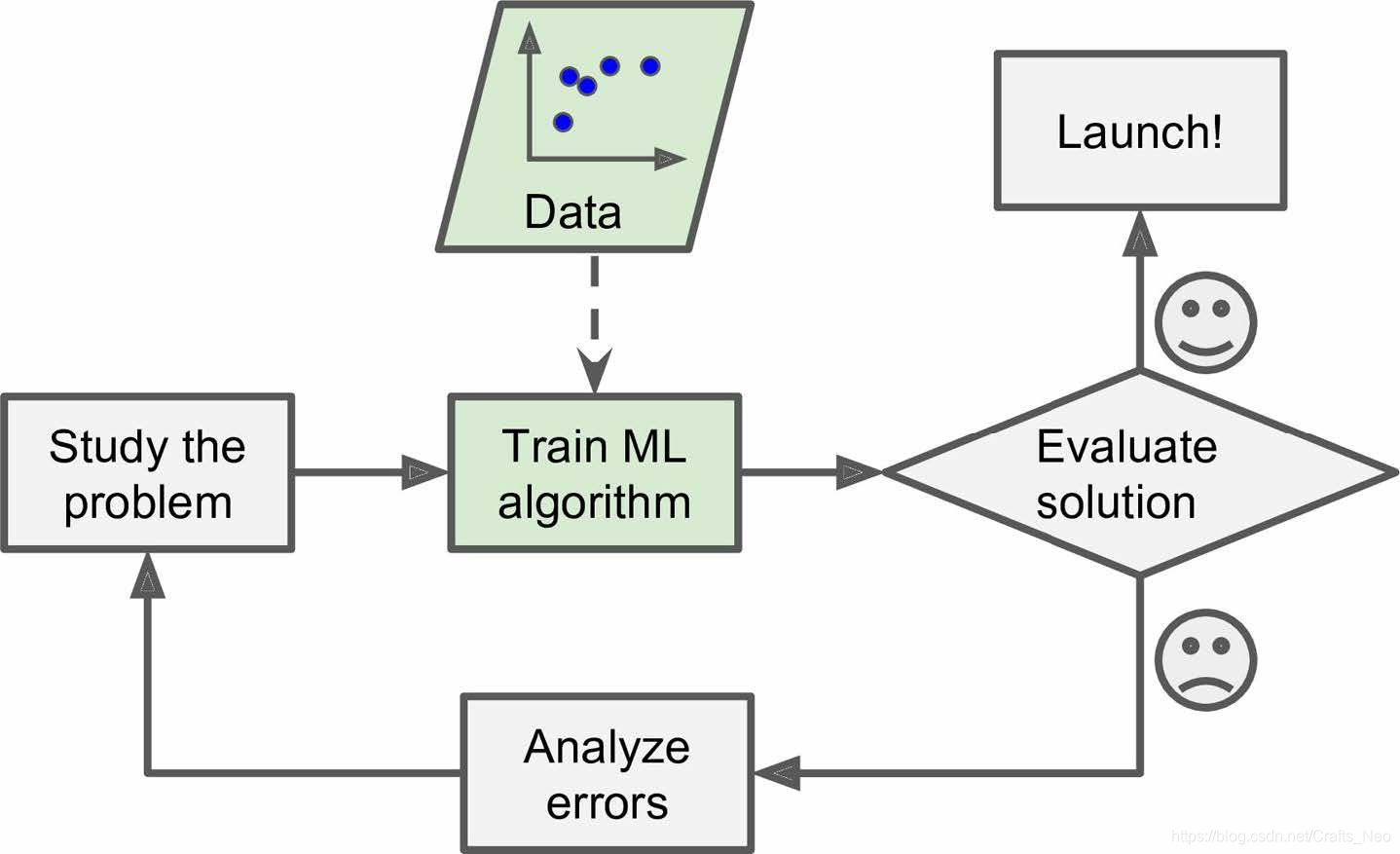
• How to Learn Machine Learning?

  

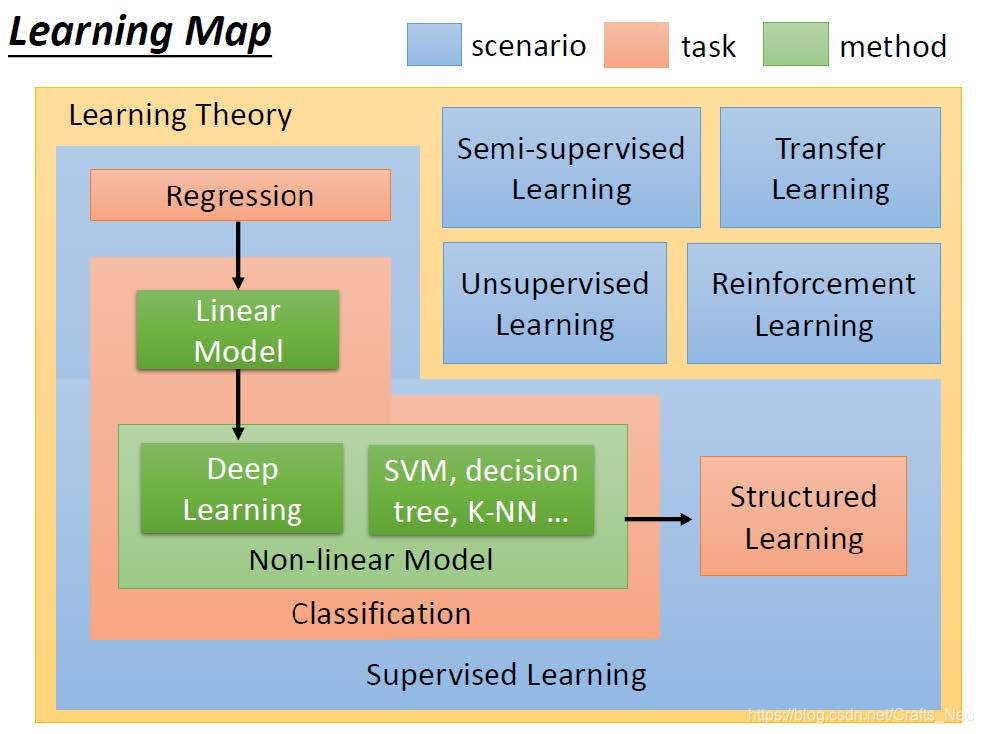
• 学习中心极限定理，学习正态分布，学习最大似然估计

• 最优化理论及方法

• 高等数学

• 统计学

• 概率论

• 参数估计

• 正态分布与中心极限定理(中心极限定理是正态分布的一个前置知识)

  • 如果误差可以看作许多微小量的叠加，则根据中心极限定理(用样本的平均值估计总体的期望)，随机误差理所当然服从正态分布；

  • 假设一随机变量X服从一个期望和方差分别为
    $$\mu 和{\sigma }^2$$
    的正态分布，概率密度函数为
    $$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$
    则可以记为
    $$X\sim N(\mu ,{\sigma }^2)$$
    图例表示
    

  • 正态分布为何如此常见？其真正原因是中心极限定理 (Central Limit theorem)，如果一个事物受到多种因素的影响，无论每个因素本身服从什么分布，这些因素加总后，结果的平均值就是正态分布；

  • 正态分布值适合于各种因素叠加的情况，如果这些因素不是彼此独立的，会相互加强影响，则就不会服从正态分布。如果各种因素对结果的影响不是相加，而是相乘，则最终结果将会是对数正态分布.

• 最大似然估计与贝叶斯推理 (新增专题 · 待完善)

  • 参数的意义

• 最大似然估计的直观解释

  • 最大似然估计的计算

• MLE

  • 对数似然估计

• 最大似然估计是否总能得到精确解？

  • 为何称作“ 『最大似然』or 『最大可能』”，而不是『最大概率』?

• 最小二乘参数估计和最大似然估计的结果相同的条件是什么？

  • 贝叶斯定理
    • 定义
    • 举例
  • 为何贝叶斯定理能结合先验概率？
  • 贝叶斯推理

• 定义

  • 使用贝叶斯定理处理数据分布

  • 贝叶斯定理的模型形式

  • 贝叶斯推断示例

  • 何时 最大后验概率 (Maximum A Posteriori) MAP 估计 与 最大似然 (Maxmium Likelihood Estimation MLE) 估计相等？

  • 推导回归Regression Loss function；

    • 分类的目标变量是标称型数据，而回归则是对连续型的数据做出处理，回归的目的是预测数值型数据的目标值；

    • 典型回归问题：线性回归之 Least Mean Squares (LMS) 最小二乘法(回归问题)，以及逻辑回归的LR模型(分类问题)

      • 损失函数 loss function：

        • 定义1：

        $$:\sum _{i=1}^m{\left(y_i-x_i^{T}w\right)}^2$$

        其中，输入数据xi，回归系数w，预测结果yi

        • 定义2：
          $$J(\mathbf{w})=\frac{1}{2}\sum _{i=1}^m{\left(h_{\mathbf{w}}\left({\mathbf{x}}_i\right)-y_i\right)}^2$$
          主要目的是让 hw 尽量接近 yi，选择 w 来最小化 J(w)

          函数f定义形式如下：
          $$f\left(u_1,u_2,\dots ,u_n\right):{\mathbb{R}}^n\mapsto \mathbb{R}$$
          对 ui 进行偏导操作：
          $$\frac{\partial }{\partial u_i}f\left(u_1,u_2,\dots ,u_n\right):{\mathbb{R}}^n\mapsto \mathbb{R}$$
          对应梯度：
          $$\nabla f=⟨\frac{\partial }{\partial u_1}f,\frac{\partial }{\partial u_2}f,\dots ,\frac{\partial }{\partial u_n}f⟩$$
          对wj求偏导的计算过程：
          $$\begin{array}{rl}\frac{\partial }{\partial w_j}J(\mathbf{w})& =\frac{\partial }{\partial w_j}\frac{1}{2}\sum _{i=1}^m{\left(h_{\mathbf{w}}\left({\mathbf{x}}_i\right)-y_i\right)}^2\\ & =\frac{1}{2}\cdot 2\sum _{i=1}^m\left(h_{\mathbf{w}}\left({\mathbf{x}}_i\right)-y_i\right)\frac{\partial }{\partial w_j}\left(h_{\mathbf{w}}\left({\mathbf{x}}_i\right)-y_i\right)\\ & =\sum _{i=1}^m\left(h_{\mathbf{w}}\left({\mathbf{x}}_i\right)-y_i\right)\frac{\partial }{\partial w_j}\left(\sum _{l=0}^n{w}_l{x}_{i,l}-y_i\right)\\ & =\sum _{i=1}^m\left(h_{\mathbf{w}}\left({\mathbf{x}}_i\right)-y_i\right)x_{i,j}\end{array}$$
          将偏导设为0，我们将得到一个线性方程组：
          $$求关于w的梯度：\begin{array}{rl}{\nabla }_{\mathbf{w}}J& ={\nabla }_{\mathbf{w}}(\mathbf{X}\mathbf{w}-\mathbf{y}{)}^T(\mathbf{X}\mathbf{w}-\mathbf{y})\\ & ={\nabla }_{\mathbf{w}}\left({\mathbf{w}}^T{\mathbf{X}}^T\mathbf{X}\mathbf{w}-{\mathbf{y}}^T\mathbf{X}\mathbf{w}-{\mathbf{w}}^T{\mathbf{X}}^T\mathbf{y}+{\mathbf{y}}^T\mathbf{y}\right)\\ & =2{\mathbf{X}}^T\mathbf{X}\mathbf{w}-2{\mathbf{X}}^T\mathbf{y}\end{array}$$

          $$将偏导设为0，求出w：\begin{array}{rl}2{\mathbf{X}}^T\mathbf{X}\mathbf{w}-2{\mathbf{X}}^T\mathbf{y}& =0\\ \Rightarrow {\mathbf{X}}^T\mathbf{X}\mathbf{w}& ={\mathbf{X}}^T\mathbf{y}\\ \Rightarrow \mathbf{w}={\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}^T\mathbf{y}& \end{array}$$

      • LR模型(构造似然函数)：

        

  • 学习损失函数与凸函数之间的关系；

    • 损失函数：在监督学习中，损失函数刻画了模型和训练样本的匹配程度，即定义了模型的评估指标.
    • 凸函数的几何解释是：函数图像上的任意两点确定的弦在图像的上方；
    • 凸集C上的任意有限个凸函数的任意非负组合仍是凸函数；
    • 根据最优化理论，任何最大化问题统一转化为最小问题，任何凹函数统一转化为凸函数，因此将最大化似然函数取反转化为最小优化函数，并将其取反的函数称之为损失函数.

  • 了解全局最优和局部最优.

    • 模型的最优解

      • 局部最优解
        f ( x ∗ ) ≤ f ( x ) , ∀ x ∈ D ∩ U δ ( x ∗ ) , 其 中 ， U δ ( x ∗ ) = { x ∈ R n ∣ ∥ x − x ∗ ∥ &lt; δ } . f\left(x^{*}\right) \leq f(x), \forall x \in D \cap U_{\delta}\left(x^{*}\right),\\ 其中，U_{\delta}\left(x^{*}\right)=\left\{x \in R^{n} |\|x-x *\|&lt;\delta\right\}. f(x∗)≤f(x),∀x∈D∩Uδ​(x∗),其中，Uδ​(x∗)={x∈Rn∣∥x−x∗∥<δ}.

      • 全局最优解
        $$f\left(x^{\ast }\right)\le f(x),\forall x\in D.$$

      • 全局最优解是局部最优解

        

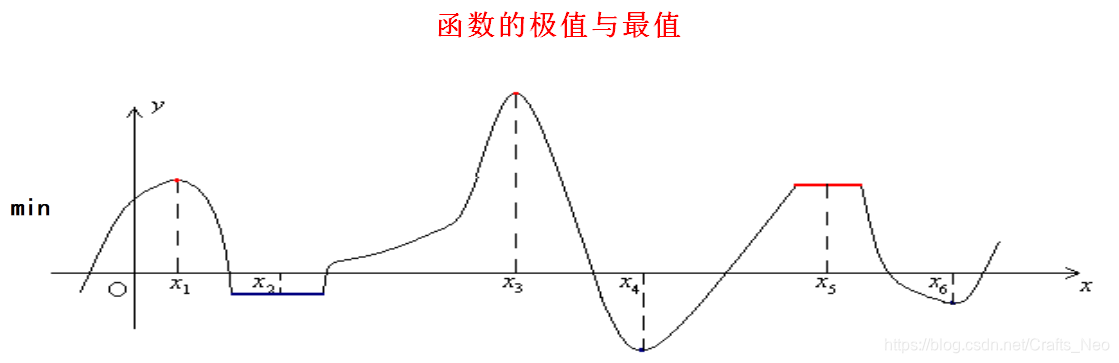
• 学习导数，Taylor 展开式

  • 导数与梯度的关系

    • 梯度是一个向量，也可以理解为最速上升的方向，即 每个元素 为 函数 对 一元变量的 偏导数.

    • $$\nabla f(x)={\left(\frac{\partial f(x)}{\partial x_1},\cdots ,\frac{\partial f(x)}{\partial x_n}\right)}^{\mathrm{T}}$$

  • 多元函数的Taylor展开

    • 一阶Taylor 展开（一阶中值定理）
      $$f(x)=f(y)+\nabla f(y{)}^T(x-y)+o(\Vert x-y\Vert )$$

    • 二阶Taylor 展开（二阶中值定理）

      $$f(x)=f(y)+\nabla f(y{)}^T(x-y)+\frac{1}{2}(x-y{)}^T{\nabla }^{2}f(y)(x-y)+o\left(\Vert x-y{\Vert }^2\right)$$

  • 最速下降法与Newton法
    

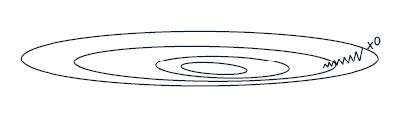
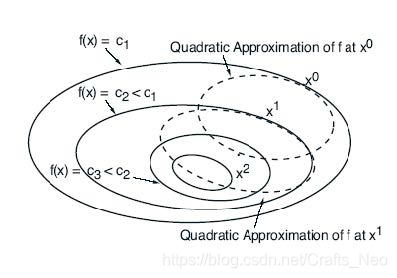    • $$最速下降法：x^{k+1}=x^k-{\alpha }^k\nabla f\left(x^k\right)$$
      $$Newton牛顿法：x^{k+1}=x^k-{\alpha }^k{\left({\nabla }^{2}f\left(x^k\right)\right)}^{-1}\nabla f\left(x^k\right)$$

  • 推导梯度下降(Gradient Descent)公式；

    • J在点w处的梯度可以看作是一个矢量，表示哪条路是上坡的；

    • 如果这是一个误差 or 损失函数，我们想把它往下移，即取梯度的负方向.

      

      

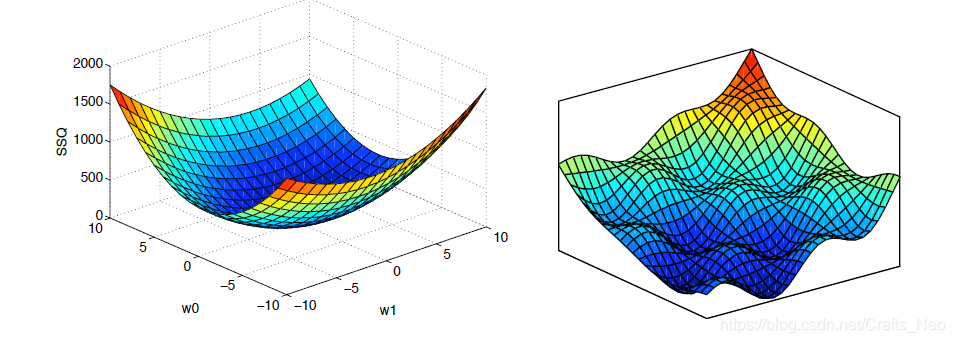
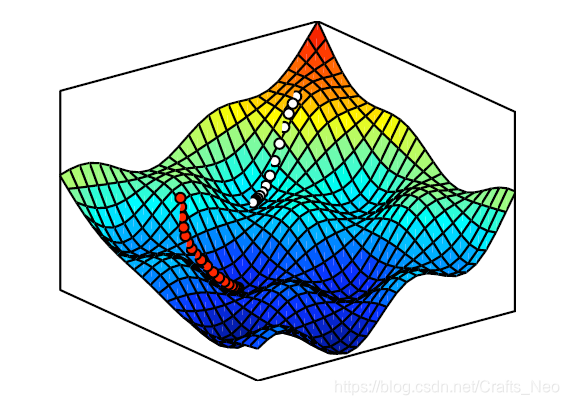
      • 算法推导(Gradient Descent Algorithm)

        • 假设梯度容易计算得到
          $$\nabla J$$

        • 我们想产生一个向量序列
          $${\mathbf{w}}^1,{\mathbf{w}}^2,{\mathbf{w}}^3,\dots$$
          最终目标是：
          $$\begin{array}{l}J\left({\mathbf{w}}^1\right)>J\left({\mathbf{w}}^2\right)>J\left({\mathbf{w}}^3\right)>\dots \\ {\lim }_{i\to \infty }{\mathbf{w}}^i=\mathbf{w}\text{ 且 }\mathbf{w}\text{ 是局部最优. }\end{array}$$

        • 算法：
          $$Given：{\mathbf{w}}^0,\text{ do for }i=0,1,2,\dots$$

          $${\mathbf{w}}^{i+1}={\mathbf{w}}^i-{\alpha }_i\nabla J\left({\mathbf{w}}^i\right).$$

          其中，
          $${\alpha }_i$$
          要求大于0，为第i次迭代对应的步长 or 学习率，

  • 写出梯度下降代码(基于Armijo非精确线搜索的最速下降法求解无约束优化问题).

    • % 定义一个函数:f=100(x(1)^2-x(2))^2+(x(1)-1)^2
      function f=fun(x)
      f=100*(x(1)^2-x(2))^2+(x(1)-1)^2;
      

    • % 计算目标函数对应的梯度
      function g=gfun(x)
      g=[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1), -200*(x(1)^2-x(2))]';
      

    • function [x,val,k] = grad(fun,gfun,x0)
      
      % 功能: 用基于Armijo非精确线搜索的最速下降法求解无约束优化问题 min f(x)
      % 输入: x0是初始点, fun, gfun分别是目标函数和梯度
      % 输出: x, val分别是近似最优点和最优值, k是迭代次数
      
      kmax = 5000; %最大迭代次数
      rho = 0.5; sigma = 0.4;
      k = 0; epsilon = 1e-5;
      while(k<kmax)
          g = feval(gfun, x0); %计算梯度
          d = -g; %计算搜索方向
          if(norm(d)<epsilon)
              break;
          end
          m=0;
          mk=0;
          while(m<20) %Armijo搜索
              if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d)
                  mk=m;
                  break;
              end
              m=m+1;
          end
          x0 = x0+rho^mk*d;
          k = k+1;
      end
      x = x0;
      val = feval(fun,x0);
      

    • %基于Armijo非精确线搜索的最速下降法求解无约束优化问题
      x0 = [-1.2 1]';%初始点
      [x,val,k] = grad('fun','gfun',x0)
      

• 学习 L2-Norm，L1-Norm，L0-Norm

  • 推导正则化(regularization)公式；

    • 正则化是一个通用的算法和思想，所有会产生过拟合现象的算法都可以使用正则化来避免过拟合

  • 说明为什么用 L1-Norm 代替 L0-Norm；

    • 向量范数
      $$\begin{gathered} \Vert x{\Vert }_1=\sum _{i=1}^n\left|x_i\right|. \\ 向量的l1-norm \end{gathered}$$

      $$\begin{gathered} \Vert x{\Vert }_2={\left(\sum _{i=1}^n{\left|x_i\right|}^2\right)}^{\frac{1}{2}}. \\ 向量的l2-norm \end{gathered}$$

    • L1-norm 相当于L0-norm，使得特征较多为0，即特征稀疏化，而L0-norm难于优化，因此常用L1-norm代替L0-norm，方便特征提取.

    • 线性模型的L2-Regularization正则化:

      • 对权重进行平方惩罚:
        $$L2正则化or权重衰减：\frac{1}{2}{\left({\Phi }_{\mathrm{W}}-\mathrm{y}\right)}^T\left({\Phi }_{\mathrm{W}}-\mathrm{y}\right)+\frac{\lambda }{2}{\mathrm{w}}^T\mathrm{w}$$
        重新组合:
        $$J_D(\mathbf{w})=\frac{1}{2}\left({\mathbf{w}}^T\left({\mathbf{\Phi }}^T\mathbf{\Phi }+\lambda \mathbf{I}\right)\mathbf{w}-{\mathbf{w}}^T{\mathbf{\Phi }}^T\mathbf{y}-{\mathbf{y}}^T\mathbf{\Phi }\mathbf{w}+{\mathbf{y}}^T\mathbf{y}\right)$$
        令JD(W)的梯度关于w的偏导设为0：
        $$\mathbf{w}={\left({\mathbf{\Phi }}^T\mathbf{\Phi }+\lambda I\right)}^{-1}{\mathbf{\Phi }}^T\mathbf{y}$$
        整理得：
        $$\arg \underset{\mathbf{w}}{\min }\frac{1}{2}(\mathbf{\Phi }\mathbf{w}-\mathbf{y}{)}^T(\mathbf{\Phi }\mathbf{w}-\mathbf{y})+\frac{\lambda }{2}{\mathbf{w}}^T\mathbf{w}={\left({\mathbf{\Phi }}^T\mathbf{\Phi }+\lambda I\right)}^{-1}{\mathbf{\Phi }}^T\mathbf{y}$$

        1. 如果lambda为0，则为最小二乘线性回归；

        2. 如果lambda接近无穷大，则w设为0；

        3. 正lambda可能会致w的值小于一般的线性解.

           在保持权值范数有界的情况下最小化误差:
           $$\begin{array}{rl}\underset{\mathbf{w}}{\min }{J}_D(\mathbf{w})& =\underset{\mathbf{w}}{\min }(\mathbf{\Phi }\mathbf{w}-\mathbf{y}{)}^T(\mathbf{\Phi }\mathbf{w}-\mathbf{y})\\ \text{ such that }{\mathbf{w}}^T\mathbf{w}& \le \eta \end{array}$$
           构造拉格朗日函数：
           $$L(\mathbf{w},\lambda )=J_D(\mathbf{w})-\lambda \left(\eta -{\mathbf{w}}^T\mathbf{w}\right)=(\mathbf{\Phi }\mathbf{w}-\mathbf{y}{)}^T(\mathbf{\Phi }\mathbf{w}-\mathbf{y})+\lambda {\mathbf{w}}^T\mathbf{w}-\lambda \eta$$
           固定lambda，其中
           $$\eta ={\lambda }^{-1}$$
           w的求解同上

      

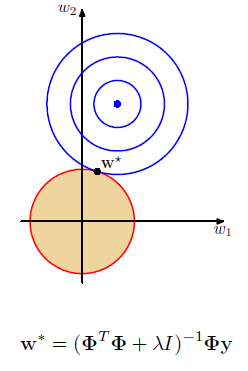
      1. 如果lambda的值较好，则L2正则化可以很好地避免过拟合；
      2. lambda的选择一般较为困难，常采用的方法是交叉验证；
      3. 如果输入中有不相关的特性，L2将会给其一个小的，但非零的权重；
      4. 一般理想情况下，不相关的输入的权值应该恰好等于0.

      • 线性模型的L1-Regularization正则化

        • 不再是权值向量的L2范数有界，而是要求L1范数有界，即Lasso Regression:
          $$\begin{array}{rl}\underset{\mathbf{w}}{\min }{J}_D(\mathbf{w})& =\underset{\mathbf{w}}{\min }(\mathbf{\Phi }\mathbf{w}-\mathbf{y}{)}^T(\mathbf{\Phi }\mathbf{w}-\mathbf{y})\\ \text{ such that }& \sum _{i=1}^n\left|w_i\right|\le \eta \end{array}$$
          优化问题转化为QP(二次规划)问题，权重的每个可能符号都有一个约束条件(n个权值，有2^n个限制条件)：
          当有两个权值时
          $$\begin{array}{rl}\underset{w_1,w_2}{\min }& \sum _{j=1}^m{\left(y_j-w_1{x}_1-w_2{x}_2\right)}^2\\ \text{ such that }{w}_1+w_2& \le \eta \\ w_1-w_2& \le \eta \\ -w_1+w_2& \le \eta \\ -w_1-w_2& \le \eta \end{array}$$
          用少量的输入就可以直接求解以上问题.

      

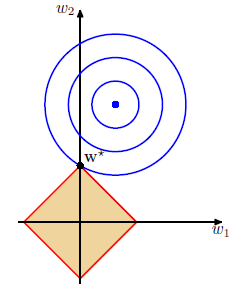
      1. 如果lambda足够大，则这个圆极有可能在一个角上与菱形相交；
      2. 使得L1正则化更有可能使某些权重恰好为0；
      3. 如果有不相关的输入特性，Lasso很可能使它们的权重为0，而L2则可能使所有的权重都变小；
      4. Lasso通常倾向于提供稀疏的解决方案；
      5. Lasso优化在计算上比L2更昂贵；
      6. 有效的解决方案就是利用大量的输入数据；
      7. 各种类型的方法中，L1-Regularization方法都非常流行.

    • L1与L2的效果对比

      

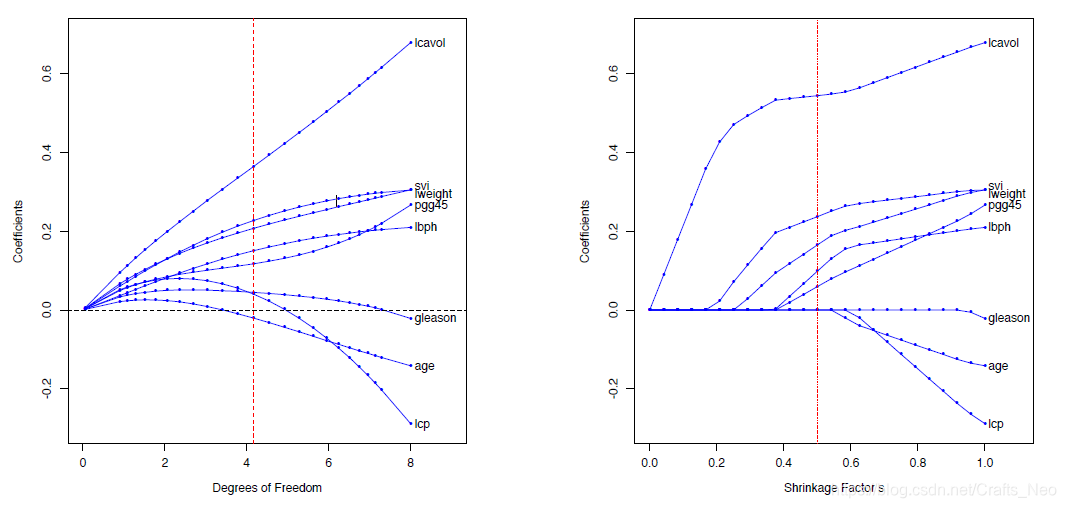
      1. 由L1引起的各组分的稀疏化；
      2. Lasso是一种有效的L1优化方法.

Summary

• 本文主要是对机器学习的基本概念进行了简单性的概述以及对回归损失函数、梯度下降法、线性模型的正则化等常用的公式进行了推导和解析，无论是对机器学习初学者 or 进阶者，希望对大家有一定的帮助和借鉴意义。本推文作为抛砖引玉之篇，鼓励大家多多讨论，多多交流，也希望大家都能耐得住寂寞，在Machine Learning的学习旅途中，收获更多，成长更多！！！

参考资源

• Hands-on Machine Learning with Scikit-learn, Keras & TensorFlow.
• Hung-yi-Lee__ML2019课程主页(包含学习资料)
• The Hundred-page Machine Learning Book.
• Hung-yi-Lee__ML2019课程主页(包含学习资料)
• AiLearning 第8章 预测数值型数据：回归.
• Hung-yi-Lee__ML2019课程视频(Bilibili)
• Hung-yi-Lee__ML2019YouTube
• Introduction to Machine Learning.
• Applied Logistic Regression.
• 百面机器学习(宝葫芦).