Option Symbol Matters: Investigating and Mitigating Multiple-Choice Option Symbol Bias of Large Language Model -25ACL
| 偏差类型 | 选项符号偏差(Option Symbol Bias) A/B/C/D) i-iv)1-4)x₁–x₄) |
|---|---|
| 致偏原因 | 关键注意力头过度关注选项符号本身,而非其语义内容;与“下一词预测”预训练范式有关 |
| 去偏方法 | CEDE:基于因果效应的激活干预方法,无需训练,推理时干预关键头的激活 |
| 使用的 LLMs | LLaMA2-7B/13B/70B, LLaMA3-8B, Mistral-7B |
步骤1:识别关键注意力头(Identifying Key Components)
目标:找出对“选项符号偏差”影响最大的注意力头。
方法:使用路径修补(Path Patching),一种因果干预方法。
- 输入:
- 参考数据 Dr:使用一组选项符号(如 A/B/C/D)的 MCQ 数据
- 干扰数据 Dc:与 Dr 内容相同,但选项符号不同(如 i/ii/iii/iv)
- 过程:
- 在 Dr上运行模型,缓存每个注意力头的激活值。(通过注意力权重对 V(值)向量进行加权求和后得到的结果。它的维度是
(batch_size, sequence_length, d_head),其中d_head是每个头的隐藏维度。d_head = d_model / num_heads = 4096 / 32 = 128) - 将某个注意力头的激活替换为 Dc中的对应激活,其余保持不变。
- 计算修补后对正确答案 logit 的影响(因果效应)。
- 在 Dr上运行模型,缓存每个注意力头的激活值。(通过注意力权重对 V(值)向量进行加权求和后得到的结果。它的维度是
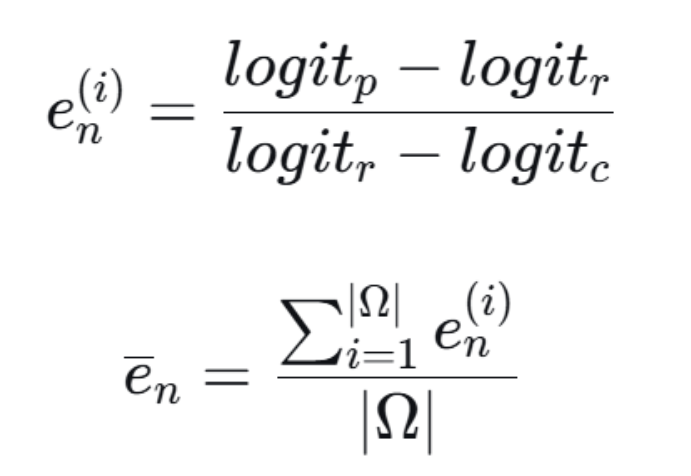
-
logit_r:模型在参考数据(如符号A/B/C/D)上,对正确答案对应符号(如B)的输出logit(未归一化的分数)。 -
logit_c:模型在干扰数据(如符号i/ii/iii/iv)上,对同一正确答案(现在对应符号ii)的输出logit。由于符号变了,模型表现通常会变差,所以logit_c通常比logit_r小。 -
logit_p:将模型在参考数据上前向传播时,某个特定注意力头的激活值,替换成它在干扰数据上计算出的激活值,然后继续完成前向传播,得到的新logit。 -
比值
e_n:如果修补某个头导致logit大幅下降(即logit_p很小),说明这个头对符号变化非常敏感,它的e_n会是一个较大的负值。这个负值越大,说明该头对“符号偏差”的“责任”越大。 -
ē_n:在所有数据对Ω上平均,得到该头的平均因果效应。 -
输出:
- 每个注意力头的因果效应值 en。
- 识别出因果效应显著(如 < -0.04)的“关键头”。
关键发现:只有少数位于中间层(如15-25层)的注意力头对符号偏差影响显著。
步骤2:解释关键头的注意力模式(Interpreting Patterns)
目标:理解这些关键头在做什么。
方法:可视化关键注意力头的注意力分布图 Aij∈Rs×s。
- 输入:MCQ 问题及其选项(使用多种符号集)。
- 过程:
- 提取关键头在生成答案时的注意力权重。
- 观察它们关注的是“选项内容”还是“选项符号”。
- 输出:
- 关键头:主要关注“选项符号”,几乎忽略选项内容。
- 非关键头:注意力更均匀分布在问题和选项内容上。
结论:关键头过度依赖符号本身,导致模型对符号变化敏感。
步骤3:干预激活以去偏(Mitigating Bias with CEDE)
目标:通过干预关键头的激活,减轻符号偏差。
方法:提出 CEDE 方法,无需训练,直接在前向传播中干预。
-
输入:
- 关键头的激活向量 vij
- 平均偏差向量 Vij(在不同符号集上平均得到)
- 每个头的因果效应 eij
-
过程:
-
计算刺激方向:
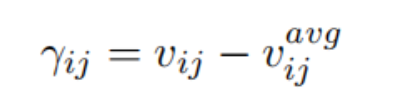
-
根据因果效应调整干预强度:
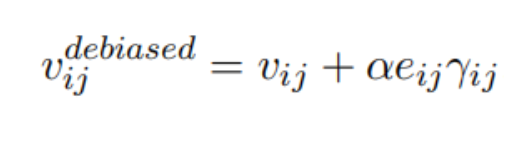
其中 e^ij 是归一化后的因果效应 -
-
输出:去偏后的激活值,用于后续预测
举例说明去偏计算过程
假设场景:
- 我们正在处理一个MCQ问题
- 我们已识别出一个关键头
18.31,其因果效应ē = -0.08(一个显著的负值)。 - 该头的激活值
v是一个向量,假设为[0.5, 1.2, -0.3, ...](4096维)。 - 我们已预先在1000个不同符号集的问题上计算了这个头的平均激活
v_avg,假设为[0.1, 0.8, -0.1, ...]。这个v_avg代表了该头对符号的“平均偏见”。 - 超参数
α设为 20。
去偏计算步骤:
- 计算刺激方向
γ:
γ = v - v_avg
假设v = [0.5, 1.2, -0.3],v_avg = [0.1, 0.8, -0.1]
那么γ = [0.5-0.1, 1.2-0.8, -0.3-(-0.1)] = [0.4, 0.4, -0.2]
这个方向指向了“当前激活”偏离“平均偏见”的方向,可能蕴含了更多与当前具体问题相关的真实答案信息。 - 计算归一化因果效应
ê:- 假设我们只干预Top-2个头,它们的原始因果效应为
[-0.08, -0.06]。 - 计算Softmax:先取指数
[e^{-0.08}, e^{-0.06}] ≈ [0.923, 0.942]。 - 求和:
0.923 + 0.942 = 1.865。 - 归一化:
ê = [0.923/1.865, 0.942/1.865] ≈ [0.495, 0.505]。 - 再乘以头数
|κ|=2:ê = [0.495*2, 0.505*2] = [0.99, 1.01]。
这样处理确保了干预强度与因果效应成正比,且覆盖更均匀。*
- 假设我们只干预Top-2个头,它们的原始因果效应为
- 计算去偏后的激活
v_debiased:
v_debiased = v + α * ê * γ
对于头18.31(ê = 0.99):
v_debiased = [0.5, 1.2, -0.3] + 20 * 0.99 * [0.4, 0.4, -0.2]
= [0.5, 1.2, -0.3] + 19.8 * [0.4, 0.4, -0.2]
= [0.5, 1.2, -0.3] + [7.92, 7.92, -3.96]
= [8.42, 9.12, -4.26]




















 2578
2578

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








