红黑树的插入

最新推荐文章于 2021-11-28 12:02:37 发布

原创最新推荐文章于 2021-11-28 12:02:37 发布 · 1.2k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #java

Java数据结构与算法专栏收录该内容

10 篇文章

订阅专栏

本文详细介绍了红黑树的定义、性质以及插入操作。红黑树是一种自平衡二叉查找树，插入操作中，新节点默认为红色，通过着色和旋转策略确保树的平衡，保持查找、插入、删除的时间复杂度为O(logn)。文章通过实例展示了不同插入情况下的调整过程。

文章目录

红黑树定义
红黑树性质
红黑树的插入

红黑树定义

红黑树(Red Black Tree) 是一种自平衡的二叉查找树，典型用途是实现关联数组，红黑树与AVL树类似，都是在插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

红黑树查找、插入删除的时间复杂度为O（logⁿ）

下图是一棵红黑树：

在这里插入图片描述

红黑树性质

红黑树是每个节点都带有颜色属性的二叉查找树，颜色是红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

每个节点是红色或黑色
根节点时黑色
哨兵节点是黑色（且每个叶节点都要指向一个哨兵节点，哨兵节点一定是黑的）
每个红色节点的两个子节点是黑色。（从每个节点到根的所有路径上，不能有两个连续的红色节点）
从任一节点到其叶子节点的所有路径都包含相同数据的黑色节点

这些约束强制了红黑树的关键性质：从根到叶子的最长路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的

在二叉树中，每次插入的节点都是红色，至于该节点最后是什么颜色，取决于把不同的情况。

红黑树的插入

红黑树的插入，每次新插入的节点都是红色的，但是最终是什么颜色，取决于以下情况：

记要插入的节点为：p

① 如果p是第一个节点，根据红黑树性质：根节点必须为黑色。所以该节点的颜色为黑色。

② 若p的双亲节点的颜色为红色，则需要通过旋转或者着色的方式，进行红黑树的调整。

注意，这里又分为两种情况：(1).若p插入到双亲节点的右侧。 (2) 若p插入双亲节点的左侧。

通过以上方式，我们可以进行红黑树的调整，可是我们如何知道什么情况下使用旋转的方式，什么情况下使用着色的方式呢？

当p的双亲的双亲的左（右）孩子为红色时，我们通过着色的方式，进行调整，即让p的双亲的双亲的左右孩子变为红色，p的双亲的双亲变为黑色，这样我们就能保证，在红黑树的每一条路径上的黑节点的个数都是相等的。
当p的双亲的双亲的左（右）孩子为黑色时，我们通过旋转的方式，进行调整。有可能是双旋转，也有可能是单旋转，这取决于p插入在其直接双亲节点和p双亲的双亲节点的颜色，从而达到每一条路径上的黑节点个数是相等的。

我们上述所说的p双亲的双亲的左(右)孩子，这个左和右，说的是从整体上看，p在红黑树的左边插入还是右边插入，如果是从左边插入，则找的几居室双亲的双亲的右孩子，反之亦然。

示例：

注意：p指向的是待插入节点，在演示的过程中，前面的没有将哨兵节点截进图内，但是一定要清楚，每一个新插入的节点的左右孩子最开始都是指向哨兵节点的。且哨兵节点一定是黑色的。

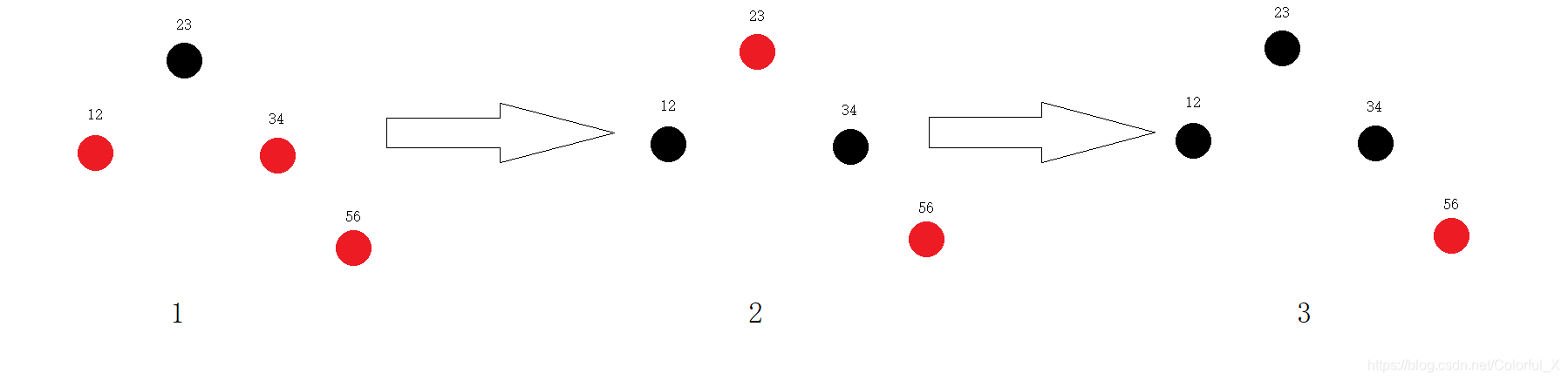
① 现在p是值为12的节点，插入后发现p是根节点，所以p的颜色必须为黑色。

在这里插入图片描述

② 现在p是值为23的节点，它应该插入12的右侧。p的父节点是黑色，且每条路径上的节点数相同，也没有出现一条路径上同时出现连续两个红色节点的情况，所以正常插入(新插入的节点都是红色的)。如下图：

在这里插入图片描述

③ 现在p是值为34的节点，应该插入23的右侧。 p(34)的父节点为红色，此时出现了连续两个红节点的情况，这个时候，我们就需要看p的双亲的双亲节点的左孩子节点是什么颜色，我们知道，此时12这个节点的左孩子是哨兵节点，而哨兵节点是黑色的，所以我们要通过旋转的方式，调整这棵红黑树。我们发现，p(34)和23、12这三个节点在同一直线上，所以采用左单旋转的方式进行调整，调整后，为了保持在每一条路径上黑色节点的个数相同，我们需要将p的双亲节点置为黑色，把p的双亲的双亲节点置为红色。如下图：
在这里插入图片描述
④ 现在p是值为56的节点，应该插入34的右侧。p(56)的父节点为红色，此时又出现了同一路径上连续两个红节点的情况，这个时候，我们又要去看p的双亲的双亲节点(即23这个节点)的左孩子节点是什么颜色，从上图的，我们得到该节点的颜色是红色，于是我们就可以通过着色的方式进行红黑树的调整，还记得我们是怎么着色的吗？将p的双亲的双亲节点变为红色，然后将p的直接是双亲和p的双亲的双亲的左孩子节点变为黑色。但是，这里我们要注意一点就是，我们将p的双亲的双亲节点变为红色了，此时p的双亲的双亲节点是我们整颗二叉树的根节点，根据红黑树的性质，根节点永远是黑色，我们又要将p的双亲的双亲节点变回黑色。

        修改完后，我们让p指向p的双亲的双亲，继续看p的双亲是否为红色，如果是，则继续调整(调整规则和③④相同，这里为什么要将p指向p的双亲的双亲呢？这是因为如果我们现在插入p，这个p的双亲的双亲节点不是根节点，那么我们通过着色的方式后，会将p的双亲的双亲节点变为红色，我们就不能保证在p的双亲的双亲节点作为子节点的那颗二叉树中，其父节点是红色还是黑色。所以要再次进行判断。)，如果不是，则不调整。
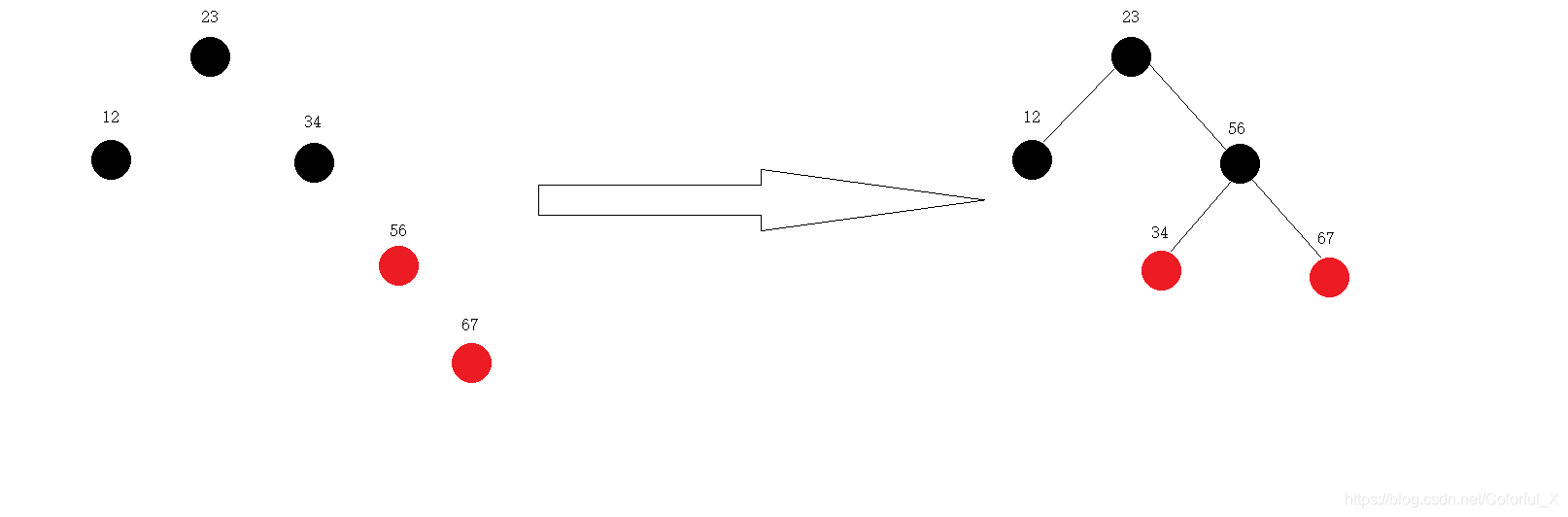
在这里插入图片描述
        ⑤ 继续插入，p现在是值为67的节点，应该插入56的右侧，p(67)的父节点为红色，又出现了两个连续红色节点的情况，我们按照之前的规则，寻找p的双亲的双亲的左孩子节点，发现p的双亲的双亲节点的左孩子指向哨兵节点为黑色，我们通过左单旋转的方式调整红黑树，并将p的双亲置为黑色，p的双亲的双亲节点置为红色。如下图所示：
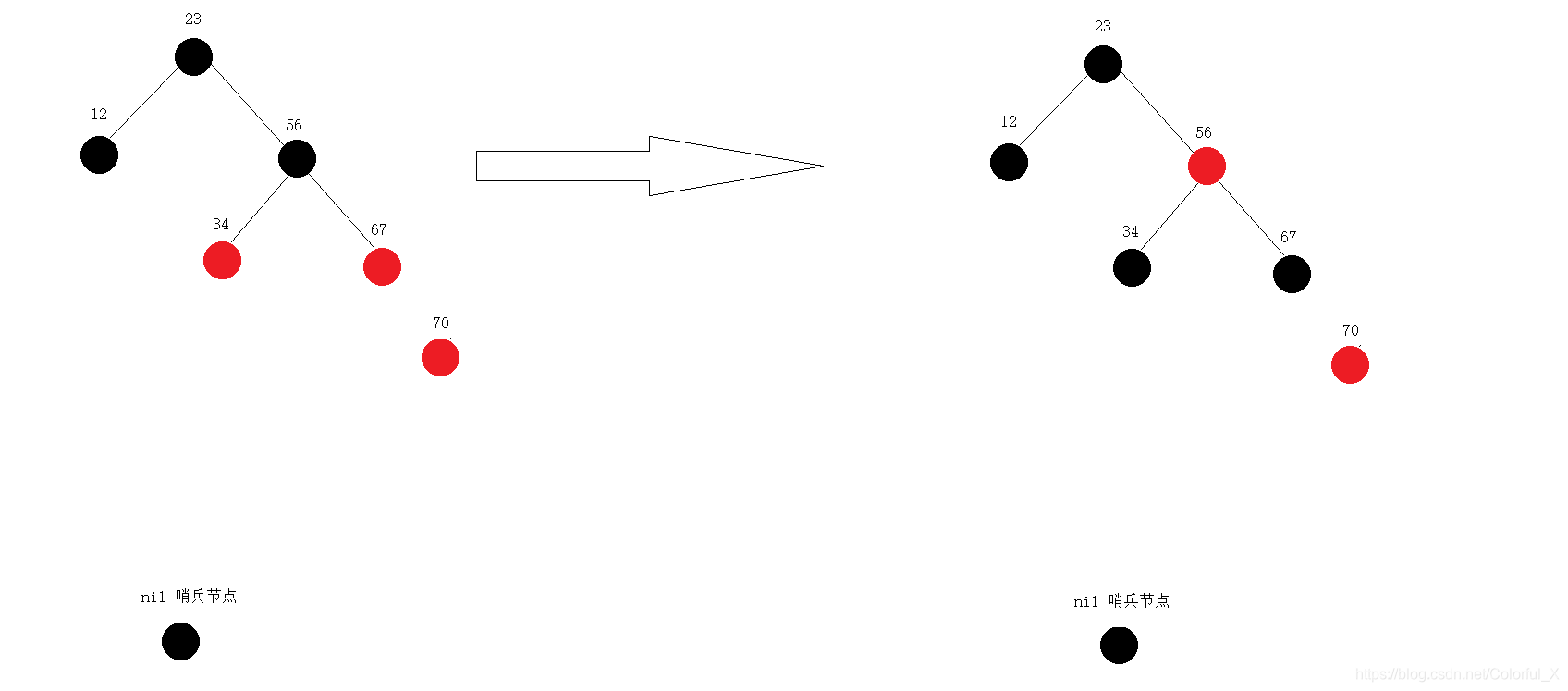
在这里插入图片描述
        ⑥ 继续插入，p现在是值为70的节点，应该插入67的右侧,p(70)的父节点为红色，我们又要寻找p的双亲的双亲的左孩子节点，发现是红色，于是我们通过着色方式进行调整，调整后，将p指向p的双亲的双亲，则p新指向的节点为56，再去判断56的双亲是不是红色，如下图，发现56的双亲不是红色，则不用再调整：
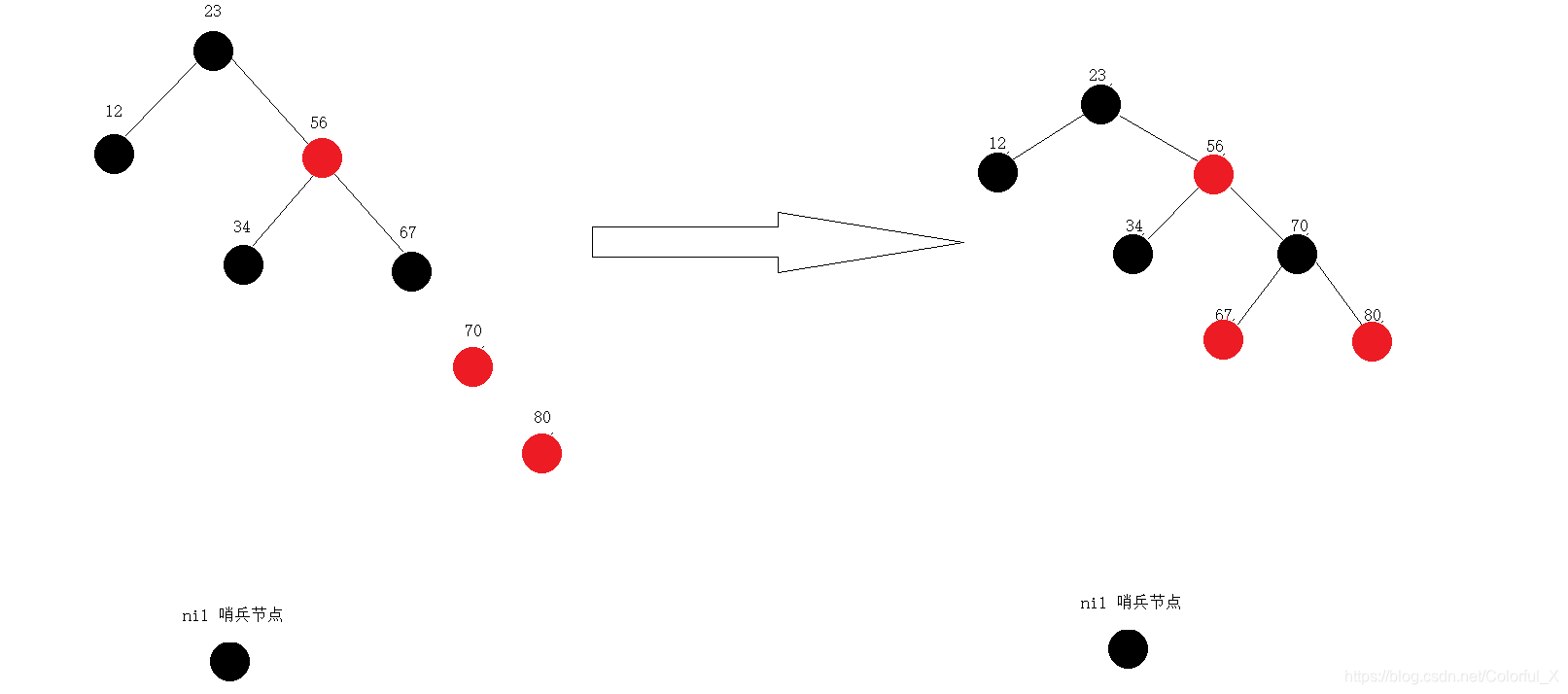
在这里插入图片描述
        ⑦ 继续插入，p现在是值为80的节点，应该插入70的右侧，p(80)的父节点为红色，按照之前的规则，寻找p的双亲的双亲的左孩子，发现是黑色，则通过旋转的方式进行调整：

在这里插入图片描述
        ⑧ 继续插入，p现在是值为76的节点，应该插入80的左侧，p(76)的父节点为红色，按照之前的规则，我们寻找p的双亲的双亲的左孩子，发现是红色，通过着色的方式。此时p指向了70这个节点，其父节点是红色，所以，我们还需要再次进行调整，寻找70这个节点的双亲的双亲节点的左孩子，发现是黑色，于是通过单旋转的方式调整。如下图：
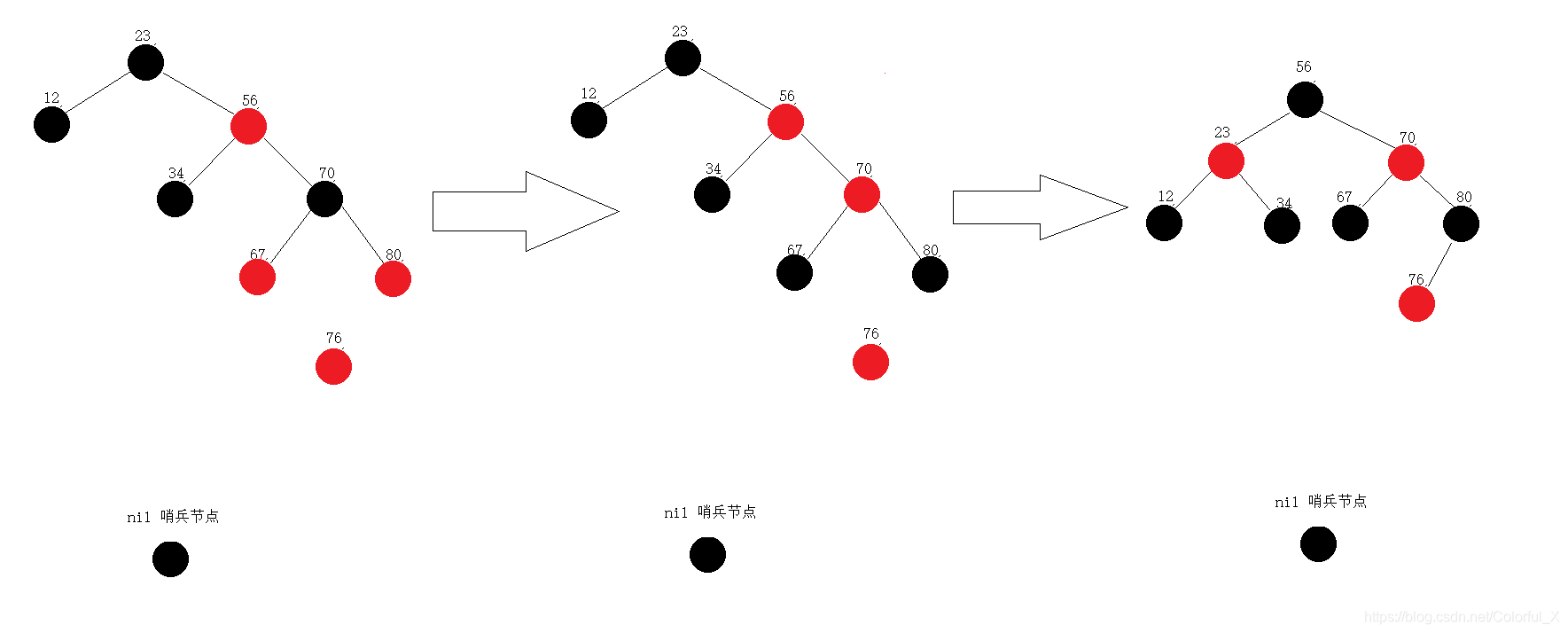
在这里插入图片描述
        ⑨ 继续插入，p现在是值为90的节点，应该插入80的右侧，p(90)的父节点为黑色，所以照常插入即可。

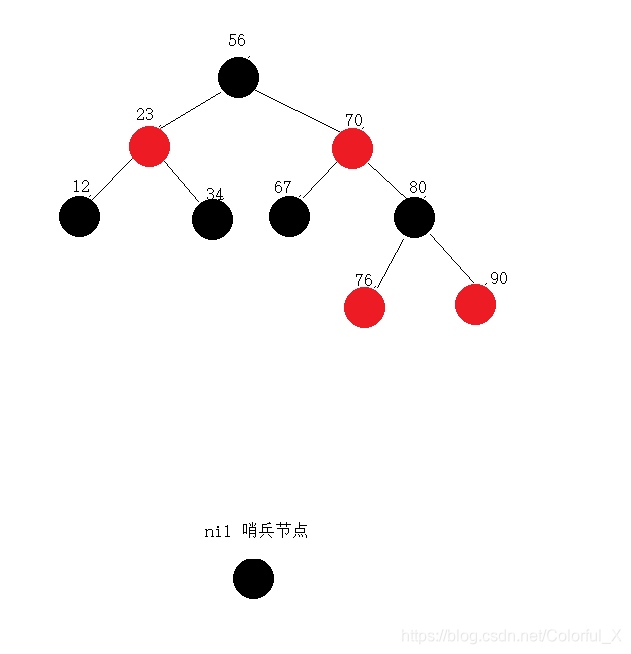
        以上我们没有涉及到双旋转的情况，下面，我们涉及到了双旋转：

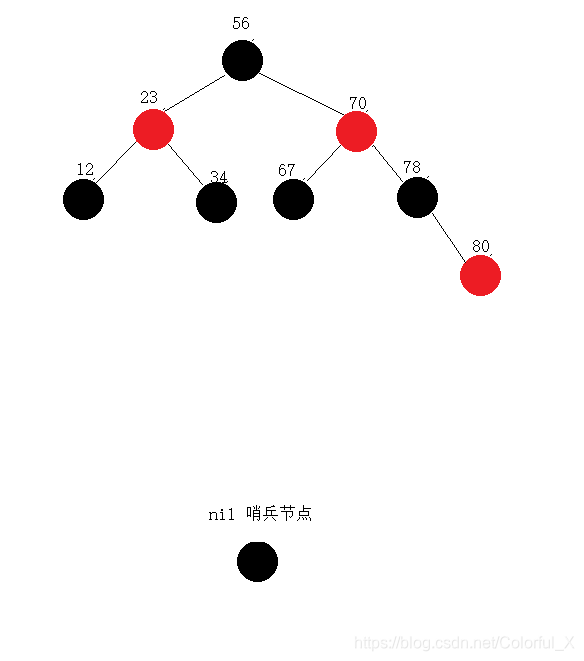
在这里插入图片描述
按照上图，继续插入，p现在是值为79的节点，应该插入80的左侧，p(79)的父节点为80为红色，找到p的双亲的双亲节点78的左孩子节点为哨兵节点，是黑色，所以要通过旋转的方式，但是由于79、80、78 这三个节点不在同一直线上，所以我们需要用到双旋转，先右单旋，后左单旋。

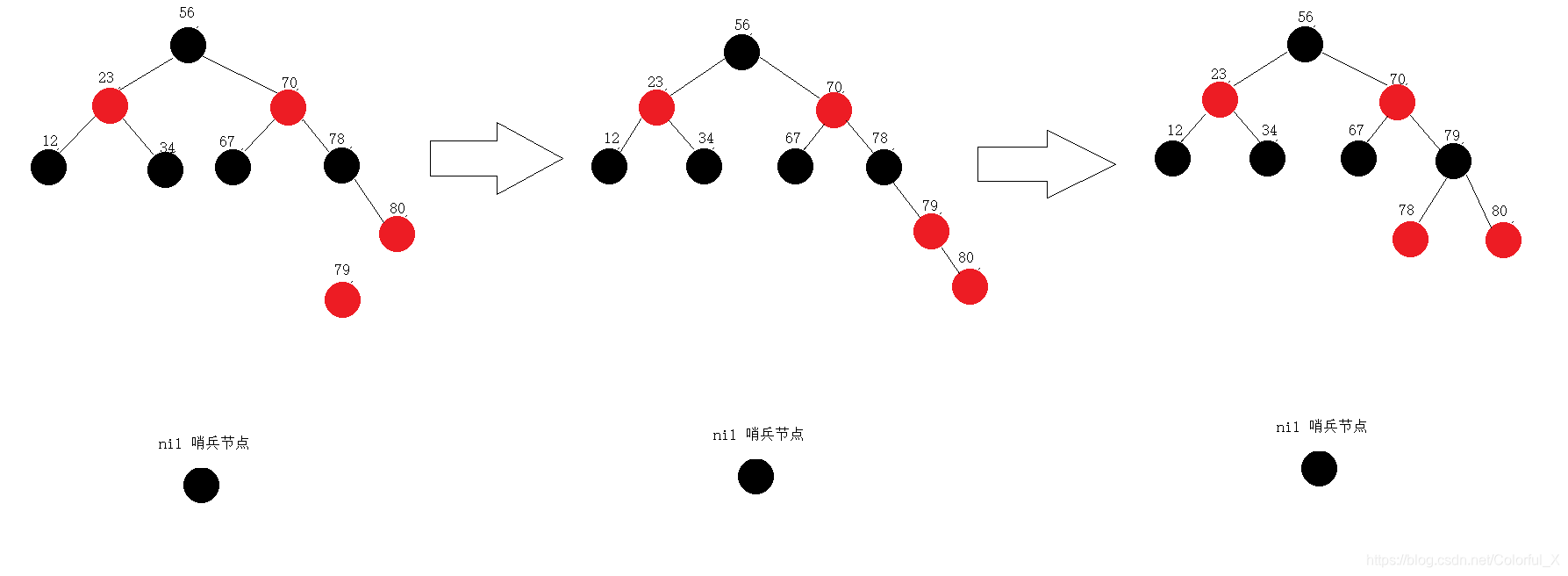
在这里插入图片描述
代码实现：

boolean insert(int kx){
        rb_node p = new rb_node(kx);
        p.leftChild = p.rightChild = nil;
        p.color = colorType.RED;
        adjust1(p);
        return true;
    }

 private void adjust(rb_node p){
        // 如果双亲节点存在，并且双亲节点的颜色是红色，我们就需要调整树。
        // 至于怎么调整（旋转还是着色，需要看双亲的双亲的另一个孩子节点是什么颜色）
        while(p.parent!=null && p.parent.color== colorType.RED){
            // 如何判断是双亲的双亲的左边 还是 双亲的双亲的右边
            // 插入的节点在双亲的双亲的右边
            if (p.parent.parent.rightChild == p.parent){
                rb_node left = p.parent.parent.leftChild;
                // 双亲的双亲的左边节点是红色，则把双亲的双亲的左右子节点的颜色变为黑色
                if (left.color == colorType.RED){
                    p.parent.color = colorType.BLACK;
                    left.color = colorType.BLACK;
                    p.parent.parent.color = colorType.RED;
                    // 将双亲的双亲置为红色后，我们还需要看这个节点的双亲是否为红色
                    p = p.parent.parent;
                }else{
                    // p挂在直接双亲的左边，需要双旋
                    if(p.parent.leftChild == p){
                        p = p.parent;
                        rotateRight(p);
                    }
                    p.parent.color = colorType.BLACK;
                    p.parent.parent.color = colorType.RED;
                    rotateLeft(p.parent.parent);
                }
            }else{ //插入节点在左边
                rb_node right = p.parent.parent.rightChild;
                if(right.color == colorType.RED ){
                    p.parent.color = colorType.BLACK;
                    right.color = colorType.BLACK;
                    p.parent.parent.color = colorType.RED;
                    p = p.parent.parent;
                }else{
                    if(p.parent.rightChild == p){
                        p = p.parent;
                        rotateLeft(p);
                    }
                    p.parent.color = colorType.BLACK;
                    p.parent.parent.color = colorType.RED;
                    rotateRight(p.parent.parent);
                }
            }
        }
    }