Softmax函数下的交叉熵损失含义与求导

交叉熵损失函数(CrossEntropy Function)是分类任务中十分常用的损失函数，但若仅仅看它的形式，我们不容易直接靠直觉来感受它的正确性，因此我查阅资料写下本文，以求彻底搞懂。

1.Softmax

首先是我们的softmax函数。
它很简单，以一个向量作为输入，把向量的每个分量，用指数函数归一化后输出。具体来说，其数学形式为：
$$softmax(x_i)=\frac{e^{x_i}}{{\sum }_k{e}^{x_k}}$$
$x_i$为向量中第i个项。

设$softmax$的输出向量为$input\_vector$，当$input\_vector$中某个分量过大时，可能导致其指数形式数值过大溢出。因此我们需要将$input\_vector$每一项减去$max(input\_vector)$，再输入$softmax$中去。可以验证，减去最大值后，$softmax$的输出不会改变。

2.交叉熵损失函数

交叉熵损失函数作为分类任务最常用的$lossfunction$，我们理应深刻理解并熟知其形式与含义。

2.1 交叉熵为什么能衡量分类结果的好坏？

这是交叉熵损失函数的公式：
$$Loss=-\sum _i{y}_{i}log{a}_i$$
其中，$a_i$为softmax函数输出向量的第$i$个分量，$y_i$为样本真实标签的$onehot$形式的第i个分量。
也就是说，实际上求和的项中只有一个不为0，$Loss$就等于$-log{a}_k$，其中k对应的是样本的真实标签。

根据对数函数的性质，容易得出$-log{a}_k$随$a_k$增大而减小。也就是说，$softmax$输出向量对应$label$的那项越大，$Loss$就越小，这正是我们希望的。

*2.2 熵、交叉熵（选读）

2.2.1 自信息

自信息是用来量化信息量大小的值。可以这样认为，越让我们觉得惊讶的事情带来的信息量越大。
一个优生考出好成绩的概率很大，当他期末成绩优秀时我们不会感到奇怪。但当一个学习很差的同学考得很好，我们就会感到非常惊讶。前者发生时，我们难以挖掘出隐含信息，而后者发生时，我们会推测这名学生可能有作弊行为，抑或他近期学习用功，找到了高效的学习方法。这样来看，后者带来的信息量明显大于前者。也就是说，概率更小的事情的发生能带来更多的信息。自然地，我们可以用概率来衡量自信息，公式如下：
$$s=log(1/p_i)=-log{p}_i$$
其中$p_i$是事件i发生的概率。

2.2.2 熵

熵，即为包含信息量的大小。对于一个事件（如分类），它的结果有很多种（如分为狗、猫…），分别对应不同的概率。很自然的，我们用各个结果自信息的加权平均作为事件的熵。
假设有n个结果（如分类有n类），则可以写成:
$$e=-\sum _i{p}_{i}log{p}_i$$

2.2.3 交叉熵

交叉熵和熵是类似的概念，区别在于，现在我们是对两个不同分布进行定义。离散型变量的交叉熵可定义为：
$$H=-\sum p_{i}log{q}_i$$
可以理解为，每个结果的实际概率为$p_i$，却有人将概率估计为$q_i$。(当前样本分为类i的真正概率为$p_i$，但是分类器认为该样本为第i类的概率是$q_i$）。也就是说，我们带着某个主观认知去接触某个客观随机现象的时候，会产生的平均自信息量。
当我们主观上认为一个事情发生的概率很低（即$-log{q}_i(x)$很大），但是客观上发生概率$p_i$很大的时候，也就是主观认知和客观现实非常不匹配的时候，交叉熵的结果会很大。

交叉熵衡量了两个概率分布的差异。其值越大，两个概率分布相差越大；其值越小，则两个概率分布的差异越小。

从概率论角度来讲，我们要让分类器结果好，就是要让输出的各类的概率分布与真实分布接近，也就是要优化交叉熵，让其尽量小。

2.2.4 Kullback-Leibler Divergence(K-L 散度)

交叉熵可以衡量我们基于某种主观认识去感受客观世界时，会产生的平均自信息量。但是根据上面的公式，即使主观和客观完全匹配（交叉熵等于信息熵），只要事件仍然随机而非确定，产生的自信息量就一定大于0。那我们应该如何更好地度量主观认识和客观事实之间差异呢？可以用当前对事件的主观认识产生的期望和完全正确认识事件时产生的期望的差值来衡量，也就是相对熵（常称作KL-散度），通常写作：

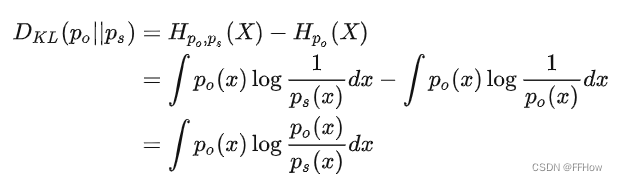
当我们的主观认知完全匹配客观现实的时候，KL-散度应该等于0，其它任何时候都会大于0。

由于存在恒为正这一性质，KL-散度经常用于描述两个分布是否接近，也就是作为两个分布之间“距离”的度量；不过由于运算不满足交换律，所以有不能完全等同于“距离”来理解。

机器学习中通常直接用交叉熵作为损失函数的原因在于，客观分布并不随模型参数变化而变化，所以即使是优化KL-散度，对参数求导后就只剩下交叉熵的导数了。

3. 交叉熵损失求导（梯度计算）