Leetcode Hot100|96.不同的二叉搜索树 Python

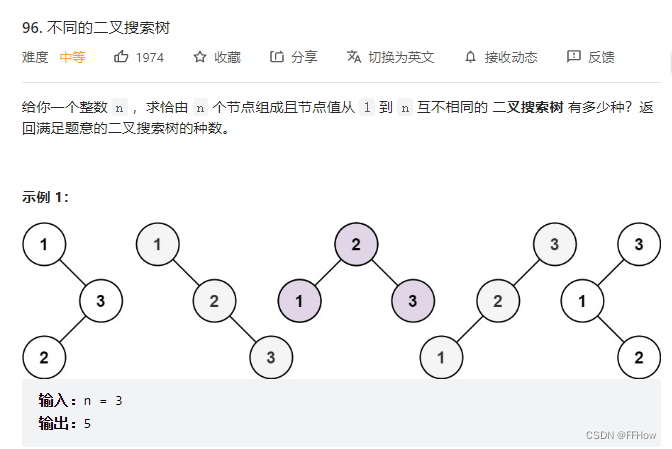
题目如上，题意很好理解。
这道题关键是要熟悉二叉搜索树的一个关键性质，即若某个节点的左子树不为空，则左子树所有节点的值小于根节点的值，若他的右子树不为空，则右子树上所有节点都小于根节点的值。

有了这个性质，我们很容易有这样一种想法——尝试对二叉搜索树选择某个根节点进行划分为左右子树，则当前二叉搜索树的种类数等于左子树的种类乘右子树的种类。

借助动态规划，加上刚才提到的思路，我们便能很自然地提出解法。

代码实现如下：

class Solution(object):
    def numTrees(self, n):
        """
        :type n: int
        :rtype: int
        """
        mat = [[1 for i in range(n)] for j in range(n)]

        for l in range(1, n):  #对距离进行遍历，以便依次访问对角线
            for start in range(n - l):
                end = start + l
                val = 0
                for k in range(start, end + 1):  #选根节点
                    left = mat[start][k - 1] if k > start else 1
                    right = mat[k + 1][end] if k < end else 1
                    val += left * right
                mat[start][end] = val
        # print(mat)
        return mat[0][n - 1]

最后结果：