leetcode 113、Path Sum II,难度medium
0. 题干
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,

1. 代码
class Solution {
private:
vector<vector<int>> ans;
vector<int> t;
public:
void findPath(TreeNode* root,int sum){
if(!root) return;
t.push_back(root->val);
if(!root->left && !root->right && root->val==sum) ans.push_back(t);
findPath(root->left,sum-root->val);
findPath(root->right,sum-root->val);
t.pop_back();
//pop_back删除向量容器最后一个成员
}
vector<vector<int>> pathSum(TreeNode* root, int sum) {
findPath(root,sum);
return ans;
}
};
2 代码流程
这个代码流程详细说下,用了之前没整过的思想,叫做回溯算法。
2.1 啥叫回溯算法?
我们可以理解为通过选择不同的岔路口寻找目的地,一个个岔路口一个岔路口的去尝试找到目的地。
如果走错了路,继续返回来找到岔路口的另一条路,直到找到目的地。
(描述参考):https://www.jianshu.com/p/dd3c3f3e84c0
2.2 举例说明
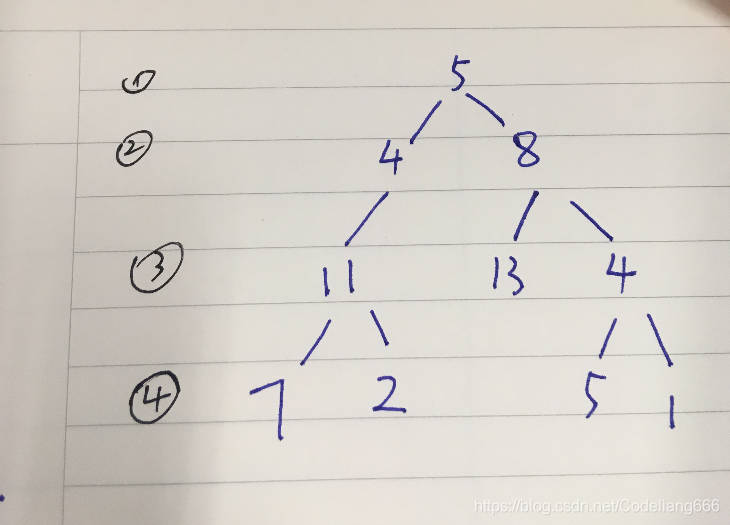
就以题干的树为例子,目标和sum为22,这颗树共四层;以下为了描述方便,直接把结点值描述为结点的名称。
先存root结点5,到一维指针数组t里面,sum值减5,进入结点4,sum值再减去4,进入结点11,sum值再减去11,
结点11,然后进入 结点11的左节点7,此时sum值22-5-4-11=2不 为7,由于结点7的左右孩子都为NULL,此时递归return,
返回到第四层,继续返回到第三层,并且把7从一维数组里面删除掉(回溯);进入结点11的右孩子2,满足要求,于是把存储了
[5,4,11,2]的数组存到ans里面;
接下来不断递归return,t只剩下值5;sum值减5进去结点8,再减8进去左孩子结点13,此时22-5-8=9,不符合要求;
清除数组t里面的值13,递归回到结点8,然后进入结点4,sum继续减4;sum=22-5-8-4=5,
发现[5,8,4,5]符合要求,于是存到 ans数组里面; 回溯删除5,回到结点4.发现右孩子1不满足要求;
最终满足要求的是[5,4,11,2]和[5,8,4,5],已被依次存到ans里面,问题OVER!





 本文解析了LeetCode上编号为113的题目PathSum II,难度等级为中等。该题要求在给定的二叉树中寻找所有从根节点到叶子节点的路径,这些路径的总和等于给定的目标和。文章详细介绍了使用回溯算法解决此问题的方法,通过示例清晰展示了算法的执行流程。
本文解析了LeetCode上编号为113的题目PathSum II,难度等级为中等。该题要求在给定的二叉树中寻找所有从根节点到叶子节点的路径,这些路径的总和等于给定的目标和。文章详细介绍了使用回溯算法解决此问题的方法,通过示例清晰展示了算法的执行流程。
















 13万+
13万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








