【链表】LeetCode #141环形链表（快慢指针）

题目链接：

LeetCode #141环形链表

题目描述：

#141. 环形链表

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

通过次数198,552 提交次数406,539

分析：

环形链表是链表问题中的基础，注意示例中的输入为链表和 pos，但 给出的函数参数只有链表。

该题可用 双指针 解决：

• 设置快慢指针 i, j；
• 快指针 i 每次走 2 步，慢指针 j 每次走1步；
• i, j 都从链表的第一个节点开始走；
• 如果 i, j 能够再次相遇，说明链表有环。

代码：

提交截图：

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
 /*
 * 看给出的函数，并不会把 pos 传进来
 * 该题在小灰的《漫画算法》上有，用快慢指针
 * 快指针一次走两步，满指针一次走一步
 * 当两个指针再次相遇，说明链表有环
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode i = head, j = head;
        while(i != null && i.next != null && j != null){
            i = i.next.next;
            j = j.next;
            if(i == j) return true;
        }
        return false;
    }
}

扩展：

如果知道了是 环形链表，如何 求入环点？

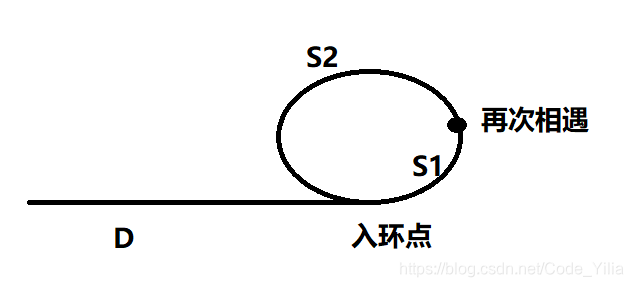
其中，
D： 链表头到入环点的距离；
S1： 入环点到快慢指针再次相遇的距离；
S2： 再次相遇的位置走完环形再次到达入环点的距离。

因为链表有环，快慢指针会 再次相遇，此时快指针 i 和慢指针 j 分别走了多远？

• 慢指针 j 走了 D + S1；
• 快指针 i 走了 D + 2S1 + S2；
• 因为 i 每次走 2 步，j 每次走 1 步，所以 i 走的距离是 j 的两倍，
• 得到 2 * (D + S1) = D + 2S1 + S2 ，推出 D = S2；

故想要求得入环点，只需要在 i, j 再次相遇时，将 其中一个指针指向表头，二者以 同样的速度 向后走，当两个指针 又一次相遇 时，便是入环点。