【动态规划】 LeetCode #338 比特位计数（时间复杂度 O(n)）

题目链接：

LeetCode #338 比特位计数

题目描述：

#338.比特位计数
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例 1:

输入: 2
输出: [0,1,1]
示例 2:

输入: 5
输出: [0,1,1,2,1,2]
进阶:

给出时间复杂度为O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗？
要求算法的空间复杂度为O(n)。
你能进一步完善解法吗？要求在C++或任何其他语言中不使用任何内置函数（如 C++ 中的 __builtin_popcount）来执行此操作。
通过次数38,350 | 提交次数51,040

隐藏提示：

分析：

先来看看 0~31 对应二进制中 “1” 的个数：

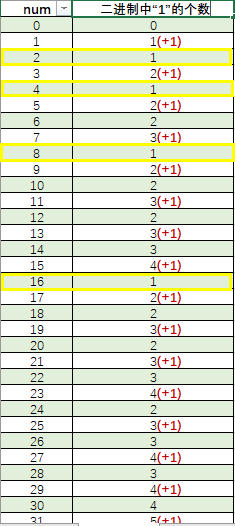
我们很容易发现以下几个规律：

① 2 的整数次幂对应的二进制只有最高位是 “1”，其他均为 “0”，即 2 的整数次幂对应二进制中 “1” 的个数为 1。

②表中的红色 “(+1)” 表示对应二进制中 “1” 的个数比上一行增加了 1，可以看到每逢奇数，对应二进制中 “1” 的个数会增加。这一点也很容易理解，比如 “6” 对应二进制为 “0110”，而 “7” 对应二进制为 “0111”，说到底十进制 +1，在二进制也加 1，而奇数是由偶数 +1 而来，偶数对应二进制最后一位为 “0”，所以二进制 +1 后会把原本末位的 “0” 变成 “1”，所以对应二进制中 “1” 的个数自然也多了一个。

③根据提示我们知道，可以把数分成奇偶两种情况来考虑。目前奇数已经考虑完了，偶数中是 2 的整数次幂的也考虑完了，下面来看其他的偶数：

偶数是怎么来的呢？

偶数 = 某个数 * 2，即某个数左移1位，末位补0

也就是说，偶数对应二进制中 “1” 的个数和其除以 2 的数对应二进制中 “1” 的个数是相同的（除 2 的整数次幂外）。

我们可以用动态规划来解题，设 dp[i] 为 i 的二进制中 1 的个数。状态转移方程式如下：

i 为 2 的整数次幂时（(i & i-1) == 0），dp[i] = 1;

i 为其他偶数时（(i & 1) == 0），dp[i] = dp[i / 2]；

i 为奇数时，dp[i] = dp[i - 1] + 1。

代码：

/*
*动态规划，设 dp[i] 为 i 的二进制中 1 的个数
*首先，2 的整数次幂的二进制中必然只有 1 个 1
*其他的呢？根据提示，可以从奇偶来考虑
*偶数是怎么来的呢？偶数 = 某个数 * 2，即某个数左移1位，末位补0，故 dp[i] = dp[i / 2]
*当 i 为奇数时呢？写出来了 0-31 对应二进制中 1 的个数，
*可以发现：到奇数的时候 1 的个数会增加，即 dp[i] = dp[i - 1] + 1
*如何判断奇偶：(偶数 & 1) == 0，(奇数 & 1)  == 1
*/
class Solution {
    public int[] countBits(int num) {
        int[] dp = new int[num + 1];
        dp[0] = 0;
        for(int i = 1; i <= num; i++){
            if((i & i-1) == 0){// i 是 2 的整数次幂，对应二进制中只有最高位为1
                 dp[i] = 1;
            }else if((i & 1) == 0){//当 i 为偶数时
                dp[i] = dp[i / 2];
            }else{
                dp[i] = dp[i - 1] + 1;
            }
        }
        return dp;
    }
}

算法时间复杂度为 O(n)，空间复杂度为 O(n)。