【动态规划】 LeetCode #303 区域和检索 - 数组不可变

题目链接：

LeetCode #303 区域和检索 - 数组不可变

题目描述：

#303. 区域和检索 - 数组不可变
给定一个整数数组 nums，求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和，包含 i, j 两点。

示例：

给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange()

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
说明:

你可以假设数组不可变。
会多次调用 sumRange 方法。
通过次数38,254 | 提交次数62,258

解决方案：

我们先考虑给我们一个数组，要这么求 i 到 j 的和？直接暴力求解肯定是超时的，(i, j) 的和可以用 (0, j) 的和减去 (0, i) 的和再加 nums[i]，满足动态规划的条件，设 sums[i] 为前 i 个数的和，包含第 i 个数：

sums[0] = nums[0]，这里表示第一个数的和，因为下标从0开始

sums[i] = sums[i-1] + nums[i]

返回的结果是 sums[j] - sums[i] + nums[i]

再来看给的初始代码：

class NumArray {

    private int[] sums;

    public NumArray(int[] nums) {

    }
    
    public int sumRange(int i, int j) {

    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(i,j);
 */

我们要在 sumRange() 方法里返回和，但是这个方法获取不到 nums[i]，所以我们可以把“return sums[j] - sums[i] + nums[i]”改为“return sums[j] - sums[i - 1]”。

理论上来说用 (0, j) 的和减去前 (0, i) 的和确实等于 (i, j) 的和，但是当 i = 0 时，sums[i - 1] 就会越界，其实当 i = 0 时，也就是 (0, j) 的和，即 sums[j]。

另一个坑在于题目描述中的说明：“会多次调用 sumRange 方法”，什么意思呢？

你的测试用例有可能是这样的：[“NumArray”,“sumRange”,“sumRange”,“sumRange”]
[[[-2,0,3,-5,2,-1]],[0,2],[2,5],[0,5]]

到此时提交的代码如下（这个代码是会报错的！）：

/*
*测试用例"会多次调用 sumRange 方法"
*比如：[[[-2,0,3,-5,2,-1]],[0,2],[2,5],[0,5]]
*动态规划,设 sums[i] 为前 i 个数的和，包含第 i 个数
*sums[0] = nums[0]（这里表示第一个数的和，因为下标从0开始）
*sums[i] = sums[i-1] + nums[i]
*返回的结果是 sums[j] - sums[i-1]
*/
class NumArray {

    private int[] sums;

    public NumArray(int[] nums) {
        sums = new int[nums.length];
        sums[0] = nums[0];
        for(int i = 1; i < nums.length; i++){
            sums[i] = sums[i - 1] + nums[i];
        }
    }
    
    public int sumRange(int i, int j) {
        if(sums.length == 0 || i  < 0 || j < 0) return 0;
        if(i == 0) return sums[j];
        return sums[j] - sums[i - 1];
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(i,j);
 */

通过提交结果，我们可以发现第三个坑…

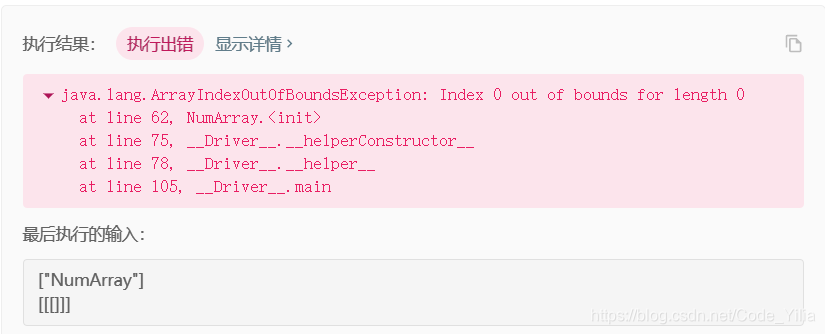
最后通过看官方题解，发现官方选择了返回的不是 sums[j] - sums[i - 1]，而是 sums[j + 1] - sums[i]，也就是说建 sums[nums.length + 1]，然后下标为 0 的不用，从下标为 1 开始，这就是题解的魅力吧…让你感觉哇还可以这么改的，但是感觉自己没吃透，这个题还是值得反复看的，不然以后遇到了自己还是想不出来。

代码：

/*
*测试用例"会多次调用 sumRange 方法"
*比如：[[[-2,0,3,-5,2,-1]],[0,2],[2,5],[0,5]]
*动态规划,设 sums[i] 为前 i 个数的和，包含第 i 个数
*sums[0] = nums[0]（这里表示第一个数的和，因为下标从0开始）
*sums[i] = sums[i-1] + nums[i]
*返回的结果是 sums[j] - sums[i-1]
*/
class NumArray {

    private int[] sums;

    public NumArray(int[] nums) {
        sums = new int[nums.length + 1];
        for(int i = 0; i < nums.length; i++){
            sums[i + 1] = sums[i] + nums[i];
        }
    }
    
    public int sumRange(int i, int j) {
        if(sums.length < 2 || i  < 0 || j < 0) return 0;
        return sums[j + 1] - sums[i];
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(i,j);
 */