题目链接:
题目描述:
300.最长上升子序列给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
解决方案:
本题可以用动态规划解决,注意题目中的最长上升子序列可能不是连续的。动态规划的重点依然是:①如何设置dp[i];②状态转移方程式。
我们设dp[i] 为以 nums[i] 为结尾的最长上升子序列的长度,若 nums[i] 小于前面的所有元素:dp[i] = 1;若 nums[i] 前面有小于 nums[i] 的元素,可能是一个或多个:
dp[i] = max(dp[j], dp[k], dp[l]…) + 1,
当 nums[j] < nums[i]
nums[k] < nums[i]
nums[l] < nums[i] …时。
第一次提交:

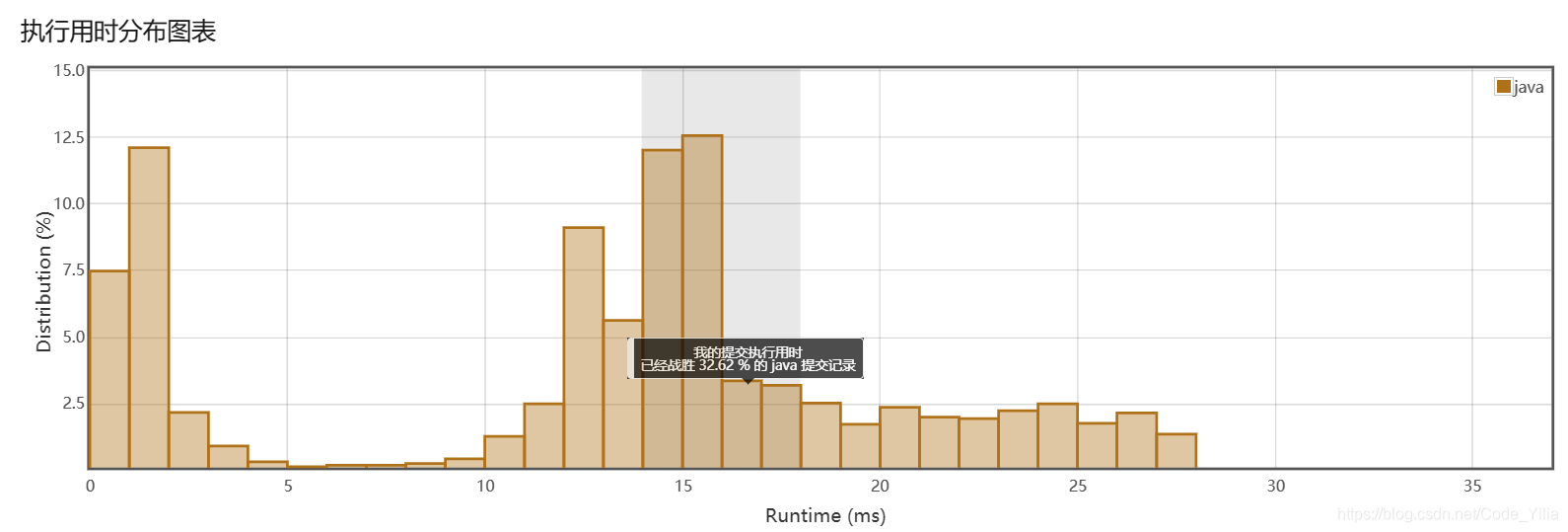
代码:
/*
*动态规划,注意到最长上升子序列可能是不连续的
*设 dp[i] 为以 nums[i] 为结尾的最长上升子序列的长度
*若 nums[i] 小于前面的所有元素:dp[i] = 1
*若 nums[i] 前面有小于 nums[i] 的元素,可能是一个或多个:
*dp[i] = max(dp[j], dp[k], dp[l]...) + 1
*条件:nums[j] < nums[i]
* nums[k] < nums[i]
* nums[l] < nums[i]
* ......
*/
class Solution {
public static int[] IndexOfSmaller(int[] nums, int current, int index){//返回nums[i]前面小于它的所有数的下标,此处current表示nums[i],index为i
int[] smaller = new int[index+1];//smaller[0]用来存放小于nums[i]的个数
int j = 0;//记录小于num[i]的个数
for(int i = 0; i < index; i++){
if(nums[i] < current){
smaller[j++] = i;
}
}
smaller[0] = j;//smaller[0]用来存放小于nums[i]的个数
return smaller;
}
public int lengthOfLIS(int[] nums) {
if(nums.length < 1) return 0;
int[] dp = new int[nums.length];
int result = 1;
for(int i = 0; i < nums.length; i++){
int[] smaller = IndexOfSmaller(nums, nums[i], i);
if(smaller[0] < 1){//nums[i] 小于前面的所有元素
dp[i] = 1;
}
else{
int max = dp[smaller[1]];
for(int j = 1; j < smaller.length; j++){
if(max < dp[smaller[j]]) max = dp[smaller[j]];
}
dp[i] = max + 1;
if(result < dp[i]) result = dp[i];
}
}
return result;
}
}
思想:既然要根据 nums[i] 前面是否有小于 nums[i] 的元素作为分情况讨论的基础,就单写一个方法,返回一个数组 smaller[],其中 smaller[0] 放小于 nums[i] 的元素的个数, 后面依次是每个小于 nums[i] 的元素下标。其他的按部就班,根据 smaller[0] 分类讨论,如果 nums[i] 前面的数都比它大,就返回1;否则,求出 max(dp[j], dp[k], dp[l]…),dp[i] = max + 1,最终的结果返回 max(dp[])。
优化:
优化:写代码的过程中就感觉自己做了很多的无用功,明明遍历一次可以做的事儿很多,我却好像每次遍历都完成了一丢丢的事儿。首先,我们想得到的只是长度,有必要把小于nums[i]的所有数都记录下来吗?当然不用,只去记录nums[i]前面所有比nums[i]小的元素的dp的最大值就够了。再者,是否必须得到nums[i]前面小于nums[i]的个数来作为分情况讨论的条件呢?如果个数为0,dp[i]固定为1;如果个数不为0,dp[i] = max + 1。完全可以给dp[i]赋初值:dp[i] = 1,如果个数为0,那么nums[i]前面所有比nums[i]小的元素的dp的最大值max=0,dp[i] = max + 1 = 1,虽然思想上是分情况讨论,但是代码里不必用if()条件判断一一对应。
优化后的代码:
/*
*动态规划,注意到最长上升子序列可能是不连续的
*设 dp[i] 为以 nums[i] 为结尾的最长上升子序列的长度
*若 nums[i] 小于前面的所有元素:dp[i] = 1
*若 nums[i] 前面有小于 nums[i] 的元素,可能是一个或多个:
*dp[i] = max(dp[j], dp[k], dp[l]...) + 1
*条件:nums[j] < nums[i]
* nums[k] < nums[i]
* nums[l] < nums[i]
* ......
*/
class Solution {
public static int MaxDpOfSmaller(int[] nums, int current, int index, int[] dp){//返回max(dp[j], dp[k], dp[l]...),此处current表示nums[i],index为i
int max = 0;
for(int i = 0; i < index; i++){
if(nums[i] < current && max < dp[i]){
max = dp[i];
}
}
return max;
}
public int lengthOfLIS(int[] nums) {
if(nums.length < 1) return 0;
int[] dp = new int[nums.length];
int result = 1;
for(int i = 0; i < nums.length; i++){
dp[i] = 1;
int max = MaxDpOfSmaller(nums, nums[i], i, dp);
dp[i] = max + 1;
if(result < dp[i]) result = dp[i];
}
return result;
}
}
第二次提交:

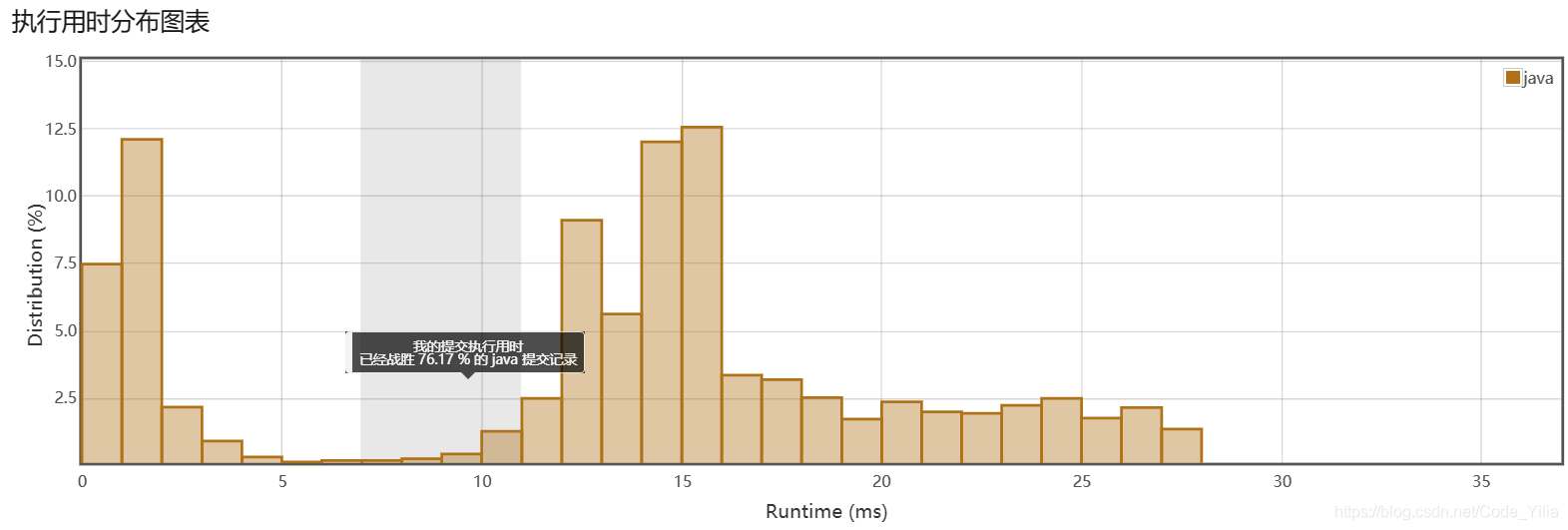
其他:
这个题目还有个进阶:你能将算法的时间复杂度降低到 O(n log n) 吗?
这个需要涉及到二分法,个人还是希望尽量按照算法的分类来刷题,有利于对某种算法思想的步步深入,就动态规划而言本题到这里可以告一段落了,后面做到二分法专题的时候会再尝试用二分法解决本题。







 本文详细解析LeetCode#300题——最长上升子序列的动态规划解法,通过示例讲解如何设定dp数组及状态转移方程,优化算法减少冗余操作,并提供代码实现。
本文详细解析LeetCode#300题——最长上升子序列的动态规划解法,通过示例讲解如何设定dp数组及状态转移方程,优化算法减少冗余操作,并提供代码实现。
















 1929
1929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








