目录
题目链接:203. 移除链表元素 - 力扣(LeetCode)
题目链接:24. 两两交换链表中的节点 - 力扣(LeetCode)
题目链接:19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
题目链接:142. 环形链表 II - 力扣(LeetCode)
1. 移除链表元素
题目链接:203. 移除链表元素 - 力扣(LeetCode)
题目描述:
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
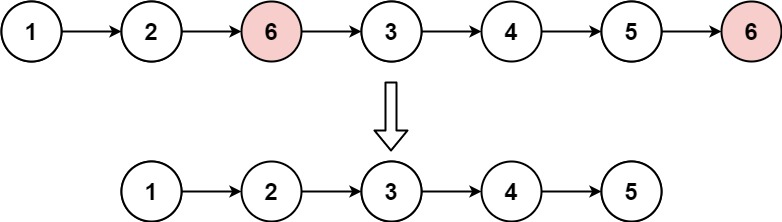
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
示例 2:
输入:head = [], val = 1
输出:[]
示例 3:
输入:head = [7,7,7,7], val = 7
输出:[]
思路提示(迭代):
为了简化边界条件的处理(例如删除头节点的情况),我们引入一个虚拟头节点 dummy,dummy.next 指向链表的头节点 listHead。
使用指针 current 从虚拟头节点 dummy 开始遍历链表。在遍历过程中,检查 current.next 的值是否等于目标值 targetValue。如果等于目标值,跳过该节点(即删除该节点);如果不等于目标值,移动指针到下一个节点。
代码实现(迭代):
class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}
class SolutionNew {
public ListNode removeNodesWithValue(ListNode listHead, int targetValue) {
// 创建虚拟头节点
ListNode dummy = new ListNode(0);
dummy.next = listHead;
ListNode current = dummy;
while (current.next != null) {
if (current.next.val == targetValue) {
// 跳过值等于目标值的节点
current.next = current.next.next;
} else {
// 移动到下一个节点
current = current.next;
}
}
return dummy.next;
}
} -
时间复杂度:O(n)
-
空间复杂度:O(1)
思路提示(递归):
链表题目常可以用递归的方法求解。具体实现思路如下:
-
递归条件:当遍历到链表末尾(当前节点为
null)时,直接返回null,终止递归。 -
递归处理后续节点:先深度优先递归处理当前节点的后续子链表,将处理后的链表头保存到
processedNext。 -
更新节点链接:将当前节点的
next指针指向处理后的后续链表头,确保后续节点已正确移除目标值节点。 -
判断当前节点去留:若当前节点值等于目标值,则跳过当前节点,直接返回处理后的后续链表头;否则保留当前节点作为头节点返回。
代码实现(递归):
class Solution {
public ListNode removeElements(ListNode currentNode, int targetVal) {
if (currentNode == null) {
return null;
}
ListNode processedNext = removeElements(currentNode.next, targetVal);
currentNode.next = processedNext;
if (currentNode.val == targetVal) {
return processedNext;
} else {
return currentNode;
}
}
}-
时间复杂度:O(n)
-
空间复杂度:O(n)
2. 设计链表
题目链接:707. 设计链表 - 力扣(LeetCode)
题目描述:
使用单链表或者双链表,设计并实现自己的链表。
单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。
如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。
实现 MyLinkedList 类:
- MyLinkedList() 初始化 MyLinkedList 对象。
- int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效,则返回 -1 。
- void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后,新节点会成为链表的第一个节点。
- void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。 void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度,那么该节点会被追加到链表的末尾。如果 index 比长度更大,该节点将 不会插入 到链表中。
- void deleteAtIndex(int index) 如果下标有效,则删除链表中下标为 index 的节点。
示例:
输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"]
[[], [1], [3], [1, 2], [1], [1], [1]]
输出
[null, null, null, null, 2, null, 3]
解释
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addAtHead(1);
myLinkedList.addAtTail(3);
myLinkedList.addAtIndex(1, 2); // 链表变为 1->2->3
myLinkedList.get(1); // 返回 2
myLinkedList.deleteAtIndex(1); // 现在,链表变为 1->3
myLinkedList.get(1); // 返回 3
思路提示:
为了简化边界条件的处理,我们可以引入两个哨兵节点: headSentinel:位于链表头部的虚拟节点,其 value 设为 -1。 tailSentinel:位于链表尾部的虚拟节点,其 value 也设为 -1。
初始化时直接相互连接,形成空链表的初始状态(headSentinel.next 指向尾哨兵,tailSentinel.previous 指向头哨兵)
利用元素计数器 elementCount 实时维护链表长度,判断索引有效性。
利用 locateNode 找到指定位置的节点。
-
如果 position < 0 或 >= elementCount,返回 null。
-
如果 position < elementCount / 2,从头部哨兵节点 headSentinel.next 开始,向前遍历。
-
否则,从尾部哨兵节点 tailSentinel.previous 开始,向后遍历。
代码实现(双向链表):
class CustomLinkedList {
private static class DListNode {
DListNode previous, next;
int value;
DListNode(int value) {
this.value = value;
}
}
private final DListNode headSentinel = new DListNode(-1);
private final DListNode tailSentinel = new DListNode(-1);
private int elementCount = 0;
public CustomLinkedList() {
// 初始化双哨兵节点连接
headSentinel.next = tailSentinel;
tailSentinel.previous = headSentinel;
}
public int fetch(int position) {
DListNode target = locateNode(position);
return target != null ? target.value : -1;
}
public void insertFront(int value) {
DListNode newNode = new DListNode(value);
// 建立新节点与后继节点的连接
newNode.next = headSentinel.next;
headSentinel.next.previous = newNode;
// 建立新节点与前驱节点的连接
headSentinel.next = newNode;
newNode.previous = headSentinel;
elementCount++;
}
public void appendEnd(int value) {
DListNode newNode = new DListNode(value);
// 连接新节点到链表尾部
newNode.previous = tailSentinel.previous;
tailSentinel.previous.next = newNode;
newNode.next = tailSentinel;
tailSentinel.previous = newNode;
elementCount++;
}
public void insertAt(int position, int value) {
if (position > elementCount) return;
if (position <= 0) {
insertFront(value);
} else if (position == elementCount) {
appendEnd(value);
} else {
DListNode current = locateNode(position);
DListNode newNode = new DListNode(value);
// 插入新节点到当前节点之前
newNode.previous = current.previous;
newNode.next = current;
current.previous.next = newNode;
current.previous = newNode;
elementCount++;
}
}
public void removeAt(int position) {
DListNode current = locateNode(position);
if (current == null) return;
// 解除当前节点连接
current.previous.next = current.next;
current.next.previous = current.previous;
elementCount--;
}
private DListNode locateNode(int position) {
if (position < 0 || position >= elementCount) return null;
boolean fromHead = position < (elementCount / 2);
int steps = fromHead ? position : elementCount - position - 1;
DListNode current = fromHead ? headSentinel.next : tailSentinel.previous;
while (steps-- > 0) {
current = fromHead ? current.next : current.previous;
}
return current;
}
}3. 反转链表
题目链接:206. 反转链表 - 力扣(LeetCode)
题目描述:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
思路提示:
依旧可以使用迭代和递归两种方法。
- 迭代:通过迭代的方式,在遍历链表的过程中,逐步改变每个节点的指针方向,让原本指向下一个节点的指针改为指向前一个节点,最终实现链表的反转。
- 递归:通过递归逐步调整每个节点的指针方向,使其指向前一个节点。递归终止条件是链表为空或只有一个节点,此时无需反转。在递归返回时,将当前节点的下一个节点的
next指针指向当前节点,并将当前节点的next指针设置为null,以避免环的出现。最终返回反转后的链表头节点,即递归调用的返回值。
代码实现:
迭代
class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}
class Solution {
public ListNode reverseList(ListNode startNode) {
ListNode previous = null;
ListNode current = startNode;
while (current != null) {
ListNode nextNode = current.next;
current.next = previous;
previous = current;
current = nextNode;
}
return previous;
}
}-
时间复杂度:O(n)
-
空间复杂度:O(1)
递归
class ListNode {
int value;
ListNode nextNode;
ListNode(int num) {
value = num;
}
}
class ReverseSolution {
// 递归反转链表的方法
public ListNode reverseList(ListNode head) {
// 若链表为空或者只有一个节点,直接返回该节点
if (head == null || head.nextNode == null) {
return head;
}
// 递归调用反转后续节点
ListNode newHead = reverseList(head.nextNode);
// 反转当前节点和下一个节点的指向关系
head.nextNode.nextNode = head;
// 断开当前节点原来的指向
head.nextNode = null;
// 返回新的头节点
return newHead;
}
}-
时间复杂度:O(n)
-
空间复杂度:O(n)
4. 两两交换链表中的节点
题目链接:24. 两两交换链表中的节点 - 力扣(LeetCode)
题目描述:
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。
示例:
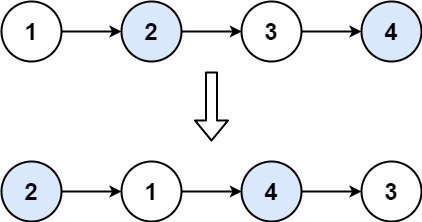
输入:head = [1,2,3,4]
输出:[2,1,4,3]
思路提示:
依旧可以使用迭代和递归两种方法。
- 迭代:首先创建虚拟头节点
fakeHead并让current指向它,以此简化头节点处理。接着用while循环遍历链表,只要当前节点后至少有俩节点,就定义firstNode和secondNode并交换位置。每次交换后,current移到firstNode处处理下一组。最后返回fakeHead.next即交换后链表头。 - 递归:先判断链表是否为空。若链表为空或仅一个节点则直接返回。若有两个及以上节点,把第二个节点设为新头节点,接着递归交换后续节点,将原头节点连到交换后节点链,再把新头节点指向原头节点,最后返回新头节点。
代码实现:
迭代
class ListNode {
int val;
ListNode next;
ListNode(int value) {
val = value;
}
}
class PairSwapper {
public ListNode swapNodePairs(ListNode listHead) {
// 创建虚拟头节点
ListNode fakeHead = new ListNode(0);
fakeHead.next = listHead;
ListNode current = fakeHead;
// 只要当前节点之后至少还有两个节点就继续循环
while (current.next != null && current.next.next != null) {
ListNode firstNode = current.next;
ListNode secondNode = current.next.next;
// 交换节点
current.next = secondNode;
firstNode.next = secondNode.next;
secondNode.next = firstNode;
// 移动当前节点到下一组待交换节点的前一个位置
current = firstNode;
}
return fakeHead.next;
}
}-
时间复杂度:O(n)
-
空间复杂度:O(1)
递归
class Node {
int value;
Node nextNode;
Node(int num) {
value = num;
}
}
class SwapSolution {
public Node swapNodePairs(Node listHead) {
if (listHead == null || listHead.nextNode == null) {
return listHead;
}
Node newListHead = listHead.nextNode;
listHead.nextNode = swapNodePairs(newListHead.nextNode);
newListHead.nextNode = listHead;
return newListHead;
}
}-
时间复杂度:O(n)
-
空间复杂度:O(n)
5. 删除链表倒数第n个结点
题目链接:19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
题目描述:
给你一个链表,删除链表的倒数第 n 个结点,并返回链表的头结点。
示例:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
思路提示:
非常经典的双指针(快慢指针)问题。先创建虚拟头节点 fakeHead,让快慢指针都指向它。快指针先移动 n 步,之后快慢指针同步移动,直到快指针到链表末尾。此时慢指针的下一个节点就是要移除的节点,调整慢指针的 next 指向跳过该节点,最后返回 fakeHead.next。
代码实现:
class ListNode {
int val;
ListNode next;
ListNode(int value) {
val = value;
}
}
class NodeRemover {
public ListNode removeNthNodeFromEnd(ListNode listHead, int n) {
ListNode fakeHead = new ListNode(0);
fakeHead.next = listHead;
ListNode slowPtr = fakeHead;
ListNode fastPtr = fakeHead;
if (listHead == null || listHead.next == null) {
return null;
}
for (int i = 0; i < n; i++) {
fastPtr = fastPtr.next;
}
while (fastPtr.next != null) {
slowPtr = slowPtr.next;
fastPtr = fastPtr.next;
}
slowPtr.next = slowPtr.next.next;
return fakeHead.next;
}
}-
时间复杂度:O(L),其中 L 是链表的长度。
-
空间复杂度:O(1)
6. 相交链表
题目链接:160. 相交链表 - 力扣(LeetCode)
题目描述:
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
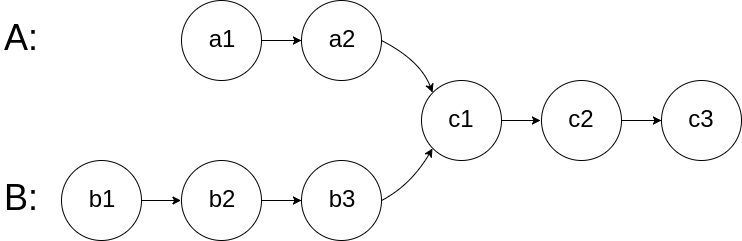
函数返回结果后,链表必须 保持其原始结构 。
示例1:
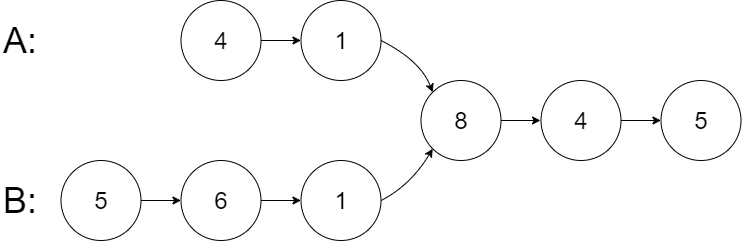
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。 — 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例2:
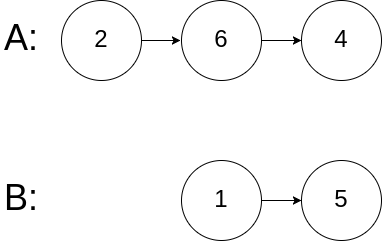
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:No intersection
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
思路提示:
又是一道经典的双指针(快慢指针)问题。具体实现方式如下:
- 初始化指针: 定义两个指针 pointer1 和 pointer2,分别指向链表 listA 和 listB 的头节点。
- 双指针同步遍历: 使用 while 循环来不断移动指针,循环条件是 pointer1 != pointer2。也就是说,只要两个指针没有相遇,就会继续循环。
- 在每次循环中,对指针进行如下操作:若
pointer1为空,表明它已经遍历完链表listA,此时将其指向链表listB的头节点;否则,将pointer1移动到下一个节点。若pointer2为空,表明它已经遍历完链表listB,此时将其指向链表listA的头节点;否则,将pointer2移动到下一个节点。 - 返回结果: 当 pointer1 和 pointer2 相遇时,循环结束。此时 pointer1 所指向的节点就是两个链表的相交节点;若两个链表不相交,那么 pointer1 和 pointer2 最终都会指向 null,因此返回 null。
代码实现:
public class IntersectionLocator {
public ListNode findIntersectionNode(ListNode listA, ListNode listB) {
ListNode pointer1 = listA, pointer2 = listB;
// 双指针同步遍历机制
while (pointer1 != pointer2) {
// 指针1到达末尾后转接链表B
pointer1 = (pointer1 == null) ? listB : pointer1.next;
// 指针2到达末尾后转接链表A
pointer2 = (pointer2 == null) ? listA : pointer2.next;
}
return pointer1; // 返回相遇节点或null
}
}-
时间复杂度:O(m + n),其中 m 和 n 分别是链表
listA和listB的长度。 -
空间复杂度:O(1)
7. 环形链表
题目链接:141. 环形链表 - 力扣(LeetCode)
题目描述:
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例:
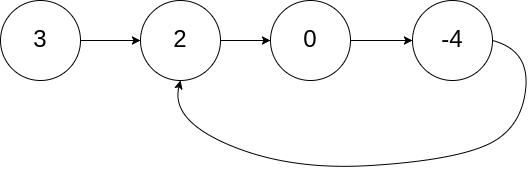
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
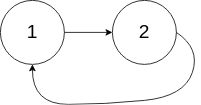
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
思路提示:
依旧可以使用快慢指针的方法。
首先检查链表是否为空或只有一个节点,若满足则无环。接着初始化慢指针指向头节点,快指针指向头节点的下一个节点。循环中,快指针若到链表末尾则无环;若未到末尾,慢指针走一步,快指针走两步。若快慢指针相遇则链表有环。
代码实现:
public class CycleDetector {
public boolean checkForCycle(ListNode startNode) {
// 处理空链表或单节点无环情况
if (startNode == null || startNode.next == null) {
return false;
}
ListNode tortoise = startNode; // 慢指针
ListNode hare = startNode.next; // 快指针
// 双指针追逐检测
while (tortoise != hare) {
// 快指针提前到达终点
if (hare == null || hare.next == null) {
return false;
}
tortoise = tortoise.next; // 慢指针前进1步
hare = hare.next.next; // 快指针前进2步
}
return true; // 相遇即存在环
}
}-
时间复杂度:O(n)
-
空间复杂度:O(1)
8. 环形链表 Ⅱ
题目链接:142. 环形链表 II - 力扣(LeetCode)
题目描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
示例:

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
思路提示:
第一阶段:检测环的存在
- 指针初始化:初始化两个指针
hare(快指针)和tortoise(慢指针),都指向链表的起始节点startNode。 - 指针移动与环检测:使用
do-while循环来移动指针。在每次循环中,快指针hare每次移动两步(hare = hare.next.next),慢指针tortoise每次移动一步(tortoise = tortoise.next)。 - 无环判断:在移动指针的过程中,会检查快指针
hare是否已经到达链表末尾(hare == null)或者快指针的下一个节点是否为null(hare.next == null)。如果满足这些条件,说明链表中不存在环,直接返回null。 - 环存在判断:如果快指针
hare和慢指针tortoise相遇了,说明链表中存在环,此时第一阶段结束,进入第二阶段。
第二阶段:定位环入口
- 重置快指针:将快指针
hare重新指向链表的起始节点startNode。 - 同步移动指针:此时快指针
hare和慢指针tortoise每次都移动一步(hare = hare.next和tortoise = tortoise.next),直到它们再次相遇。 - 确定环入口:当快指针
hare和慢指针tortoise再次相遇时,相遇的节点就是链表中环形部分的起始节点,将该节点返回。
数学原理
设链表头节点到环入口的距离为 a,环入口到快慢指针相遇点的距离为 b,相遇点再到环入口的距离为 c。当快慢指针相遇时,慢指针走过的距离为 a + b,快指针走过的距离为 a + b + k * (b + c)(k 为快指针在环内绕的圈数,k >= 1)。由于快指针速度是慢指针的两倍,所以有 2 * (a + b) = a + b + k * (b + c),化简可得 a = (k - 1) * (b + c) + c。这意味着从链表头节点和快慢指针相遇点同时出发,以相同的速度移动,最终会在环入口处相遇。
代码实现:
public class CycleEntranceFinder {
public ListNode findCycleStart(ListNode startNode) {
ListNode hare = startNode, tortoise = startNode;
// 第一阶段:检测环是否存在
do {
// 快指针无法继续前进则无环
if (hare == null || hare.next == null) return null;
hare = hare.next.next;
tortoise = tortoise.next;
} while (hare != tortoise);
// 第二阶段:定位环入口
hare = startNode; // 重置快指针到起点
while (hare != tortoise) {
hare = hare.next;
tortoise = tortoise.next;
}
return hare;
}
}-
时间复杂度:O(n)
-
空间复杂度:O(1)
总结
在面试及算法学习中,链表作为重要的数据结构类型,是考察的重点内容。链表问题虽在结构理解上有一定复杂度,但通过掌握经典算法思想与解题技巧,能够高效应对各类题目。以下是链表经典题型及其核心思想的总结:
1. 虚拟头节点简化边界处理
核心思想:引入虚拟头节点,将头节点删除等特殊情况转化为普通节点处理,统一操作逻辑,降低代码实现难度。
关键点:
虚拟节点的创建与初始化,使其next指针指向原链表头节点。
遍历或定位节点时,从虚拟头节点开始操作,最终返回虚拟头节点.next作为新链表头。
2. 迭代和递归思想
核心思想:大部分链表题目都可以通过迭代和递归两种方式解决。
- 迭代:通过循环结构,按顺序依次处理链表节点,更新指针指向。
- 递归:将问题分解为规模更小的子问题,利用函数自身调用,从链表尾部或子结构开始处理,再回溯调整指针。
关键点:
- 迭代:明确循环终止条件,合理保存和更新节点指针。
- 递归:确定递归终止条件,处理好函数返回值与节点指针的关联。
3. 双指针(快慢指针应用)
题目:19. 删除链表的倒数第 N 个结点、160. 相交链表、141. 环形链表、142. 环形链表 Ⅱ
核心思想:利用两个速度不同的指针,通过相对位置关系解决节点定位、环检测与环入口查找等问题,将时间复杂度优化至线性或更优。
关键点:根据不同问题,利用快慢指针相遇或特定位置关系得出结论,如环形链表 Ⅱ 中通过数学推导确定环入口。
链表相关题目通过多种经典算法思想与技巧的结合,考查对数据结构特性的理解与灵活运用能力。掌握这些核心思想,不仅有助于解决链表问题,更能迁移到树、图等复杂数据结构的学习中。在面试与日常学习中,需通过大量练习强化对链表操作的熟练度,提升算法设计与代码实现能力。
下期将探讨另一个重要算法结构——哈希表,会结合Java代码进行讲解,希望能帮大家更好地掌握算法结构。
谢谢大家的支持~




















 1614
1614

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








