算法学习——数组（刷题训练及总结）

初始化指针：设定两个指针 slow 和 fast，其中 slow 指向数组的第一个元素（nums[0]），而 fast 则指向 slow 的下一个位置（nums[1]）。
遍历数组：快指针不断向后移动，并将其所指向的元素与慢指针所指向的元素进行比较：
- 若 nums[fast] 与 nums[slow] 不相等，这意味着我们找到了一个新的不重复元素。此时，我们将 nums[fast] 的值赋给 nums[slow + 1]，然后 slow 指针前移一位，以准备接收下一个可能的不重复元素。
- 若 nums[fast] 与 nums[slow] 相等，则表明当前元素是重复的，fast 指针继续后移，寻找下一个不重复的元素。
终止条件：当 fast 指针遍历完整个数组后，slow 指针所指向的位置即为去重后数组的最后一个元素的位置。因此，去重后的数组长度为 slow + 1。

通过这种方式，慢指针slow始终指向当前已处理的不重复子数组的最后一个元素，而快指针fast负责遍历整个数组，查找新的不同元素并将其插入到慢指针的下一个位置。最终，当快指针遍历完整个数组时，慢指针slow的位置加1即为删除重复元素后的数组长度。

代码实现：

class Solution {
    public int removeDuplicates(int[] nums) {
        if(nums.length == 0){return 0;}
        int slow = 0, fast = 1;
        while(fast < nums.length){
            if(nums[fast] != nums[slow]){
                slow = slow + 1;
                nums[slow] = nums[fast];
            }
            fast = fast + 1;
        }
        return slow + 1;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

283. 删除有序数组中的重复项

题目链接：283. 移动零 - 力扣（LeetCode）

题目描述：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入：nums = [0,1,0,3,12]

输出：[1,3,12,0,0]

示例 2:

输入：nums = [0]

输出：[0]

思路提示：

采用双指针法来处理数组，其中 left 指针指向当前已处理部分的尾部，而 right 指针指向待处理部分的起始位置。使用 right 指针遍历数组中的每一个元素。当 right 指针指向的元素为非零值时，将其与 left 指针指向的元素进行交换，随后将 left 指针右移一位。

这种操作基于以下特性：

left 指针左侧元素均为非零值，且保持了原始顺序；
left 指针与right 指针之间的区域均为零。

因此，每次交换操作都将一个零值（位于 left 指针处）与一个非零值（位于 right 指针处）互换，同时保证了非零元素的相对顺序保持不变。通过这种方式，零值被逐步移动到数组的末尾，而非零值的相对顺序保持不变。

当 right 指针遍历完整个数组后，所有非零值均已移动到数组的前部，而零值则被集中到数组的尾部。

代码实现：

class Solution {
    public void moveZeroes(int[] nums) {
        int n = nums.length;
        int left = 0, right = 0;

        while (right < n) {
            if (nums[right] != 0) {
                swap(nums, left, right);
                left++;
            }
            right++;
        }
    }

    public void swap(int[] nums, int left, int right) {
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

27. 移除元素

题目链接：27. 移除元素 - 力扣（LeetCode）

题目描述：

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。

示例 1:

输入：nums = [3,2,2,3], val = 3

输出：2, nums = [2,2,_,_]

解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2:

输入：nums = [0,1,2,2,3,0,4,2], val = 2

输出：5, nums = [0,1,4,0,3,_,_,_]

解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。注意这五个元素可以任意顺序返回。你在返回的 k 个元素之外留下了什么并不重要（因此并不计入评测）。

思路提示：

题目要求原地删除数组中所有等于 val 的元素，并返回新数组的长度。由于新数组的长度一定小于或等于原数组的长度，我们可以利用双指针直接在原数组上进行操作。left 指针指向下一个待赋值的位置，right 指针用于遍历数组中的每一个元素

如果 nums[right] 不等于val，说明该元素需要保留，因此将其赋值给 nums[left]，并将 left 和 right 指针同时右移。
如果 nums[right] 等于val，则该元素需要被删除，因此仅将right指针向右移动一位，而left指针保持不动。

整个过程中，始终保证[0, left)区间内的元素都不等于val（即该区间内的元素为最终输出的有效元素）。当right指针遍历完整个数组后，left指针的值即为新数组长度。

代码实现：

class Solution {
    public int removeelement(int[] nums, int val) {
        int left = 0;
        for (int right = 0; right < nums.length; right++) {
            if (nums[right] != val) {
                nums[left] = nums[right];
                left++;
            }
        }
        return left;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

485. 最大连续1的个数

题目链接：485. 最大连续 1 的个数 - 力扣（LeetCode）

题目描述：

给定一个二进制数组 nums ，计算其中最大连续 1 的个数。

示例 1:

输入：nums = [1,1,0,1,1,1]

输出：3

解释：开头的两位和最后的三位都是连续 1 ，所以最大连续 1 的个数是 3.

示例 2:

输入：nums = [1,0,1,1,0,1]

输出：2

思路提示：

在处理数组nums时，我们可以通过遍历数组并动态维护两个变量：一个是当前连续1的计数（currentCount），另一个是迄今为止遇到的最大连续1的计数（maxCount）。初始时，这两个变量都设为0。在遍历数组时：

如果当前元素是1，则将 currentCount 加 1。
如果当前元素是0，说明连续1的序列被中断，此时需要将currentCount与maxCount进行比较，并用较大的值更新maxCount，然后将currentCount重置为0。

遍历结束后，还需要再次检查currentCount，因为数组的最后一个元素可能是1，且最长连续 1 的子数组可能正好位于数组的末尾。如果不进行这一步更新，可能会导致最终结果错误。

代码实现：

class Solution {
    public int findMaxConsecutiveOnes(int[] nums) {
        int maxCount = 0, currentCount = 0;
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                currentCount++;
            } else {
                maxCount = Math.max(maxCount, currentCount);
                count = 0;
            }
        }
        maxCount = Math.max(maxCount, currentCount);
        return maxCount;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

704. 二分查找

题目链接：704. 二分查找 - 力扣（LeetCode）

题目描述：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入：nums = [-1,0,3,5,9,12], target = 9

输出：4

解释：9 出现在 nums 中并且下标为 4

示例 2:

输入：nums = [3,2,4], target = 6

输出：-1

解释：6 不存在于nums 中，因此返回 -1

思路提示：

在升序数组 nums 中找目标值 target，可以利用数组的有序性，通过二分查找高效地定位目标值。

二分查找的思路如下：

定义一个搜索区间[left, right]，初始时为整个数组。
每次计算区间的中点mid，并比较nums[mid]与target：
- 若nums[mid]等于target，则找到目标值，返回下标mid；
- 若nums[mid]大于target，则目标值位于 mid 左侧，缩小查找范围为 [left, mid-1]。
- 若nums[mid]小于target，则目标值位于 mid 右侧，缩小查找范围为 [mid+1, right]。
重复上述过程，直到搜索区间为空（即left > right）。

关键性质：

每次查找都将查找范围缩小一半，因此算法的时间复杂度为 O(log n)，其中 n 为数组长度。
二分查找的前提是数组必须有序。

代码实现：

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) {
                right = mid - 1; 
            } else {
                left = mid + 1;
            }
        }

        return -1; // 未找到目标值，返回 -1
    }
}

时间复杂度：O(logn)
空间复杂度：O(1)

209. 长度最小的子数组

题目链接：209. 长度最小的子数组 - 力扣（LeetCode）

题目描述：

示例 1:

输入：target = 7, nums = [2,3,1,2,4,3]

输出：2

解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2:

输入：target = 4, nums = [1,4,4]

输出：1

示例 3:

输入：target = 11, nums = [1,1,1,1,1,1,1,1]

输出：0

思路提示：

为了找到满足条件的最短子数组，我们可以使用滑动窗口的方法。滑动窗口由两个指针start和end定义，分别表示子数组的起始位置和结束位置。同时，我们用一个变量sum来记录当前子数组中所有元素的和，变量minLen用于记录满足条件的最短子数组长度。

初始时，start和end都指向数组的第一个元素（下标0），sum初始化为0。
使用 end 指针遍历数组中的每一个元素，在每一轮迭代中，首先将nums[end]加入到sum中。当sum大于或等于目标值s时，表示当前子数组满足条件。此时，我们计算子数组的长度（end-start+1），并更新已知的最短长度。
接下来，从sum中减去nums[start]，并将start右移来缩小窗口，直到sum小于s。
无论sum是否满足条件，都将end右移一位，继续探索下一个可能的子数组。

通过这种方式，start和end指针不断移动，滑动窗口也随之扩展或收缩，从而在遍历数组的过程中找到满足条件的最短子数组。

代码实现：

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int start = 0;
        int sum = 0; 
        int minLen = Integer.MAX_VALUE; 
        if (n == 0) {
            return 0;
        }
        for (int end = 0; end < nums.length; end++) {
            sum += nums[end];
            while (sum >= s) {
                minLen = Math.min(minLen, end - start + 1);
                sum -= nums[start];
                start++; 
            }
        }
        // 如果 minLen 未被更新，说明不存在满足条件的子数组
        return minLen == Integer.MAX_VALUE ? 0 : minLen;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

59. 螺旋矩阵 II

题目链接：59. 螺旋矩阵 II - 力扣（LeetCode）

题目描述：

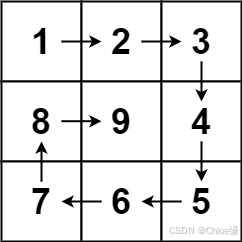
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1:

输入：n = 3

输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2:

输入：n = 1

输出：[[1]]

思路提示：

为了生成一个 n x n 的螺旋矩阵，我们可以通过模拟填充过程来实现。具体步骤如下：

创建一个 n x n 的二维数组 matrix，并将其所有元素初始化为 0。定义四个方向：向右、向下、向左、向上。使用一个方向数组 directions 表示这四个方向的移动增量。
定义变量 row 和 col表示当前填充位置的行和列，初始值为 0；currentDirection表示当前移动方向，初始值为向右；num表示当前填充的数字，初始值为 1。
从 1 到 n x n，依次填充矩阵：
- 更新当前位置为下一个位置，并递增 num。
- 如果下一个位置超出矩阵边界，或者已经被填充过（即 matrix[nextRow][nextCol] != 0），则顺时针旋转方向，更新 currentDirection。
- 计算下一个位置的行和列：nextRow = row + directions[currentDirection][0]，nextCol = col + directions[currentDirection][1]。
- 将当前数字 num 填入 matrix[row][col]。
当 num 达到 n * n 时，矩阵填充完成。

代码实现：

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n]; // 初始化矩阵
        int[][] directions = {
  {0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 方向数组：右、下、左、上
        int currentDirection = 0; // 当前方向，初始为向右
        int row = 0, col = 0; // 当前位置
        int num = 1; // 当前填充的数字

        // 填充矩阵
        while (num <= n * n) {
            matrix[row][col] = num++; // 填充当前数字

            // 计算下一个位置
            int nextRow = row + directions[currentDirection][0];
            int nextCol = col + directions[currentDirection][1];

            // 如果下一个位置超出边界或已被填充，则改变方向
            if (nextRow < 0 || nextRow >= n || nextCol < 0 || nextCol >= n || matrix[nextRow][nextCol] != 0) {
                currentDirection = (currentDirection + 1) % 4; // 顺时针旋转方向
                nextRow = row + directions[currentDirection][0];
                nextCol = col + directions[currentDirection][1];
            }

            // 更新当前位置
            row = nextRow;
            col = nextCol;
        }

        return matrix;
    }
}