算法竞赛——01基础数据结构

1.1 链表

  链表的特点是用一组位于“任意位置”的存储单元存储线性表的数据元素，这组存储单元可以是“连续的，也可以不连续”。链表是容易理解和操作的基本数据结构，它的操作有初始化、添加、遍历、插入、删除、查找、释放等。链表分为单向链表和双向链表，如下图所示。

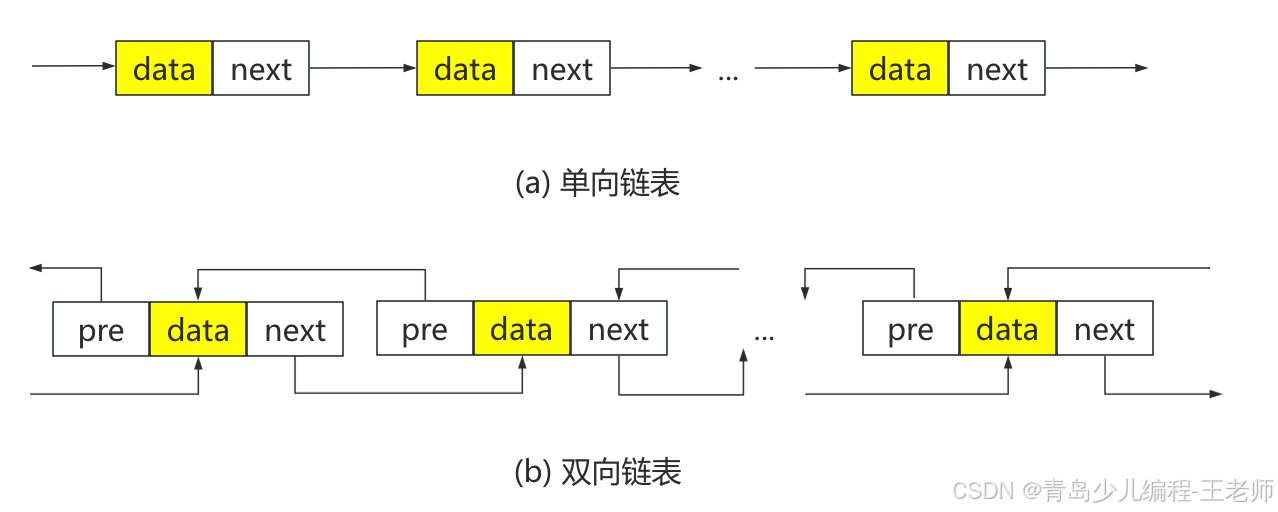
  链表一般是循环的，首尾相接，最后一个节点的next指针指向第$1$个节点，第$1$个节点的pre指针指向最后一个节点。单向链表只有“一个”遍历方向，双向链表有“两个”遍历方向，比单项链表的访问方便一些，也快一些。在需要“频繁访问”前后几个节点的场合可以使用双向链表。
  使用链表时，可以直接使用STL list，也可以自己写链表。如果自己写代码实现链表，有两种编码实现方法：“动态链表”，“静态链表”。在算法竞赛中为加快编码速度，一般用“静态链表”或“STL list”。

例1.1  P1996 约瑟夫问题

  以下分别给出动态链表、静态链表、STL链表等$3$种方案、$5$种代码来解决“例1.1 P1996 约瑟夫问题”。这$5$种代码的“逻辑和流程完全一样”，只有链表的实现不一样。

1.1.1-动态链表

  动态链表需要临时分配链表节点，使用完毕后释放链表节点。动态链表的优点是能及时释放空间，不使用多余内存；缺点是徐亚松管理空间，容易出错。动态链表时教科书式的标准做法

// 例1.1 P1996 约瑟夫问题 动态链表
#include <iostream>

using namespace std;

struct node{
   
   	// 定义链表节点
	int data;	// 节点的值
	node *next;	//单向链表，只有一个next指针
};

int main(){
   
   
	int n, m;
	cin >> n >> m;
	node *head, *p, *now, *prev;  // p指针用于新建节点， now和prev指针用于遍历和修改
	head = new node;
	head->data = 1;
	head->next = NULL; // 分配第一个节点

	now = head; // 当前指向的指针 
	for (int i = 2; i <= n; i++){
   
   
		p = new node;
		p->data = i;
		p->next = NULL; // p是一个新节点
		now->next = p; // 把申请的新节点连到前面的链表上
		now = p; // 尾指针后移一个
	}	
	now->next = head; // 尾指针指向头：循环链表建立完成
// 以上是建立链表，下面是本题的逻辑和流程
	now = head;
	prev = head; 
	while ((n--) > 1){
   
   
		for (int i = 1; i < m; i++){
   
    // 数到m停下
			prev = now; // 记录上一个位置，用于下面跳过第m个节点
			now = now->next;
		}
		cout << now->data << ' '; //输出第m个节点，带空格
		prev->next = now->next; //跳过这个节点
		delete now; // 释放节点
		now = prev->next; // 新的一轮
	}
	cout << now->data; // 输出最后一个节点
	delete now;  // 释放最后一个节点
	return 0;
}

动态链表虽然标准，但是“竞赛中一般不用”，竞赛算法对内存管理要求不严格，为加快编码速度，一般就在题目允许的存储空间内静态分配，省去了动态分配和释放的麻烦。

1.1.2-静态链表

  静态链表使用预先分配的一段连续空间存储链表。从物理存储的意义上讲，"连续空间"并不符合链表的本义，因为链表的优点就是能克服连续存储的弊端。但是，用连续空间实现的链表，在逻辑上是成立的。具体有两种做法：
$（1）$定义链表结构体数组，和动态链表的结构差不多
$（2）$使用一味数组，直接在数组上进行链表操作

1. 用结构体数组实现单向静态链表

// 例1.1 P1996 约瑟夫问题 用结构体数组实现单向静态链表
#include <iostream>

using namespace std;
const int N = 105;
struct node{
   
    // 单向链表
	int id, nextid; // 单向指针
	// int data; // 如果有必要，定义一个有意义的数据
}nodes[N];

int main(){
   
   
	int n, m;
	cin >> n >> m;
	nodes[0].nextid = 1;
	for (int i = 1; i <= n; i++){
   
   
		nodes[i].id = i;
		nodes[i].nextid = i + 1;
	}	
	nodes[n].nextid = 1;   // 循环链表，尾指向头
	int now = 1, prev = 1; // 从第一个节点开始
	while ((n--) > 1){
   
   
		for (int i = 1; i < m; i++){
   
    //数到m停下
			prev = now;
			now = nodes[now].nextid;
		}
		cout << nodes[now].id << ' ';
		nodes[prev].nextid = nodes[now].nextid; // 跳过now节点，即删除now
		now = nodes[prev].nextid;
	}
	cout << nodes[now].nextid << endl;
	return 0;
}

2. 用结构体数组实现双向静态链表

// 例1.1 P1996 约瑟夫问题 用结构体数组实现双向静态链表
#include <iostream>

using namespace std;
const int N = 105;
struct node{
   
    // 双向链表
	int id; // 节点编号
	// int data; // 如果有必要，定义一个有意义的数据
	int preid, nextid; // 前一个节点，后一个节点
}nodes[N];

int main(){
   
   
	int n, m;
	cin >> n >> m;
	nodes[0].nextid = 1;
	for (int i = 1; i <= n; i++){
   
    // 建立链表
		nodes[i].id = i;	
		nodes[i].preid = i - 1;	// 前节点
		nodes[i].nextid = i + 1; // 后节点
	}	
	nodes[n].nextid = 1;   // 循环链表，尾指向头
	nodes[1].preid = n;    // 循环链表，头指向尾
	int now = 1; // 从第一个节点开始
	while ((n--) > 1){
   
   
		for (int i = 1; i < m; i++){
   
    //数到m停下
			now = nodes[now].nextid;
		}
		cout << nodes[now].id << ' ';
		int prev = nodes[now].preid, next = nodes[now].nextid;
		nodes[prev].nextid = nodes[now].nextid; // 删除now
		nodes[next].preid = nodes[now].preid;
		now = next;
	}
	cout << nodes[now].nextid << endl;
	return 0;
}

3. 用一维数组实现单向静态链表：这是最简单的实现方法。定义一个一维数组nodes[], nodes[i]的i就是节点的值，而nodes[i]的值时下一个节点。它的使用环境很有限，因为它的节点只能存一个数据，就是i。

// 例1.1 P1996 约瑟夫问题 用一维数组实现单向静态链表
#include <iostream>

using namespace std;
const int N = 105;
int nodes[N];

int main(){
   
   
	int n, m;
	cin >> n >> m;
	for (int i = 1; i < n; i++){
   
   
		nodes[i] = i + 1; // nodes[i]的值就是下一个节点
	}
	nodes[n] = 1; // 循环链表：尾指向头
	int now = 1, prev = 1;
	while ((n--) > 1){
   
   
		for (int i = 1; i < m; i++){
   
   
			prev = now;
			now = nodes[now];
		}
		cout << now << ' ';
		nodes[prev] = nodes[now];
		now = nodes[prev]; 
	}
	cout << now << endl;
	return 0;
}

1.1.3-STL list

  在算法竞赛或工程项目中常常使用C++ STL list。list是双向链表，由标准模版库（Standard Template Library， STL）管理，通过指针访问节点数据，高效率地删除和插入。

// 例1.1 P1996 约瑟夫问题 STL list
#include <iostream>
#include <list>
using namespace std;

int main(){
   
   
	int n, m;
	cin >> n >> m;
	list<int> node;
	for (int i = 1; i <= n; i++){
   
   
		node.push_back(i); // 建立链表
	}
	list<int>::iterator it = node.begin();
	while (node.size() > 1){
   
   
		for (int i = 1; i < m; i++){
   
   
			it++;
			if(it == node.end()) {
   
   
				it = node.begin(); // 循环：到末尾后再回头
			}
		}
		cout << *it << ' ';
		list<int>::iterator next = ++it;
		if (next == node.end()){
   
   
			next = node.begin(); // 循环链表
		}
		node.erase(--it); // 删除这个节点，node.size()自动减1
		it = next;
	}
	cout << *it;
	return 0;
}

1.1.4-链表相关练习题

序号	链接	难度
1	B3631 单向链表	普及-
2	P1160 队列安排	普及/提高-

1.2 队列

  队列中的数据存取方式是先进先出，只能向队尾插入元素，从队头移出数据。队列的原型在生活中很常见，如食堂打饭的队伍，先到先服务。队列有两种实现方式：链队列，循环队列，如下图所示。

  链队列可以看作单链表的一种特殊情况，用指针把各个节点连接起来。
  循环队列是一种顺序表，使用一组连续的存储单元依次存放队列元素，用两个指针head和tail分别指示队头元素和队尾元素，当head和tail走到底时，下一步回到开始的位置，从而在这组连续空间内循环。循环队列能解决溢出问题。如果不循环，head和tail都一致往前走，可能会走到存储空间之外，导致溢出。
  队列和栈的主要问题是查找较慢，需要从头到尾一个个查找。在某些情况下可以用优先队列，让优先级最高（最大的数或最小的数）先出队列。
  队列的代码很容易实现，如果使用环境简单，最简单的手写队列代码如下：

const int N = 1e5;
int que[N], head, tail; // 队头队尾指针，队列大小为tail - head + 1
head++; 	// 弹出队头， 注意  head <= tail
que[head]; 	// 读队头数据
que[++tail] = data; 	//输入data入队，尾指针加1，注意不能溢出
// 这个队列不是循环的，tail可能超过N，导致溢出。

1.2.1-STL queue

  STL queue的主要操作如下：

$(1)$queue<Type>q : 定义队列，Type为数据类型，如int、double、char等。
$(2)$q.push(item): 把item放进队列
$(3)$q.front():返回队首元素，但不会删除。
$(4)$q.pop():删除队首元素。
$(5)$q.back():返回队尾元素。
$(6)$q.size():返回元素个数。
$(7)$q.empty():检查队列是否为空.

例1.2  P1540 [NOIP2010 提高组] 机器翻译

// 例1.2  P1540 [NOIP2010 提高组] 机器翻译 STL queue
#include <iostream>
#include <queue>
using namespace std;
int Hash[1003] = {
   
   0}; // 用哈希检查内存中有没有单词，Hash[i]=1表示单词i在内存中
queue <int> mem; // 用队列模拟内存
int main(){
   
   
	int m, n;
	cin >> m >> n;
	int cnt = 0; // 查字典的次数
	while (n--){
   
   
		int en;
		cin >> en; // 输入一个英文单词
		if(!Hash[en]){
   
    // 如果内存中没有这个单词
			++cnt; 
			mem.push(en);	// 单词入队列，放到队列尾部
			Hash[en] = 1; // 记录内存中有这个单词
			while (mem.size() > m){
   
    // 内存满了
				Hash[mem.front()] = 0; // 从内存中去掉单词
				mem.pop(); // 从队头去掉
			}
		}
	}
	cout << cnt << endl;
	return 0;
}

1.2.2-手写循环队列

  下面是循环队列的手写模版，代码中给出了静态分配空间和动态分配空间两种方式(动态分配实现放在注释中)。竞赛中一般使用静态分配。

// 例1.2  P1540 [NOIP2010 提高组]