动态规划、有限状态机与有向无环图的内在统一性探究

原创已于 2025-11-25 21:11:57 修改 · 959 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #垃圾小作文

于 2025-11-23 19:00:00 首次发布

前言

对于动态规划、有限状态自动机和有向无环图（DAG），这三者之间其实具有非常相似的内核。至少我是这么认为的。接下来，我想做一些简单的感性探讨：

一般来说，动态规划问题可以用递归来解决，这说明这类问题存在最小子问题，也就是说，它们可以被拆解成规模更小的子问题。在解决动态规划问题时，我们通常关注的是状态转移方程，而有限状态自动机正是这种数学表达的执行者。进一步来看，如果我们把它的“行走路径”可视化出来，那它就是一个有向无环图；更具体、更特殊一点，它其实就是一个决策树。

那么，为什么偏偏是有限状态自动机和有向无环图呢？

说它与有限状态自动机内核相同，是因为动态规划的状态转移来源是有限的：有一个起点，以及若干个（但总是可以确定的）可选分支。而有向无环图则是因为整个状态转移过程是不可逆的——我们无法从后续状态反推之前的状态（当然，这个结论可能不一定完全准确）。而且，如果图中存在环，那么自动机就可能会在这个环中“迷路”（一直在这个环上”打转“。因为我们没有对它的路径做限制）。而我们最终想要的状态，一定是图上某个确定的节点。

总而言之，有向无环是为了保证我们最终能得到确定的结果；有限状态自动机则是因为状态来源是有限的。

所以，我们可以这样理解：动态规划是策略，有限状态自动机是执行者，有向无环图是记录者。

在理解这个前提之后，我们就可以开始更具体、更理性的讨论了：

从解决力扣题时总结出的心法切入，引出对更普适计算模型的思考。

本文将通过一个“从生活直觉到理论抽象，再从理论辨析到本质洞察”的独特路径，揭示动态规划（DP）、有限状态机（FSM）与有向无环图（DAG）如何从不同角度描述同一计算过程。

第一章：引入：从基础的DP出发

1.1 起点：实践中的发现

题目很直白，让我们统计爬到顶楼的路径总共有多少。

直接启动逆向思考，总共有n阶，我想要上到第n台阶就有：从n-1阶再走一步，n-2阶再走两步这两部分的办法，而且它们之间相互不重叠。所以直接把它们的方案数相加就能得到上到第n阶的总方案数了。

这样分解问题的方法对上到n-1、n-2级台阶也同样适用。在初始的第零阶（不走，一种方法到达）和第一阶（只走一步，也是一种方法到达）所以：

dp[0]=1
dp[1]=1
dp[i]=dp[i−1]+dp[i−2],i≥2

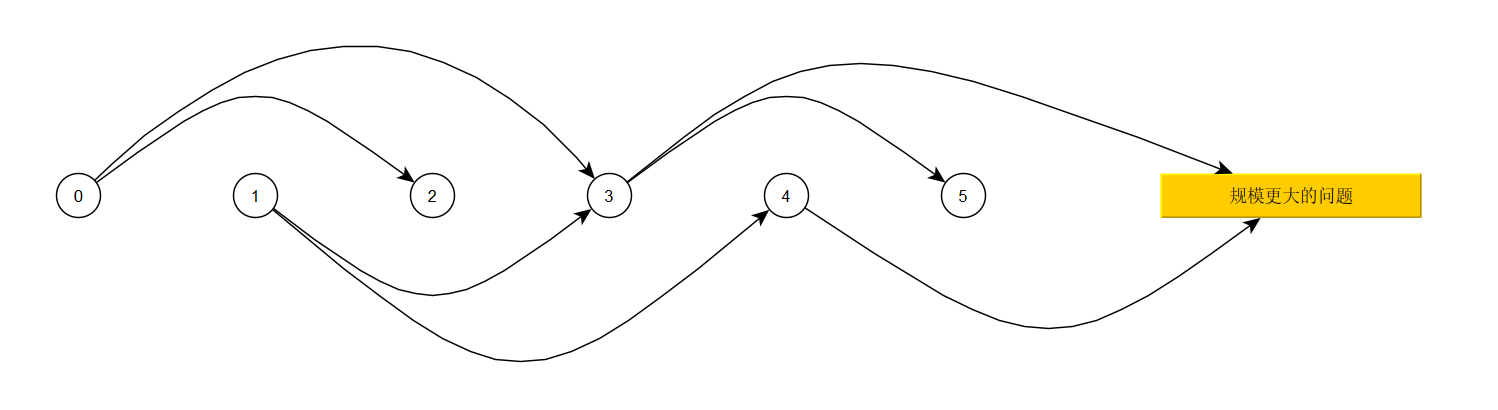
让我们尝试叫个小人来走一下楼梯,看看有多少办法能走到4号节点

从0开始，选择走1或2步，可以到达1或者2；然后是1节点，同样可以选择走一步或者两步到2或3节点，重复这个过程就得到了这样的一个图：

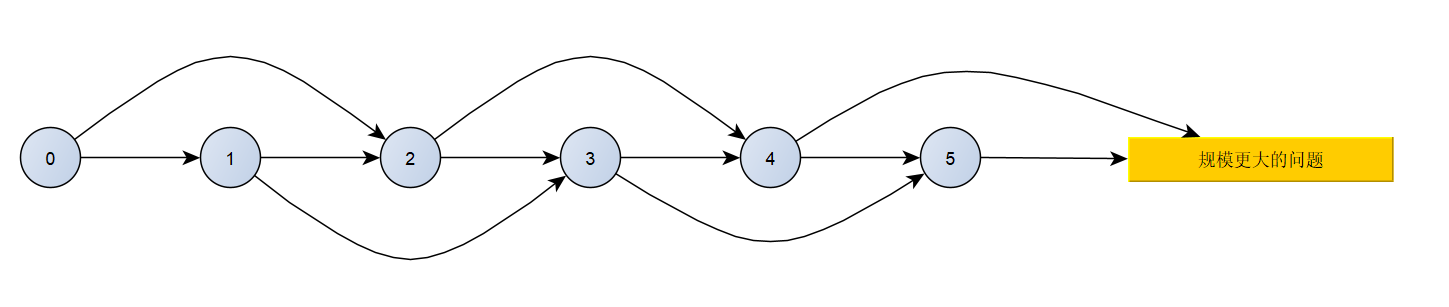这是一个状态转移图它就是状态转移图了。这样看还不够直观，不能直接数出来想要到达4节点能有多少种办法，于是把它转化成一个更加容易观察的树形结构：

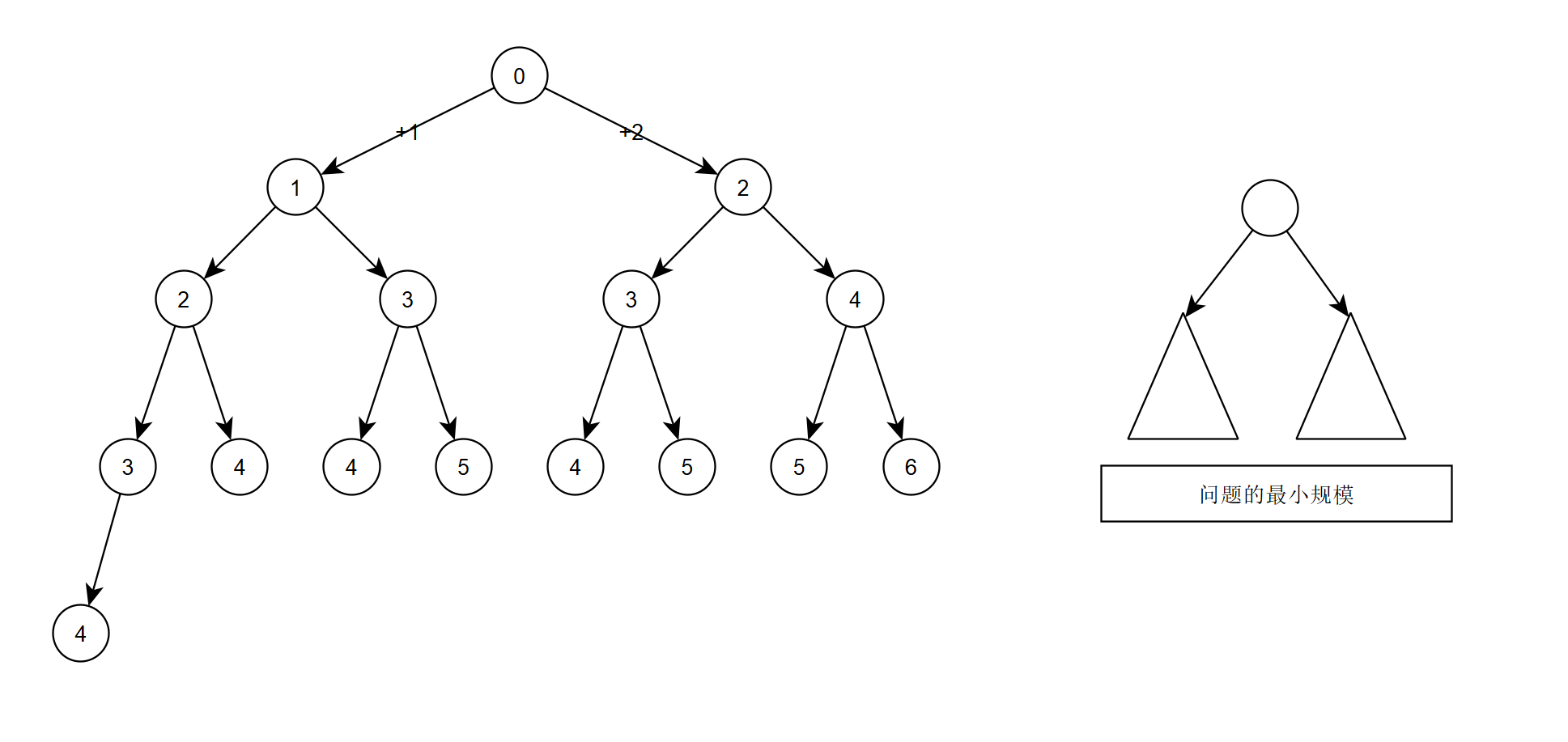
这两个图是逻辑等价的，状态转移图可以看作是这个决策树的重叠子结构的合并

首先理解这个题目的含义。选择了整数nums[i]之后你能获取它的点数，并且把这个元素数学相邻的元素删除：

选择 x：获得 x 的所有副本的总点数（即 x * (x的出现次数)）。

代价：不能再选择数学上相邻的 x-1 和 x+1。（选择之后必须至少间隔一次才能进行下次选择）

结合示例，我们能很自然的联想到计数排序，利用这个桶思想来对问题进行转化：计数排序结果数组每个元素乘以它的索引值，这就把它变为一个遍历数组找最优决策值的问题。

转化之后，这两个示例就变成了：

nums = [0,0,2,3,4] 选择idx = 2和idx = 4，sum=2+4

nums = [0,0,4,9,4] 选择idx = 3，sum=9

根据之前对题意的简单理解就有：

// 边界条件
dp[0] = 0                  // 没有数字时，点数为0
dp[1] = value[1]           // 只有数字1时，点数就是value[1]

// 状态转移方程 (对于 i >= 2)
dp[i] = max(dp[i-1], dp[i-2] + value[i])

那动态规划不就是选与不选和选择哪个的问题么？（至少绝大部分是符合路径累积与最优决策框架的）

//疑问：难道所有可以递归解决的问题都有封闭形式的动态转移方程么？

1.2 探索：一个新世界的轮廓

有限状态自动机就是这样的工具。我们在模拟决策与分析时画出来的那个图就是典型的有向无环图，至此，我们的核心嘉宾就到齐了。“链表是特殊的树，树是特殊的图”决策树就是有向无环图的一个典型。

第二章：基石概念：从生活隐喻到理论定义

2.1 有限状态机：不只是“自动”，更是“触发”

从游戏AI的案例引入：玩过砍怪兽游戏的同学都知道，游戏里的小怪是会巡逻的，当玩家出现在追击范围内，有的小怪会进行攻击行为；如果玩家离开追击范围一段时间（脱战），小怪则会返回巡逻点继续巡逻。那么，我们可以画出这样的概念图：

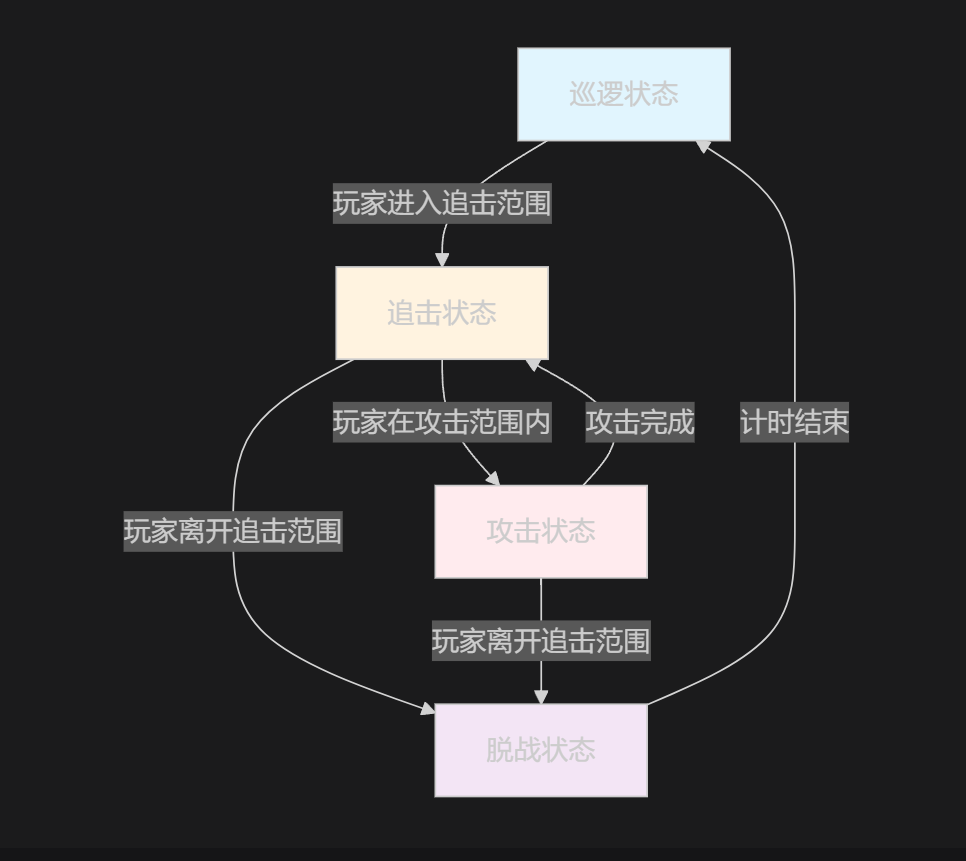这其中包含了怎样的信息呢？我们拎一条出来看看。首先是初始状态：巡逻状态；玩家进入追击范围，获得一个输入信号，触发自动切换状态——追击状态；攻击到玩家之后，攻击完成，仍在追击范围之内则继续攻击，进入循环——攻击玩家，直到玩家被击败。

以下是完整的状态转移表：

当前状态	输入信号	下一状态	游戏中的含义
PATROL	player_in_detection_range	CHASE	发现玩家，开始追击
CHASE	player_out_chase_range	DISENGAGE	玩家跑远，准备脱战
CHASE	player_in_attack_range	ATTACK	进入攻击距离，开始攻击
DISENGAGE	timer_expired	PATROL	脱战确认，返回巡逻
DISENGAGE	player_in_detection_range	CHASE	脱战中又发现玩家，继续追击
ATTACK	attack_finished	CHASE	攻击完成，回到追击状态

有限状态自动机，是一个五元组：M = (Q, Σ, δ, q₀, F)：

Q 定义了"能做什么"

Σ 定义了"感知到什么"

δ 定义了"如何反应"

q₀ 定义了"起始点"

F 定义了"理想状态"

在这个游戏ai的案例之中：

1. 状态集 Q
Q = {
    'PATROL',    # 巡逻状态
    'CHASE',     # 追击状态
    'DISENGAGE', # 脱战状态  
    'ATTACK'     # 攻击状态
}

2. 输入字母表 Σ
Σ = {
    'player_in_detection_range',  # σ₁: 玩家进入侦测范围
    'player_out_chase_range',     # σ₂: 玩家离开追击范围  
    'player_in_attack_range',     # σ₃: 玩家进入攻击范围
    'timer_expired',              # σ₄: 脱战计时器到期
    'attack_finished'             # σ₅: 攻击动作完成
}

3. 状态转移函数 δ
δ = {
    # (当前状态, 输入信号) → 下一状态
    ('PATROL',   'player_in_detection_range'): 'CHASE',
    ('CHASE',     'player_out_chase_range'):   'DISENGAGE',
    ('CHASE',     'player_in_attack_range'):   'ATTACK',
    ('DISENGAGE', 'timer_expired'):            'PATROL', 
    ('DISENGAGE', 'player_in_detection_range'): 'CHASE',
    ('ATTACK',    'attack_finished'):          'CHASE'
}

4. 初始状态 q₀
q₀ = 'PATROL'

5. 接受状态集 F
F = {'PATROL'}

2.2 有向无环图：计算过程的“时空沙盘”

当我们把爬楼梯问题的状态转移可视化时，得到的正是一个典型的有向无环图(DAG)。这个图不仅仅是一种可视化工具，更是整个计算过程的"时空沙盘"——它同时编码了问题的时间演进和空间结构。还是那张图：

这是一个状态转移图

//节点：所有可能的子问题状态
nodes = [0, 1, 2, 3, ..., n]

//边：状态转移的可能性
edges = {
    0 → 1 (走1步), 0 → 2 (走2步),
    1 → 2 (走1步), 1 → 3 (走2步), 
    2 → 3 (走1步), 2 → 4 (走2步),
    ...
}

为什么必须无环？
因为动态规划的核心思想是利用已经解决的子问题。如果图中存在环，比如从状态i能通过某种路径回到状态i，就意味着：

计算dp[i]时需要dp[i]本身的值
陷入无限递归的悖论
破坏了拓扑排序的基础

//疑问：所有DP问题都是无环的吗？

DAG作为"计算蓝图"

这个有向无环图实际上预先描绘了所有可能的计算路径：

节点：标记了每个需要计算的子问题
边：定义了子问题之间的依赖关系
拓扑序：天然给出了正确的计算顺序

2.3 动态规划：在"沙盘"上的"系统化寻优"

心法回顾：

"从小规模案例入手，寻找普遍规律"

让我们重新审视爬楼梯问题的思考流程：

最小案例：n=0时，有1种方法（不动）；n=1时，有1种方法
稍大规模：n=2时，可以从0走2步，或者从1走1步，共2种方法
发现模式：n=3时，方法数 = n=2时的方法数 + n=1时的方法数
普遍规律：dp[i] = dp[i-1] + dp[i-2]

这种统一性不仅存在于爬楼梯问题，而是贯穿了整个动态规划领域。无论问题表面如何变化，只要它能够被建模为在DAG上的系统化寻优，能够用有限状态自动机来描述其状态演进，那么它就适合用动态规划来解决。

这正是算法设计的美妙之处——在看似不同的问题背后，往往隐藏着相同的计算本质。

第三章：对感性认知的怀疑与粗略讨论

3.1 回顾疑问

//所有适用于递归的问题都能给出封闭形式的状态转移方程么？

3.1.1没有封闭形式状态转移方程的情况

a) 状态空间连续或无限

例如：某些最优控制问题，状态是连续函数，只能写成泛函方程（如 Hamilton–Jacobi–Bellman 方程），不是离散递推。

b) 历史依赖性较强

例如：在递归中如果解依赖于完整的路径历史（而不只是当前状态），那么状态必须包含历史信息，状态空间会指数膨胀，难以写出固定形式的有限项递推。

c) 问题不可分

某些递归问题虽然可以递归分解，但子问题之间互相影响复杂，无法用简单方程表达。

d) 非最优化类递归

例如 Ackermann 函数：

$A(m, n) = \begin{cases} n + 1 & \text{if } m = 0 \\ A(m - 1, 1) & \text{if } m > 0 \text{ and } n = 0 \\ A(m - 1, A(m, n - 1)) & \text{otherwise} \end{cases}$

它虽然是递归的，但不能写成固定前有限项的递推式，因为它依赖更深层的递归调用。

//难道所有的DP都没有环么？

3.1.2确实存在带有环的动态规划问题，它们突破了经典的DAG模型：

(这里只做简单的讨论）

例1：带负权边的最短路径问题

// 假设：
// vertices 是顶点数
// edges 是边数组，每个元素是 {u, v, weight}
// edge_count 是边的总数
// dist[] 是距离数组，已初始化为 INF，dist[source] = 0

// 核心逻辑：通过|V|-1次松弛操作处理可能的环
for (int i = 1; i <= vertices - 1; i++) {
    for (int j = 0; j < edge_count; j++) {
        int u = edges[j].u;
        int v = edges[j].v;
        int weight = edges[j].weight;
        
        if (dist[u] != INF && dist[u] + weight < dist[v]) {
            dist[v] = dist[u] + weight; // 可能通过环获得更短路径
        }
    }
}

环的意义：负权环意味着存在一条可以无限降低成本的路径，这打破了传统DAG的"无环"假设。Bellman-Ford算法通过限定松弛次数来"控制"环的影响，如果第|V|次松弛还能更新，就说明存在负权环。

例2：概率DP中的自环

// 假设：
// states 是状态数
// rewards[] 是即时奖励数组
// gamma 是折扣因子
// transition[][] 是转移概率矩阵
// V[] 是价值函数数组
// V_new[] 是新的价值函数数组

// 状态转移包含自环概率
for (int s = 0; s < states; s++) {
    double sum = 0.0;
    for (int s_prime = 0; s_prime < states; s_prime++) {
        sum += transition[s][s_prime] * V[s_prime];
    }
    V_new[s] = rewards[s] + gamma * sum;
    // 其中 transition[s][s] ≠ 0 就形成了数学自环
}

环的意义：在概率模型中，状态可能以非零概率保持在原地，这在数学上形成了自环。这种环不是bug而是特性，它反映了现实世界中"状态可能不变"的客观规律。求解时我们通过迭代收敛来处理这种循环依赖。

例3：迭代优化算法

// 假设：
// states 是状态数
// actions 是动作数
// gamma 是折扣因子
// rewards[][] 是奖励函数 rewards[s][a]
// transition[][][] 是转移概率 transition[s][a][s_next]
// V[] 是价值函数数组

// 核心的迭代更新过程
while (1) {
    double max_diff = 0.0;
    
    for (int s = 0; s < states; s++) {
        double best_value = -DBL_MAX;
        
        // max_action[期望收益 + γ * V[下一个状态]]
        for (int a = 0; a < actions; a++) {
            double expected_value = 0.0;
            for (int s_next = 0; s_next < states; s_next++) {
                expected_value += transition[s][a][s_next] * V[s_next];
            }
            double action_value = rewards[s][a] + gamma * expected_value;
            if (action_value > best_value) {
                best_value = action_value;
            }
        }
        
        double old_value = V[s];
        V[s] = best_value;
        double diff = fabs(old_value - V[s]);
        if (diff > max_diff) {
            max_diff = diff;
        }
    }
    
    // 检查收敛
    if (max_diff < CONVERGENCE_THRESHOLD) {
        break;
    }
    // 在状态图的环中多次迭代直到收敛
}

环的意义：值迭代算法本质上是在状态图的环上"绕圈"，每次迭代都利用前一次迭代的结果。这种环不是结构上的缺陷，而是算法收敛的必经之路。