从0开始学习R语言-Day56--空间变系数模型

对于涉及到空间相关性分析的数据来说，直接对其做杜宾模型的拟合，有时候很难解释有些变量的p值或是否收敛，因为许多变量的联系以及数据特征在拟合的过程中被消化掉了。

而用不同的方法和模型去一步步测试特性，不仅可以证明课题或数据有无研究下去的意义，还可以帮我们节省工作量，确定研究的方向。

以下是一个例子：

# 加载包
library(sp)
library(spgwr)
library(ggplot2)
library(sf)

# 生成模拟数据
set.seed(123)
lon <- runif(100, 0, 10)
lat <- runif(100, 0, 10)
x <- rnorm(100, mean = 10, sd = 2)
beta <- 2 + 0.5 * lon - 0.3 * lat
y <- beta * x + rnorm(100, sd = 1)
data <- data.frame(y, x, lon, lat)

# 转换为 SpatialPointsDataFrame
coordinates(data) <- c("lon", "lat")

# 拟合GWR模型
bw <- gwr.sel(y ~ x, data = data, method = "aic")
gwr_model <- gwr(y ~ x, data = data, bandwidth = bw)

# 确保 SDF 是空间对象
gwr_sf <- st_as_sf(gwr_model$SDF, coords = c("lon", "lat"))


ggplot(gwr_sf) +
  geom_sf(aes(color = x), size = 3) +
  scale_color_gradientn(colors = heat.colors(100)) +
  labs(title = "x的系数空间变化")

输出：

Bandwidth: 5.326436 AIC: 800.4894 
Bandwidth: 8.60975 AIC: 835.84 
Bandwidth: 3.297236 AIC: 719.3295 
Bandwidth: 2.043122 AIC: 599.3783 
Bandwidth: 1.268037 AIC: 500.6082 
Bandwidth: 0.7890076 AIC: 475.9371 
Bandwidth: 0.603189 AIC: 533.1183 
Bandwidth: 0.9808626 AIC: 473.1434 
Bandwidth: 0.9165835 AIC: 470.9509 
Bandwidth: 0.9040195 AIC: 470.8164 
Bandwidth: 0.8927252 AIC: 470.7908 
Bandwidth: 0.8951735 AIC: 470.7884 
Bandwidth: 0.8952919 AIC: 470.7884 
Bandwidth: 0.8952512 AIC: 470.7884 
Bandwidth: 0.8952512 AIC: 470.7884

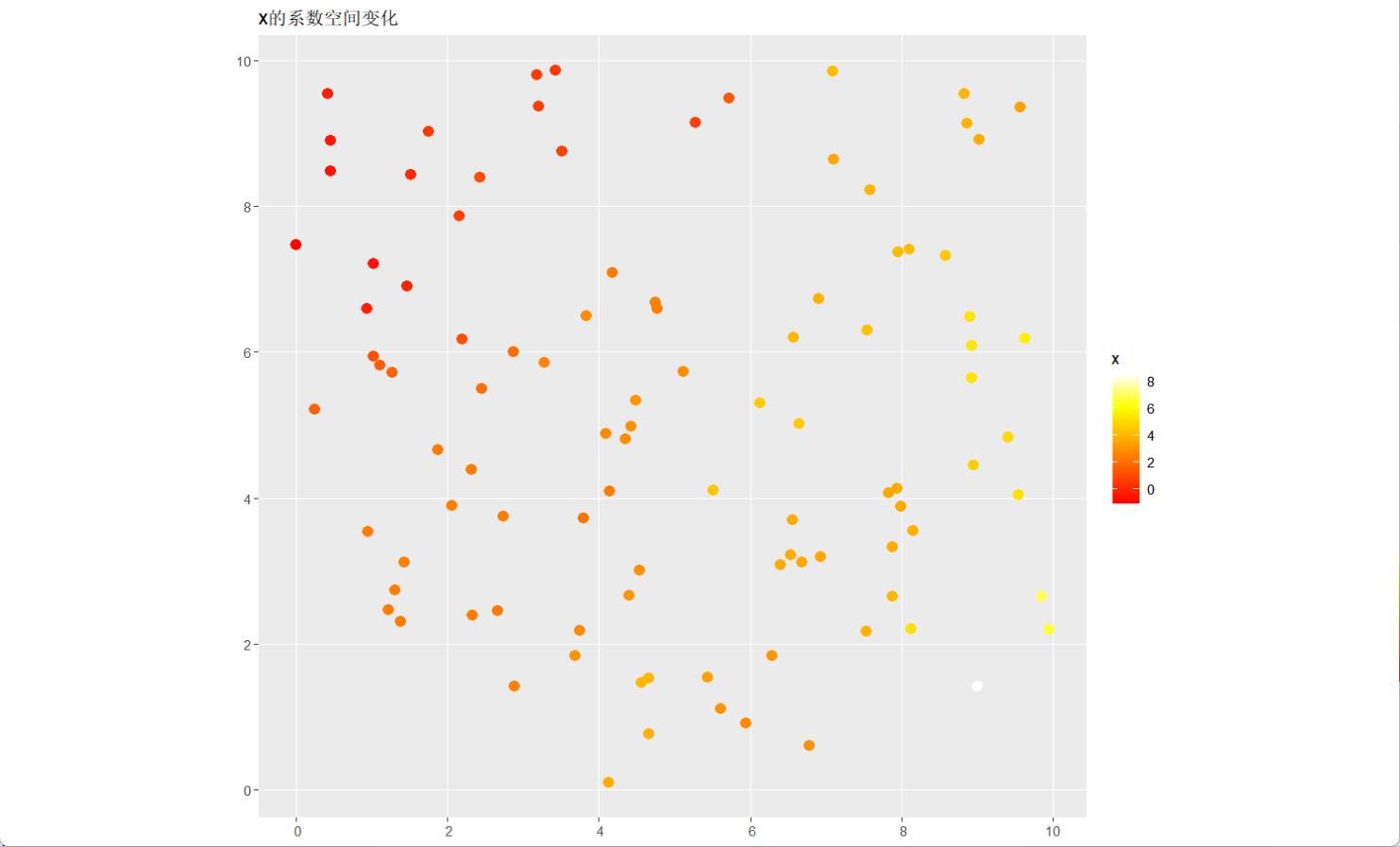
输出表明，两边区域的数据在分布上的颜色和系数并不对称，存在明显的空间差异，也就是说，x变量对因变量的影响在空间上具有显著的异质性和梯度分布特征。