Meet-in-the-Middle（折半搜索算法）

貌似没什么可讲的。。。。。

算法简介

常见的翻译为「折半搜索」、「双向搜索」或「中途相遇」。

它适用于输入数据较小，但还没小到能直接使用暴力搜索的情况。

算法流程

Meet in the middle 算法的主要思想是将整个搜索过程分成两半，分别搜索，最后将两半的结果合并。

特征

数据范围：$n\ge 30$ （爆搜（$2^n$）不可过）$n\le 50$（折半搜索($2^{\frac{n}{2}}$)可过）
时间复杂度：$2^{\frac{n}{2}}$

例题

1.ABCD(SPOJ)

大意：在数组 $a$ 中有多少六元组满足 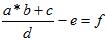（$n\le 100$）
$n^6$ 直接起飞，所以需要折半（$n^3$ 可过）。
化简得到：$f(e+d)=ab+c$，可以预处理出所有 $ab+c$ 和 $a(b+c)$ 有多少值
则枚举 $d,e,f$ 即可。
PS：注意只能枚举 $d,e,f$ 因为 $d$ 做分母不能为 $0$
代码：略

2.Ice Hockey World Championship（黑暗爆炸4800）

大意：有n个物品，m块钱，给定每个物品的价格，求买物品的方案数。（不买也算一种）
$n\le 50,m\le 10^{18}$，看到题目首先想到背包，但是 $m\le 10^{18}$
直接GG，又看到 $n\le 50$ 很容易想到双向搜索。
先跑一遍前 $\frac{n}{2}$ 的暴搜，把每种价格都存下来，然后跑后 $\frac{n}{2}$ 的暴搜，算出价格和 $tot2$ 之后，就查找前 $\frac{n}{2}$ 个数中的价格和有多少 $tot1$ 满足 $tot1+tot2\le m$，这个可以使用二分来做。
PS：无论是使用二分函数还是手写二分都需要排序。。。。。
代码：

void dfs1(int x, LL tot) {
	if (tot > m) return;
	if (x == n / 2 + 1) {
		p[++L] = tot;
		return;
	}
	if (tot + a[x] <= m) dfs1(x + 1, tot + a[x]);
	dfs1(x + 1, tot);
}

void dfs2(int x, LL tot) {
	if (tot > m) return;
	if (x == n + 1) {
		ans += upper_bound(p + 1, p + 1 + L, m - tot) - p - 1;
		return; 
	}
	if (tot + a[x] <= m) dfs2(x + 1, tot + a[x]);
	dfs2(x + 1, tot);
}