【机器学习】案例1.2——DBSCAN聚类

一、项目背景

在无监督机器学习领域，聚类是核心任务之一，用于将无标签数据按内在相似性划分为不同簇。传统聚类算法（如K-Means）存在明显局限性：

1. 需预先指定聚类数量，实际场景中难以精准确定；
2. 仅能处理凸形状聚类，对不规则形状、密度不均匀的数据集效果差；
3. 无法识别噪声点，对异常值敏感。

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，核心优势在于：

• 无需预先指定聚类数量；
• 可自动发现任意形状的聚类簇；
• 能识别数据中的噪声点（异常值）；
• 对密度差异的数据集适应性更强。

本项目通过生成模拟数据集，系统验证DBSCAN核心参数（邻域半径epsilon、最小样本数min_samples）对聚类结果的影响，直观展示算法的参数敏感性和聚类效果，解决传统聚类算法的局限性验证问题。

二、解决问题的方案

1. 数据层：生成含4个不同密度聚类中心的模拟二维数据集，标准化消除量纲影响；
2. 参数层：设计6组(epsilon, min_samples)参数组合，验证核心参数对聚类结果的影响；
3. 模型层：基于每组参数训练DBSCAN模型，区分核心样本、非核心样本和噪声点；
4. 可视化层：将聚类结果可视化，用不同颜色区分簇、黑色标记噪声、大尺寸标记核心样本；
5. 分析层：通过打印聚类数量和可视化结果，分析参数对聚类效果的影响规律（epsilon越大邻域越广，易合并簇；min_samples越大密度要求越高，易识别更多噪声）。

三、带详细注释的完整代码

#!/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler


def expand(a, b):
    """
    扩展坐标轴范围的辅助函数，让可视化结果更美观（避免数据点贴坐标轴）
    :param a: 坐标轴最小值
    :param b: 坐标轴最大值
    :return: 扩展后的最小值、最大值（扩展原范围的10%）
    """
    d = (b - a) * 0.1
    return a-d, b+d


if __name__ == "__main__":
    # ===================== 1. 数据准备 =====================
    N = 1000
    centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
    data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)
    data = StandardScaler().fit_transform(data)

    # ===================== 2. 设计参数组合 =====================
    params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))

    # ===================== 3. 可视化配置 =====================
    matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    matplotlib.rcParams['axes.unicode_minus'] = False

    plt.figure(figsize=(12, 8), facecolor='w')
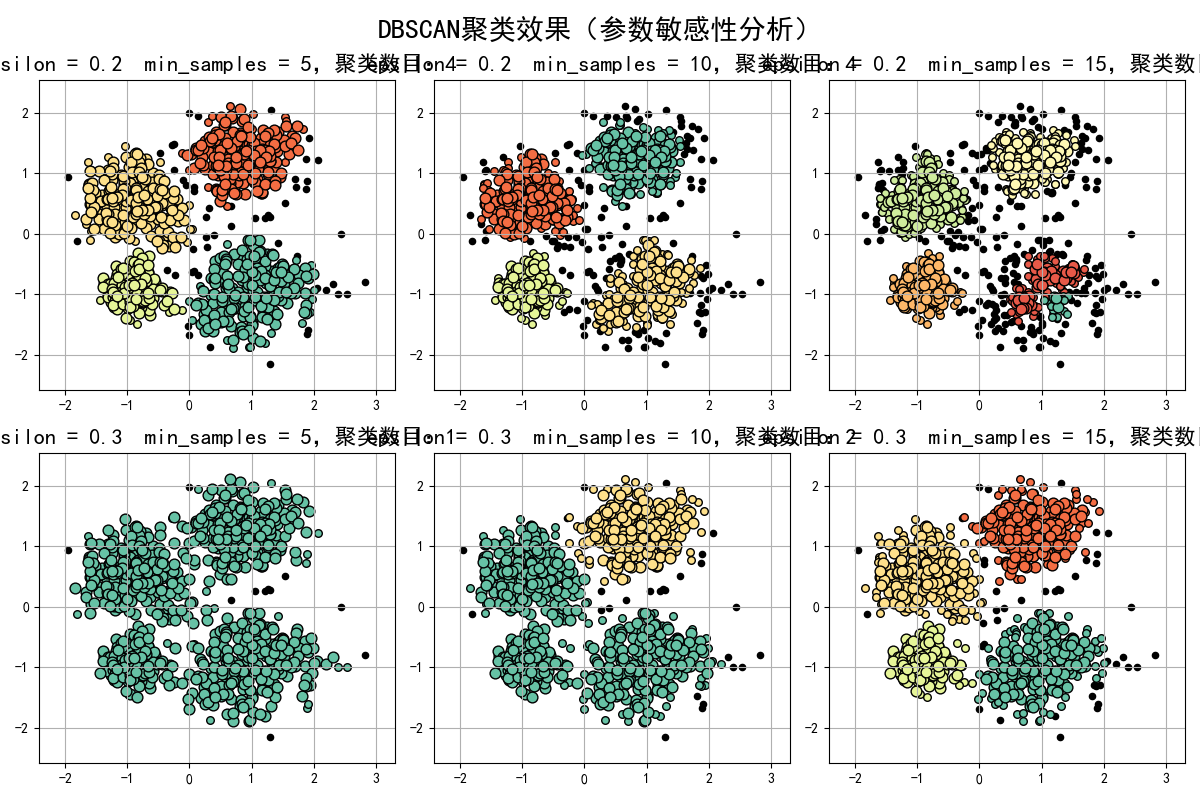
    plt.suptitle(u'DBSCAN聚类效果（参数敏感性分析）', fontsize=20)

    # ===================== 4. 遍历参数训练模型并可视化 =====================
    for i in range(6):
        eps, min_samples = params[i]
        model = DBSCAN(eps=eps, min_samples=min_samples)
        model.fit(data)
        y_hat = model.labels_

        core_indices = np.zeros_like(y_hat, dtype=bool)
        core_indices[model.core_sample_indices_] = True

        y_unique = np.unique(y_hat)
        n_clusters = y_unique.size - (1 if -1 in y_hat else 0)
        print(f"参数(eps={eps}, min_samples={min_samples})：标签类型={y_unique}，聚类簇的个数为：{n_clusters}")

        plt.subplot(2, 3, i+1)
        clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size))

        # 核心修改：将c=clr改为color=clr，消除RGB序列警告
        for k, clr in zip(y_unique, clrs):
            cur = (y_hat == k)
            if k == -1:
                # 噪声点用黑色，c='k'是简写，无警告
                plt.scatter(data[cur, 0], data[cur, 1], s=20, c='k', label='噪声点' if i==0 else "")
                continue
            # 非噪声样本：用color指定统一颜色，替代c参数
            plt.scatter(data[cur, 0], data[cur, 1], s=30, color=clr, edgecolors='k')
            # 核心样本：同样用color参数
            plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], 
                        s=60, color=clr, marker='o', edgecolors='k')

        # 调整坐标轴范围
        x1_min, x2_min = np.min(data, axis=0)
        x1_max, x2_max = np.max(data, axis=0)
        x1_min, x1_max = expand(x1_min, x1_max)
        x2_min, x2_max = expand(x2_min, x2_max)
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title(u'epsilon = %.1f  min_samples = %d，聚类数目：%d' % (eps, min_samples, n_clusters), fontsize=16)

    plt.tight_layout()
    plt.subplots_adjust(top=0.9)
    plt.show()

四、核心结果分析

1. epsilon的影响：相同min_samples下，epsilon从0.2增至0.3时，邻域范围扩大，更多样本被归为同一簇，聚类数目减少（易合并低密度簇）；
2. min_samples的影响：相同epsilon下，min_samples从5增至15时，密度阈值提高，更多样本被判定为噪声，聚类数目可能减少（高密簇保留，低密簇被拆分为噪声）；
3. 噪声识别：标签为-1的样本始终以黑色显示，min_samples越大、epsilon越小，噪声点数量越多。

该代码通过系统化的参数测试和可视化，清晰展示了DBSCAN的核心特性，为实际场景中调参提供了直观参考。

运行结果：

'''
参数(eps=0.2, min_samples=5)：标签类型=[-1  0  1  2  3]，聚类簇的个数为：4
参数(eps=0.2, min_samples=10)：标签类型=[-1  0  1  2  3]，聚类簇的个数为：4
参数(eps=0.2, min_samples=15)：标签类型=[-1  0  1  2  3  4]，聚类簇的个数为：5
参数(eps=0.3, min_samples=5)：标签类型=[-1  0]，聚类簇的个数为：1
参数(eps=0.3, min_samples=10)：标签类型=[-1  0  1]，聚类簇的个数为：2
参数(eps=0.3, min_samples=15)：标签类型=[-1  0  1  2  3]，聚类簇的个数为：4

进程已结束，退出代码为 0
'''