动手学深度学习V2.0(Pytorch)——29.2 ResNet为什么能训练出1000层的模型

29.2 1. ResNet为什么能训练出1000层的模型

https://www.bilibili.com/video/BV1554y157E3

这部分没有PPT，所以简单做一些记录和自己绘图

---

1.1 Resnet是如何处理梯度消失，使得其可以训练1000层的模型

之前说到避免梯度消失的方式有几种，

• 有一种避免梯度消失的办法是 乘法变加法，ResNet就是这么做的，特别是Residual Connection

接下来主要讨论 Residual是如何处理梯度消失的：

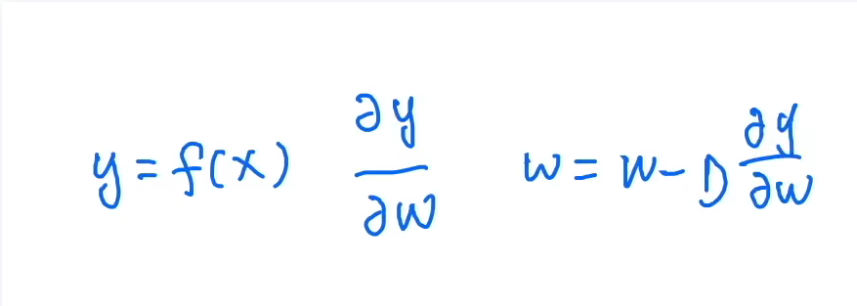
如上图所示，

• 假设已经有一个网络，用$y=f(x)$表示，$x$是输入，$y$是输出。$f$就是函数映射，比如是10个卷积层之类的。
• 那么如果这个$f$中比如有个参数$w$（可能不止一个值，是一个Tensor）， 则损失函数对$w$求导就可以表示为：$\frac{\partial y}{\partial w}$
  • 这里暂时不考虑那么详细的损失函数了，反正损失函数里肯定有$y$，无非就是再多点东西
  • 另外假设这里的$w$就是靠近底层的一个参数，就这样表示计算梯度了
• 需要保证$\frac{\partial y}{\partial w}$求导出的结果/梯度，不会特别小。因为在梯度更新时，会根据$$w=w-\eta \frac{\partial y}{\partial w}$$来更新参数$w$，如果梯度很小，那么调节学习率也不好调，数值稳定性会发生一些问题（比如梯度消失，那网络其实就死了，权重不会更新了）。所以我们希望计算出来的梯度不要太小

---

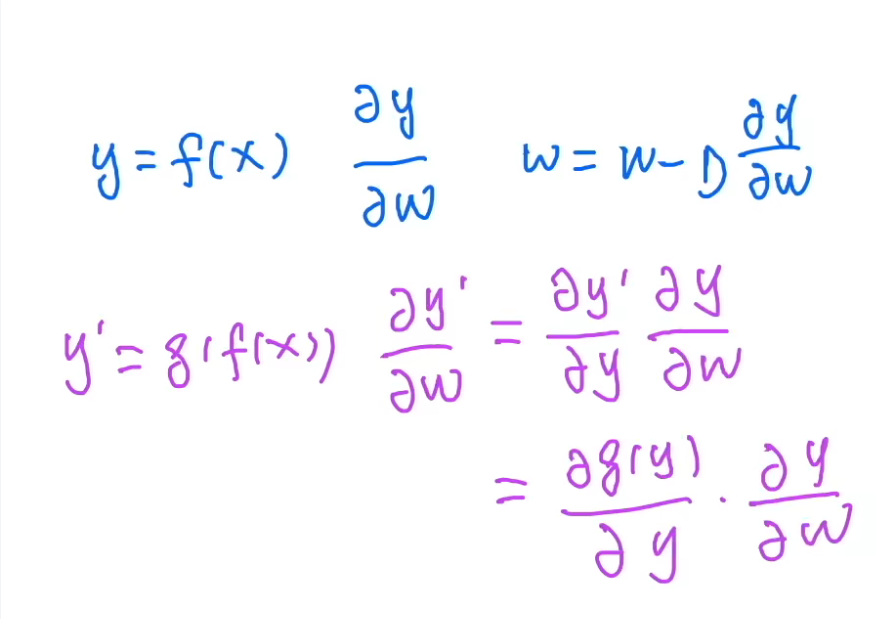
接下来，假设在这个网络上面再加一些层，也就是对$f$进行扩充，把这个函数变得更复杂，加东西。

• 图像中紫色笔写的，假设加了一个$g(x)$，那么加之后就变成$y^{\prime }=g(f(x))$，$y^{\prime }$只是个记号表示，不是一阶导数。比如就是在$f(x)$这10个卷积层上面，再加了10个卷积层（$g(x)$）
• 那么还是去看$f(x)$里的$w$(靠近底层/数据端的那个参数)，根据复合函数求导的链式法则,它的求导就变成了：
  $$\begin{array}{rl}\frac{\partial y^{\prime }}{\partial w}& =\frac{\partial y^{\prime }}{\partial y}\frac{\partial y}{\partial w}\\ & =\frac{\partial g(y)}{\partial y}\frac{\partial y}{\partial w}\end{array}$$
• 从结果中可以看到，梯度的右半部分，和之前是一样的；问题出现在左半部分，相当于新加的那部分层对$y$进行求导，也就是$g(y)$这个网络对它的输入$y$求导。
• 如果用的是拟合能力特别强的网络，比如AlexNet，靠近输出层的部分是三个超大的FC层，那么左半部分的这个$\frac{\partial g(y)}{\partial y}$会很快变得特别小，
  • 解释一下，$g(y)$是$y=f(x)$上面的层，相对来说，是高层/靠近输出端的层，所以在求梯度的时候，高层参数的导数会更大，也就是参数更新会快。参数更新快，那么损失函数就在减小（和$y$一样，这里也把$$y^{\prime }$粗略的作为损失函数），那么$\frac{\partial g(y)}{\partial y}$就会很快变小。
  • 带来的问题就是，底层的梯度，更小！（一个很小的数，乘以 加层之前的梯度，那么之前底层的梯度，也就会更小）
• 当梯度很小的时候，要么增大学习率，
  • 但是增大也不一定特别有用，因为不能增的太大，
  • $g(y)$里的$w$合适的学习率 ≠ $f(x)$里的$w$的合适的学习率，如果增的太大，那么$g(y)$里的$w$就很可能梯度爆炸，整个就不稳定了
• 当网络越深，那么越靠近数据层/底层，梯度就会越小，越容易出问题！（所以网络变深的时候就非常容易梯度消失）
  • 这是由于层之间是函数嵌套的关系，所以求导的时候都是乘法
  • 考虑将乘法变成加法，也就是把网络中层的嵌套，变成网络中层的并行！

---

现在看一下resnet是怎么解决梯度消失的问题的，绿色笔

假设resnet这个网络，输出用$y^{\prime \prime }$表示（不是$y$的二阶表示，虽然这个表示真的很有歧义），那么可以表示为：$$y^{\prime \prime }=f(x)+g(f(x))$$
其实就是那个残差链接干的事情，就是residual block的公式，$g(x)=x+f(x)$，只是residual block的这个公式里的$x$，本身也是下面一个子网络的输出。
$$\begin{array}{rl}{y}^{\prime \prime }=& f(x)+g(f(x))\\ g(x)=& x+f(x)\end{array}$$对照一下这两个公式，则第二行的$x$就相当于第一行的$f(x)$,第二行的$f()$就相当于第一行的$g()$。其实是一样的
另外，化简一下：
$$y^{\prime \prime }=f(x)+g(f(x))=y+y^{\prime }$$
那么此时求导结果其实就是：
$$\frac{\partial y^{\prime \prime }}{\partial w}=\frac{\partial y}{\partial w}+\frac{\partial y^{\prime }}{\partial w}$$

• 加法的左项就是最原始的底层求导结果，右项是加了层之后的结果
• 左边一直是那么大，右边就算乘上了高层的导数导致$\frac{\partial y^{\prime }}{\partial w}$整体比较小，也没关系啊，我原始的左边的导数一直存在！ （右边那个乘积大小我都不care了，再小我左边还有个大的顶着呢，天塌下来高个子顶着🤓）
• 大数$+$小数还是等于大数，但是大数$\times$小数就有可能变成小数了

---

总结

• 这就是这个residual connection起到的作用，这个跳转连接保证了底层的梯度，不会比加新层（梯度乘积）之前小，不一定会变大，但是一定不会变得更小。
  • 沐神的评论：resnet后面出了很多论文来分析residual connection。上周视频是从函数嵌套，这次是补了之前讲梯度时埋的一个坑。当然还有很多别的角度解释，原始论文走的是residual这一条
  • 确实看起来很像，RNN中越靠后的时间步，对前面的信息记住的越少，都是因为乘法导致的逐渐遗忘，小数越来越小（梯度消失），大数越来越大（梯度爆炸）
• skip connection（在resnet中，叫做residual connection ）。直观上来看，

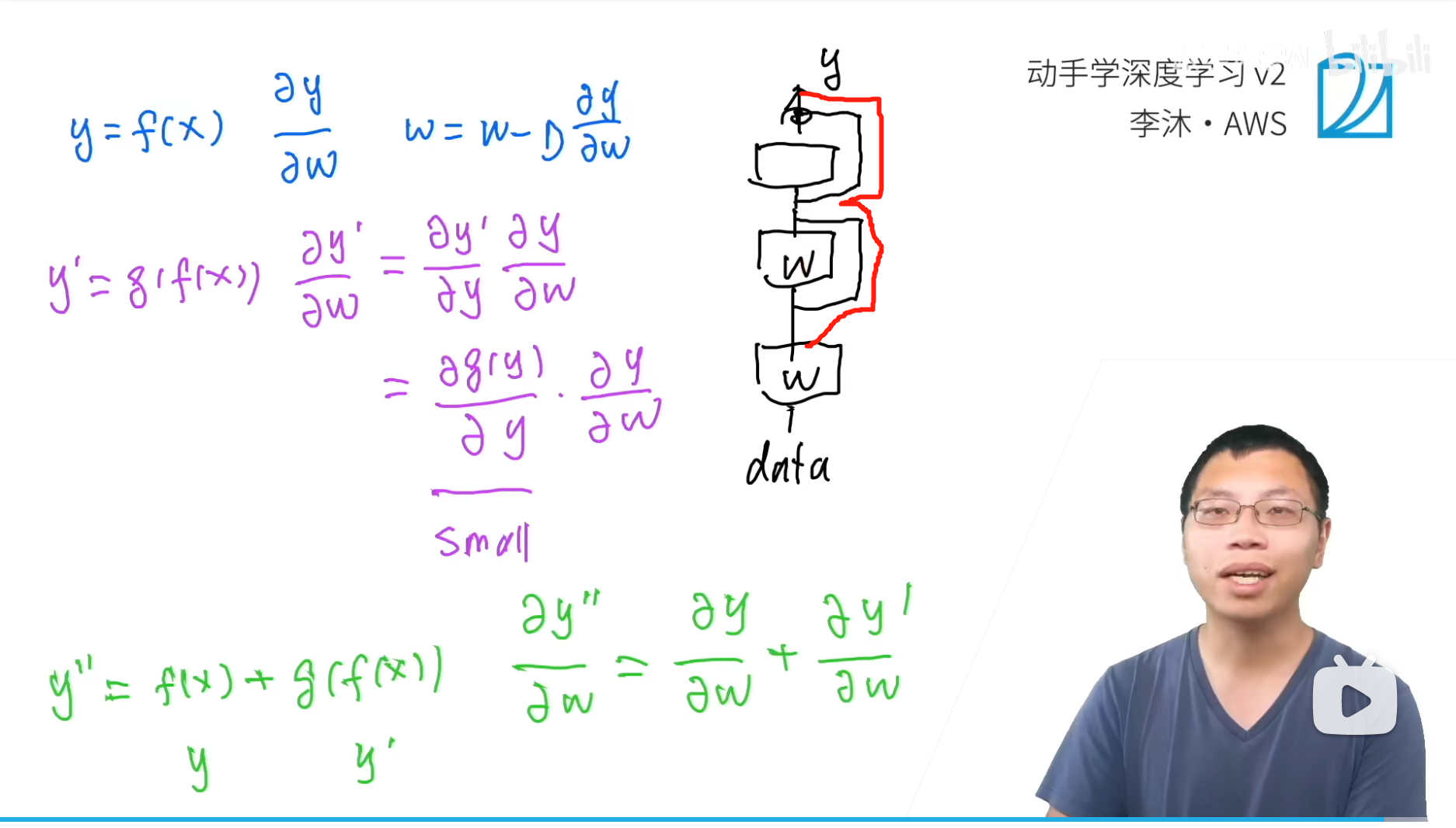
• 黑色线，每一个矩形+右侧的连线都是一个residual block（里面有两层卷积），
• 最下面是输入的数据层，最上面是输出层
• 靠近数据段的参数是比较难训练的，因为梯度消失的问题
• 但是加入residual connection之后，靠近数据层的权重，相当于有了一条新的从$y$直接到data的高速公路（不经过卷积层这些，图中红色的线），原来的路（经过卷积层）梯度可以很小，但是有了这个跳转连接之后，有了梯度的加法，那么靠近数据层的梯度就不会很小。

这是从梯度方面对residual connection的作用进行了一个解释，之前是从函数解空间的角度

---

1.2 弹幕里的一些说法

1. resnet文章中说不是由于梯度消失引起的退化问题

• 我也记得，之前都说BN是解决梯度消失的，控制每层的分布尽量一致，保证数值稳定性。
• 参考教材文档的小结：

  • 学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
  • 残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
  • 利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
  • 残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。

• 按照一般的说法，resnet最大的贡献就是那个梯度高速通道（借助残差块直接从上一stage输出连接到下一stage输入，即高速通道）

29.2 2. Q&A

https://www.bilibili.com/video/BV1554y157E3?p=2

2.1 学习率可不可以让靠近输出的小一些，让靠近输入的大一些，这样会不会就可以缓解梯度消失的问题？（layerwise）

• 这个问题其实就是表达：能不能让每层的梯度都不一样（这样其实非常直接，与其间接修改为加法避免梯度减小，直接把每层的lr变得不一样，越靠近底层，lr越大，不是更直接吗？）
• 有很多layerwise的方法，但是不好调（实用性不佳），相当于为了调节每层的学习率，要加入一个新的Hyperparameter，比如：靠近输入的要调大，调多大呢？靠近输出要调小，调多小呢？？ 超参这种东西，不确定性很大，试验代价很高；
• 相比于结构性（加一个residual block，调整网络结构）这种确定的东西，后者更加可控的一点，所以大家宁可去选择这种可控的结构tricks，也没有去选择调节超参这种吃力还不讨好的活。
• 另外，通过调节学习率来调节参数更新是有局限性的，比如梯度算下来是个很小的数字，那如果lr调节超过float32位，那么就会出现一些数值表示的问题。（计算机的数值表示，这就是操作系统和底层指令集的问题了，不是算法工程师可以解决的了）如果使用的是float16，那问题就会更明显。

layer wise相关的资料

• 知乎话题：Layer-Wise Training和Backpropagation有何本质区别？
• 简书文章：栈式自编码器的无监督逐层贪婪预训练(greedy layer-wise pre training)
• 优快云文章：深度学习: greedy layer-wise pre-training (逐层贪婪预训练)
• 出自论文：Yoshua Bengio（AI三巨头之一）——Greedy Layer-Wise Training of Deep Networks

弹幕里一句话

rmsprop可以，我记得adagrad的learning rate就是单调递减的