代码随想录算法训练营 day23| ● 669. 修剪二叉搜索树 ● 108.将有序数组转换为二叉搜索树 ● 538.把二叉搜索树转换为累加树

---

前言

迭代法都没看主要是669和538【538很简单】

669. 修剪二叉搜索树

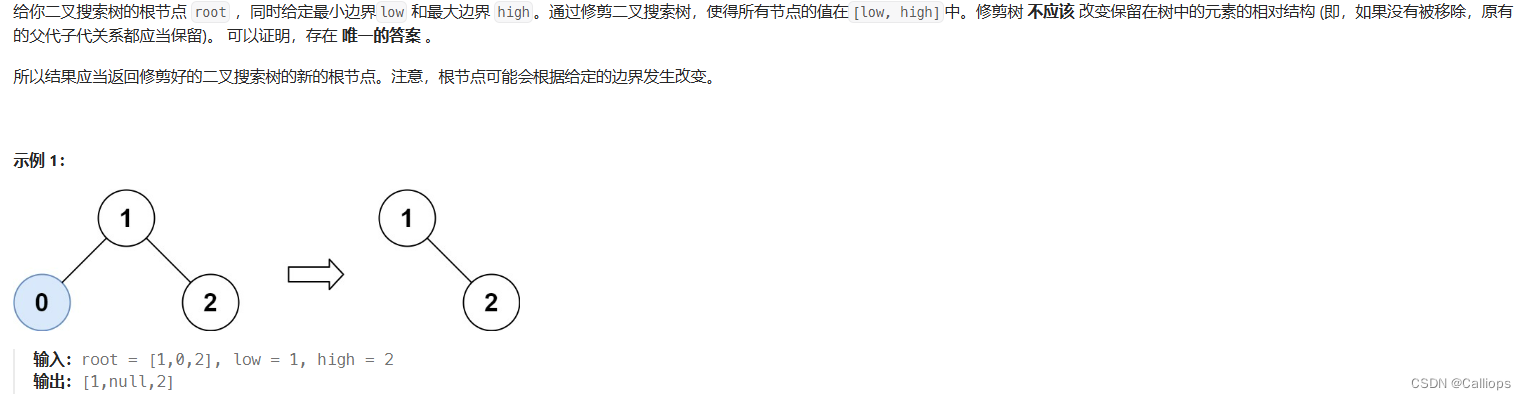
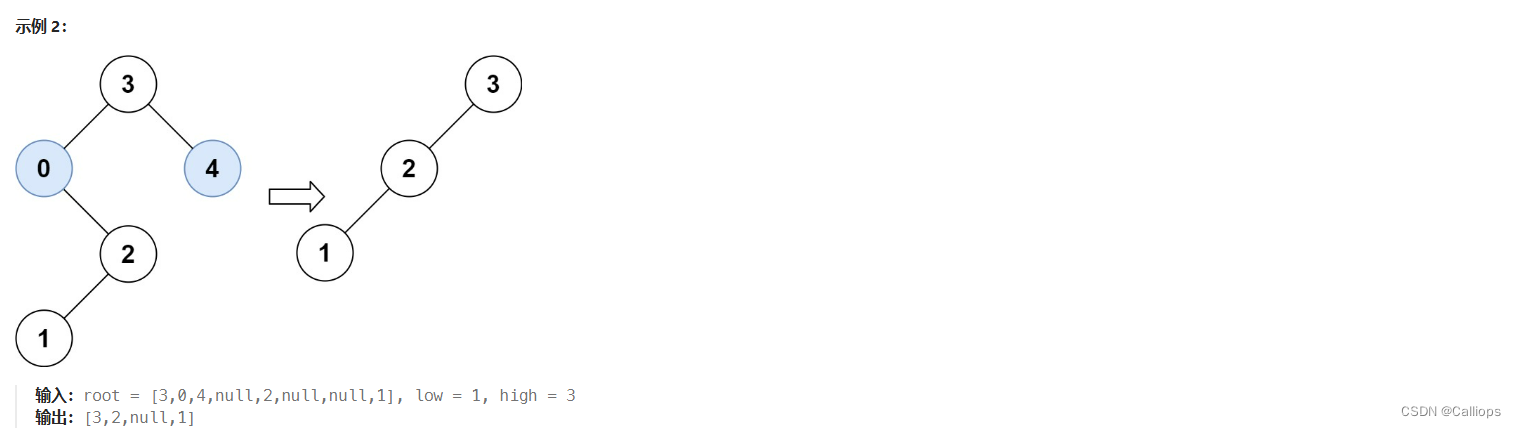
思路

不用看教程，思路很清晰
💖总体思路【单层递归逻辑】

1. 如果当前节点的值小于low，就处理root的右子树（因为左子树一定不符合），返回右子树的修剪结果，也就是return traversal（root.right）
2. 如果root的val大于high的话，就处理root的左子树（因为右子树一定不符合了），返回左子树修剪之后的结果，也就是return traversal（root.left）
3. 如果root的val处于区间之间，需要修剪他的左右子树，也就是root.left = traversal(root.left)，右边子树同理。
   终止条件：如果为null，返回null

方法一 递归法

class Solution(object):
    def trimBST(self, root, low, high):
        """
        :type root: TreeNode
        :type low: int
        :type high: int
        :rtype: TreeNode
        """
        if root == None: return None
        if root.val < low: 
            return self.trimBST(root.right,low,high)
        if root.val > high:
            return self.trimBST(root.left,low,high)
        if root.val<= high and root.val>=low:
            root.left = self.trimBST(root.left,low,high)
            root.right = self.trimBST(root.right,low,high)
            return root

方法二 迭代法

108.将有序数组转换为二叉搜索树

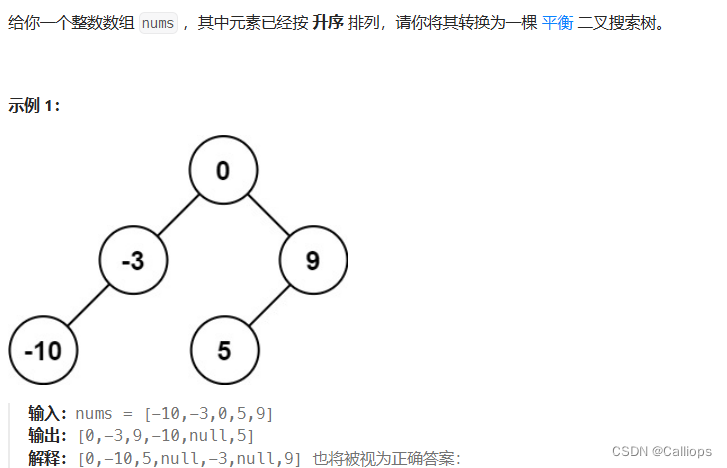
本题掌握递归法就够了，递归法比较复杂，升级版本；

思路

递归三部曲

1. 传入返回值：传入的是指向数组的指针，和范围；函数返回的是由这个范围内的数组构成的二叉树的根节点；
2. 终止条件：如果传入的数组范围中left>right，那就返回none
3. 单层递归逻辑：找到中间节点，作为root，root-left为左边区间构建的二叉树，右边同理

注意点

1. . 为了保证构造的是平衡二叉树，所以根节点是中间的值
2. . 注意传入的数组范围区间：本题中定义的是左闭右闭

方法一 递归法

写代码注意点：

1. 因为是左闭右闭的，所以判断迭代终止条件为left大于right
2. 传入的只是数组，而不是节点，这个要注意

class Solution(object):
    def traversal(self,left,right):
        if left > right: 
            return None 
        mid = (left + right)//2
        node = TreeNode(val = self.nums[mid])
        node.left = self.traversal(left,mid-1)
        node.right = self.traversal(mid+1,right)
        return node
    def sortedArrayToBST(self, nums):
        """
        :type nums: List[int]
        :rtype: TreeNode
        """
        self.nums = nums
        root = self.traversal(0,len(nums)-1)
        return root
 # 精简版 传递切片
 class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        if not nums:
            return
        mid = len(nums) // 2
        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[:mid])
        root.right = self.sortedArrayToBST(nums[mid + 1 :])
        return root       

方法二 迭代法

本题迭代法比较困难，就不用放了。

538.把二叉搜索树转换为累加树

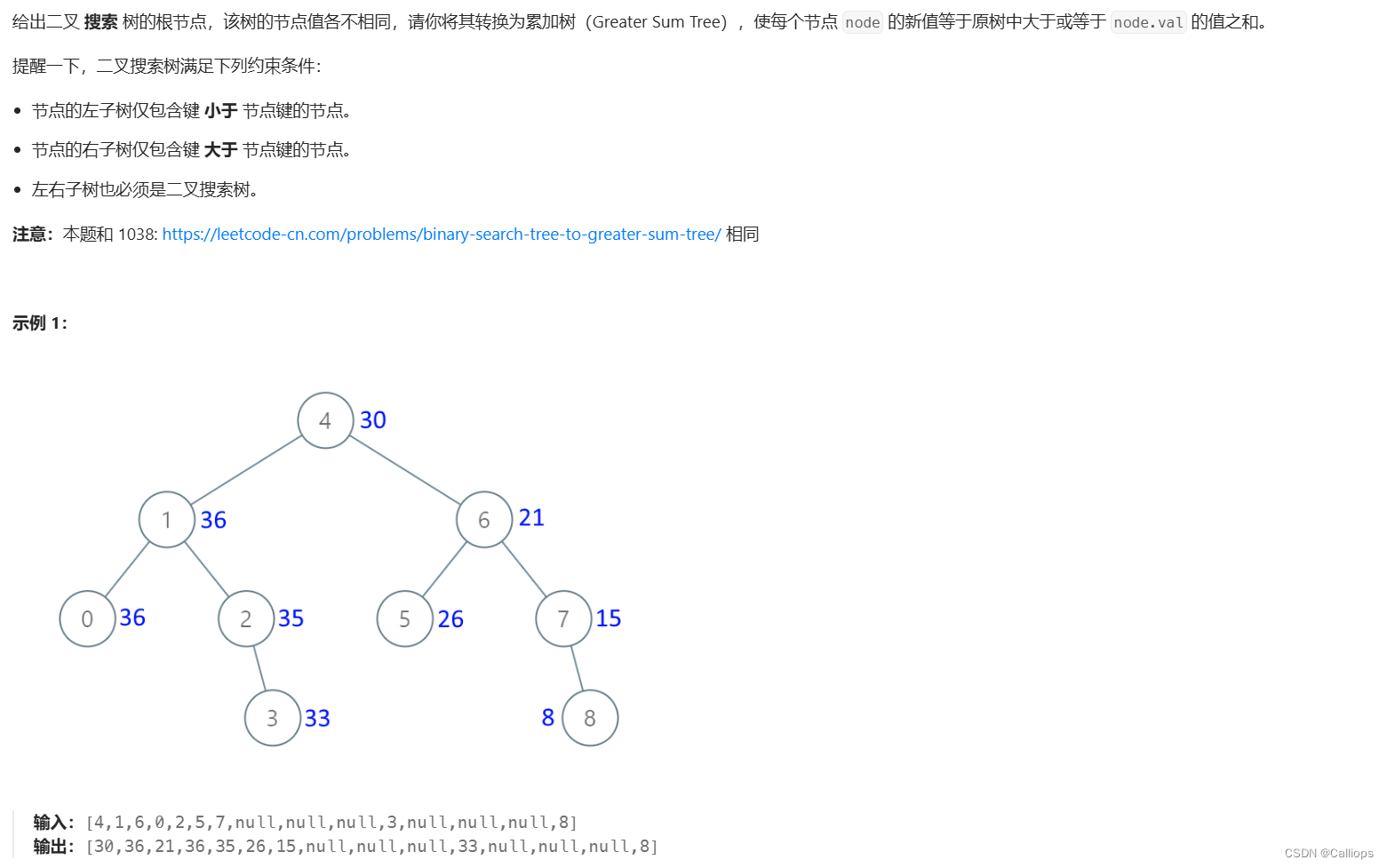
题目的意思是：将二叉树中某节点的新的值为原先树中大于这个节点的数的值的累加。

思路

总体思路：很简单，右中左遍历就行。定义一个全局变量累加

方法一

class Solution(object):
    def __init__(self):
        self.count = 0
        
    def traversal(self,root):
        if root == None: return None
        if root.right: self.traversal(root.right)
        self.count += root.val
        root.val = self.count
        if root.left: self.traversal(root.left)
        return root
    def convertBST(self, root):
        """
        :type root: TreeNode
        :rtype: TreeNode
        """
        re = self.traversal(root)
        return re
        

方法二

---

总结