解答02：Smith圆为什么能“上感下容 左串右并”？

在《解答01：Smith圆为什么能“上感下容 左串右并”？》中我们已经叙述反射系数的由来，进而对反射系数做归一化，再到归一化之后归一化阻抗在复平面的图形表示。接下来我们将开始尝试“掰弯”该图形，并且研究“掰弯”之后的特性——

生活中有很多将立体形状转化为平面形状的例子，

如将一个立体的橙子剥开并摊平，

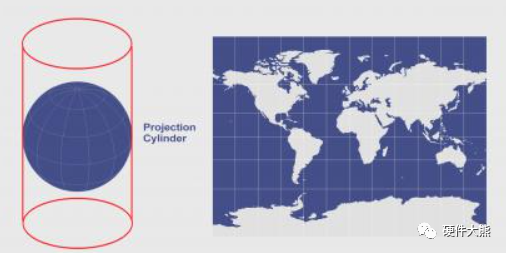
如将地图“掰弯”成为地球仪——

现在假设给你一个如下的臂力棒，

接下来，请你将该臂力棒“掰弯”——

复平面坐标与Smith圆图都是二维平面，将复平面图形中的线如同掰弯臂力棒一般操作，于是直线开始演化为曲线——

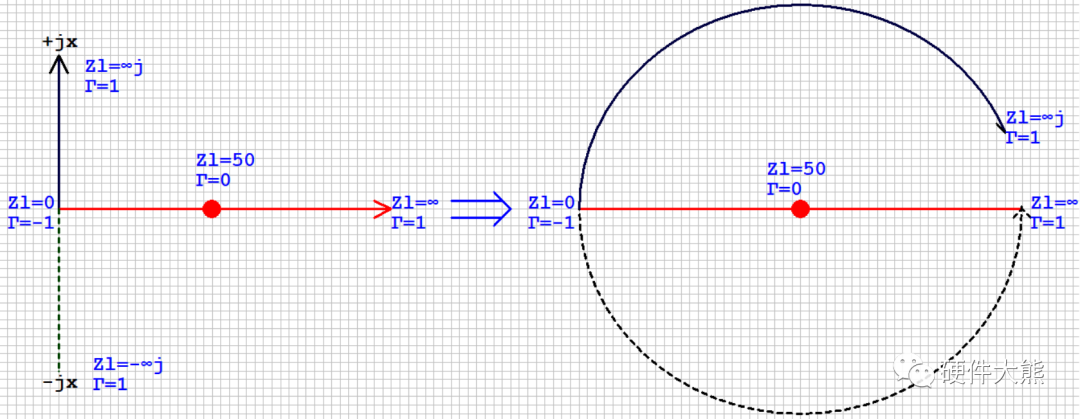
曲线演化成为闭合的圆线——

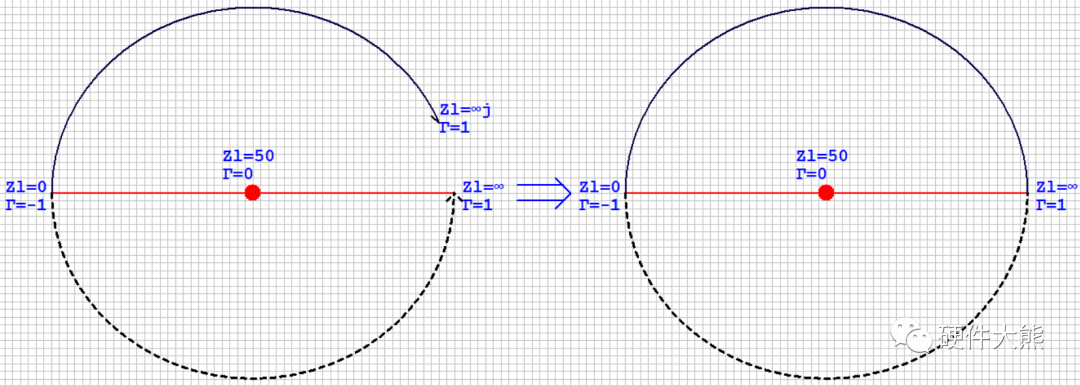
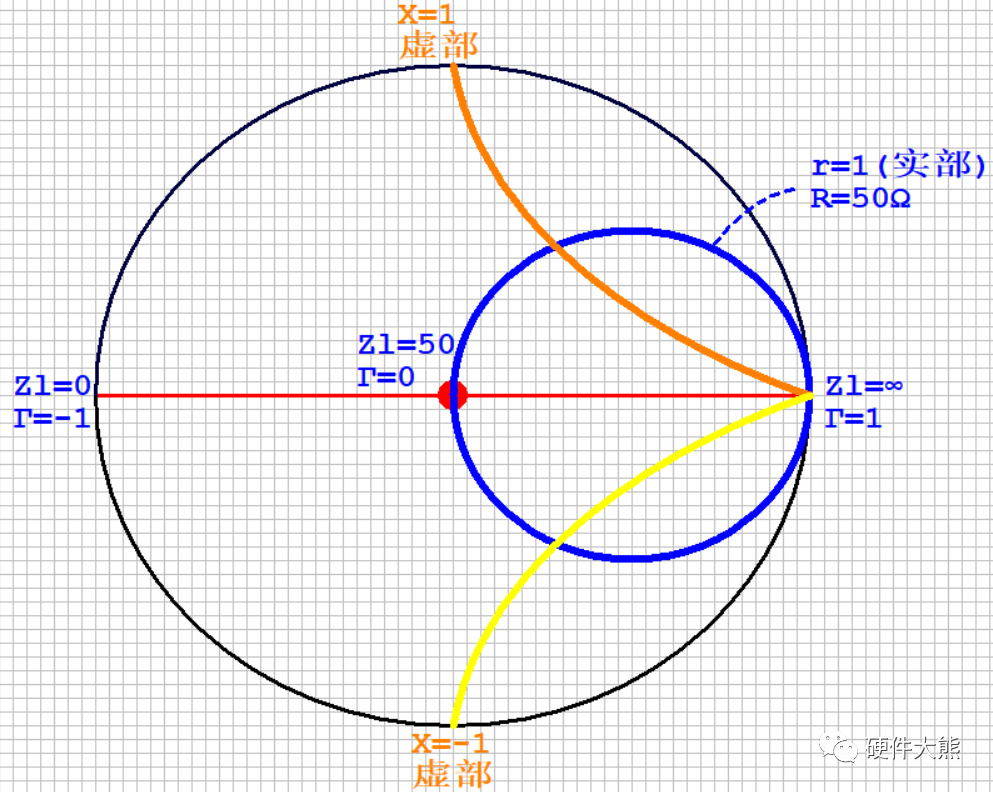
此时，我们已经将复平面的直角坐标图变化为Smith圆图，为了加深理解，有几条典型的线需要再了解下

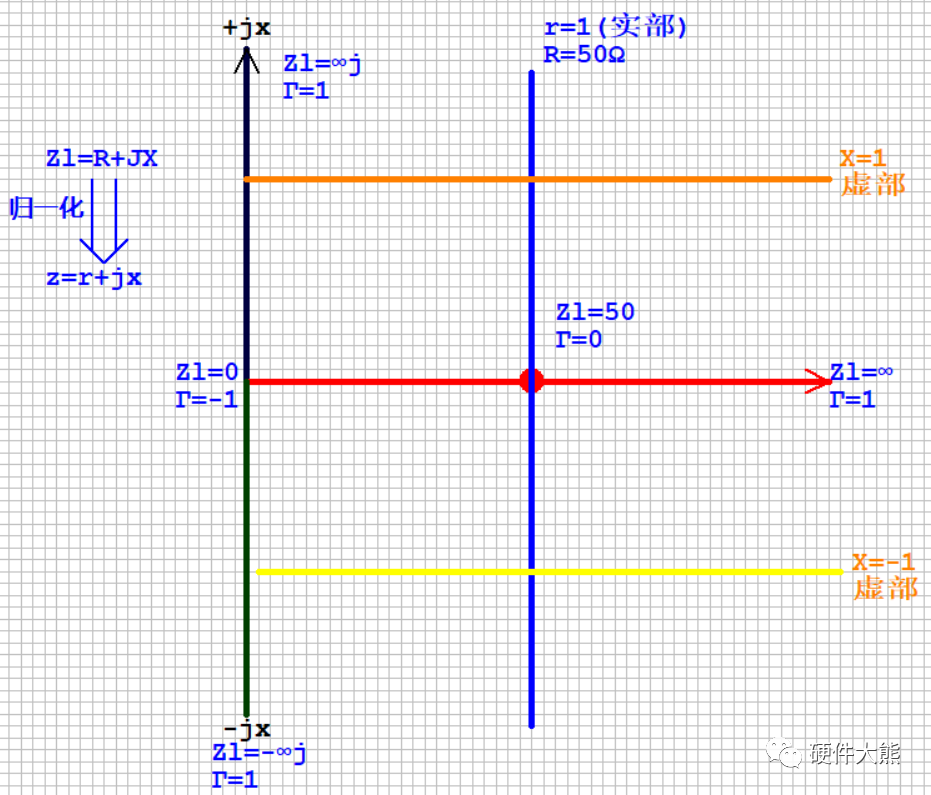
黑色的线上的阻抗，有个特点：实部为0；(电阻为0)

红色的线上的阻抗，有个特点：虚部为0；(电感、电容为0)

蓝色的线上的阻抗，有个特点：实部为1；(电阻为50欧姆)

黄色的线上的阻抗，有个特点：虚部为-1；

橙色的线上的阻抗，有个特点：虚部为1

转化为Smith圆图进行体现：

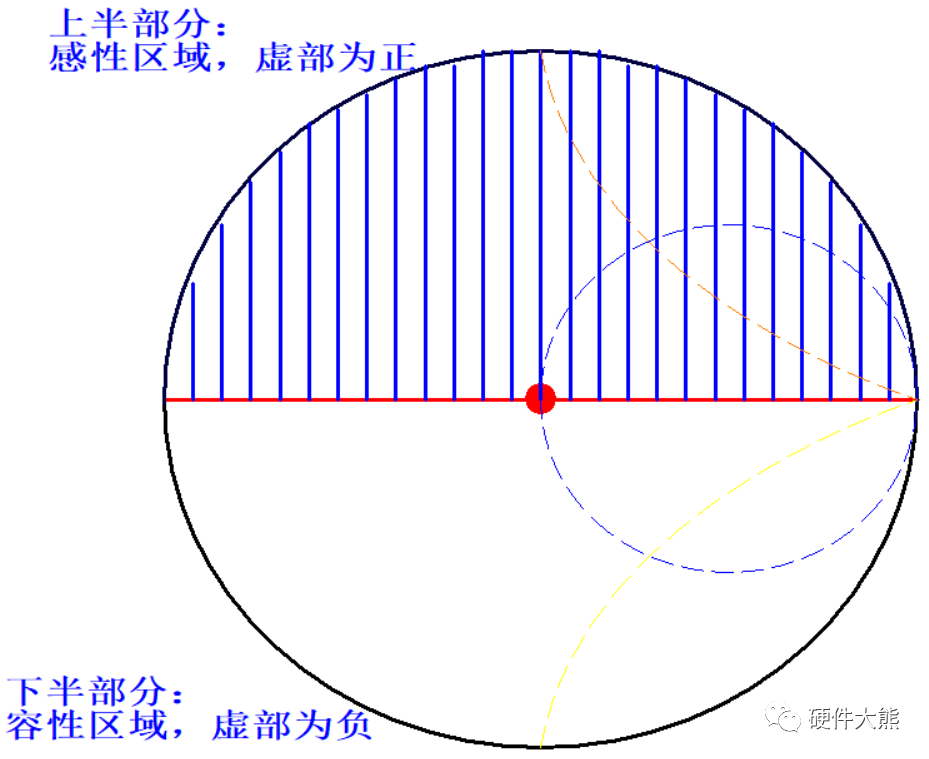
通过Smith圆图，除了特殊的线，我们还可以简单直观地观察部分区域，以如下两个为例：

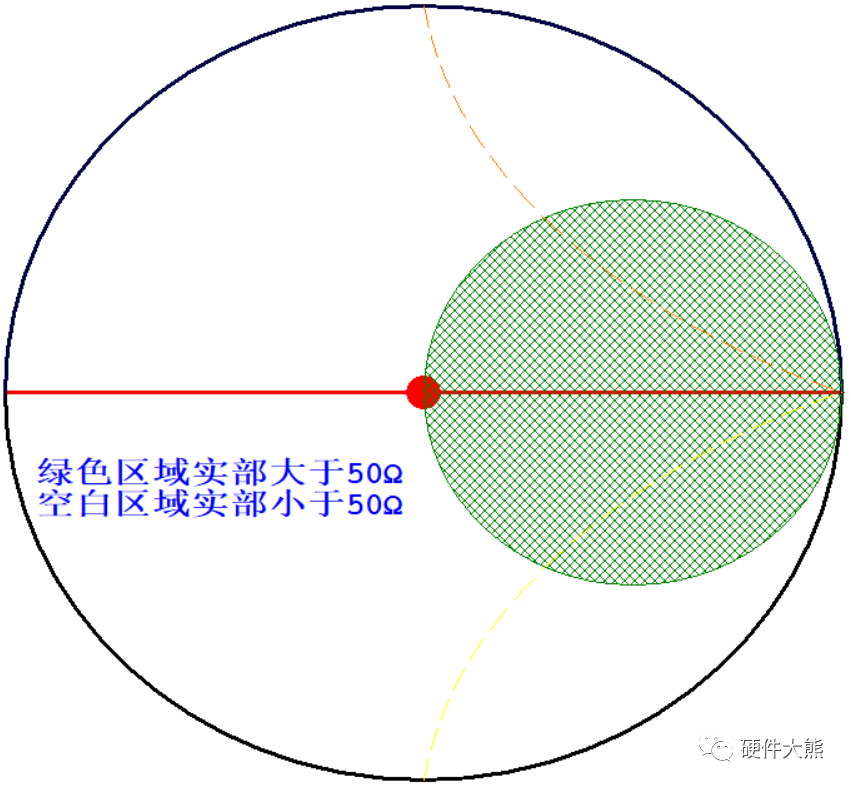
目前我们已经叙述了Smith圆图的形成过程，并且稍微了解了典型的特性曲线、区域，

关于“上感下容，左串右并”的问题还差一个门槛， 篇幅所限，留待下一个篇章进行叙述。

原创不易，若有转载需求，务必告知！

如果我的文字对你有所启发或帮助，

“点赞\转发”是对我最大的支持

推荐阅读：

硬件大熊原创合集(2021/12更新)