指标权重确定方法及具体步骤介绍？

客观的指标权重确立方法主要是根据原始数据之间的关系，来确定各指标权重，其原始数据来自于各指标在评价中的实际数据。

常用的客观赋权法包括变异系数法、熵值法、CRITIC法、回归分析和结构方程模型等等，下面我们来简单介绍一下回归分析法和结构方程模型：

回归分析

回归分析（Regeression Analysis）指的是确定两种或两种以上变量间相互依赖的定量关系的⼀种统计分析⽅法。它同样也可以被用来计算指标权重，具体方法如下：

1. 去除量纲，指标正向化处理
2. 建立回归模型，计算回归系数
3. 使用回归系数作为原始相对影响力系数
4. 影响力系数归⼀化处理： W(i)=X(i)/（X(1)+X(2) +X(3) +……+X(n)

这里要强调⼀下：去除量纲，是确定指标权重的第⼀步，也是最重要的⼀步。因为在实际研究中，不同的变量单位不同，数值差异极大，例如100g和1m，这样会给综合分析建模带来不便。因此，我们需要对收集得到的数据进行去量纲，即去掉单位对数值的影响，使所有的变量都在同等的水平上，才能“公平”地参与后续处理。

结构方程模型

结构方程模型（Structural Equation Modeling，简称SEM）是瑞典统计学家、心理测量学家Karl·G·Joreskog于20世纪70年代中期提出⼀种统计分析方法，主要用于探索变量之间的关系。那么，如何用它来计算指标权重呢？让我们用下图来举例说明：

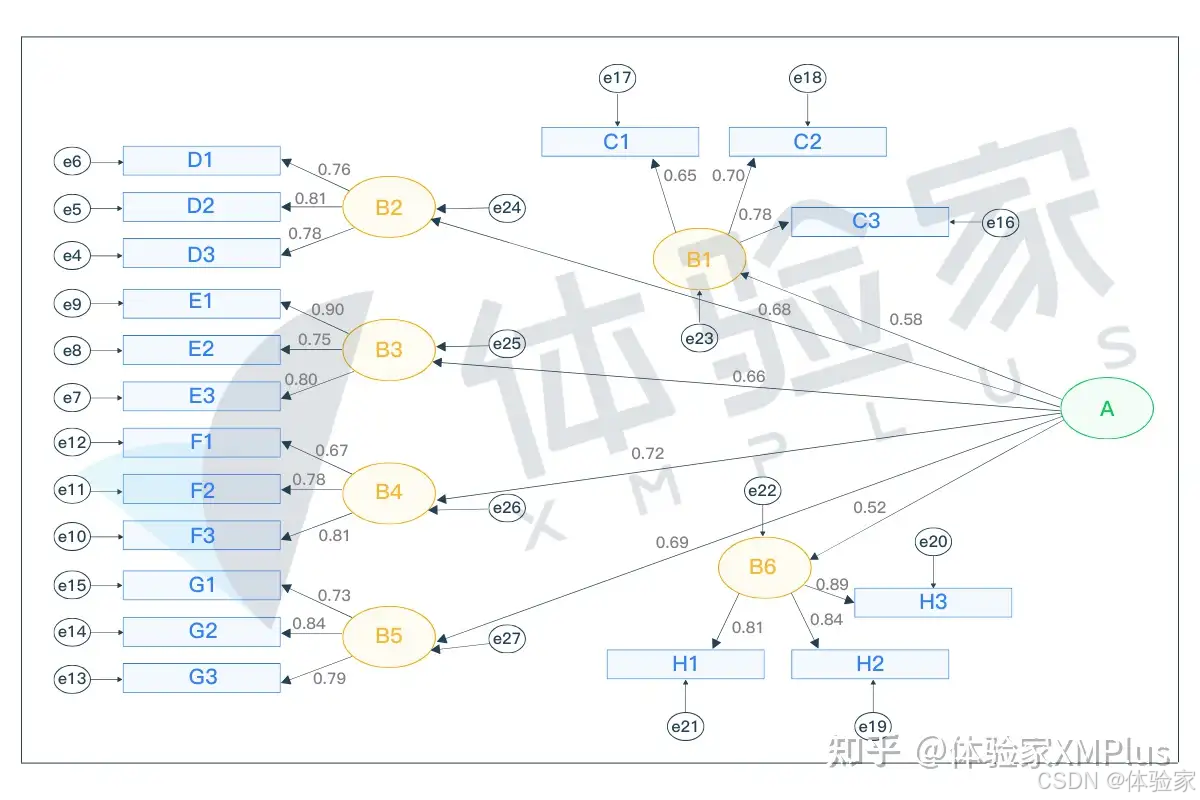
1.计算各三级指标的权重系数

如上图所示，A对应的6个⼆级指标（B1-B6），B分别对应的三级指标。以B1为 例 ， C1 的 权 重 系 数 =C1 的 因 子 负 荷 /C1-C3 的 因 子 负 荷 总 值 ， 即 C1=0.65/ （0.65+0.70+0.78）≈0.33，最终得出三级指标的权重，如下表：

2.计算各⼆级指标的权重系数

仍以B1为例，B1的权重系数=B1的因子负荷/B1-B6的因子负荷总值，即B1=0.58/ （0.58+0.68+0.66+0.72+0.69+0.52），最终得出⼆级指标的权重，如下表：