51Nod1262扔球

最新推荐文章于 2020-04-08 17:02:26 发布

原创最新推荐文章于 2020-04-08 17:02:26 发布 · 293 阅读

0 ·

CC 4.0 BY-SA版权

ACM 专栏收录该内容

11 篇文章

订阅专栏

探讨了在一个圆形路径上，球经过N次反弹返回起点而不提前经过该点的所有可能路径计数问题。利用欧拉函数计算方案数量，介绍了欧拉函数的计算方法及其在解决此类问题中的应用。

题目链接
在圆上一点S，扔出一个球，这个球经过N次反弹还有可能回到S点。N = 4时，有4种扔法，如图：
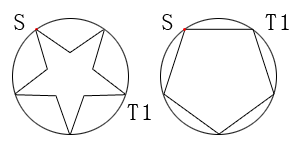
在这里插入图片描述
恰好经过4次反弹回到起点S（从S到T1，以及反向，共4种）。
给出一个数N，求有多少种不同的扔法，使得球恰好经过N次反弹，回到原点，并且在第N次反弹之前，球从未经过S点。

输入
输入一个数N(1 <= N <= 10^9)。
输出
输出方案数量。
题解：
先给出答案，为 n+1 的欧拉数。
n 次反弹，在园上形成等分成 n 段，共 n+1个等分点，按顺时针一次编号为 1, 2, 3, …, n+1, 显然这样总共就有 n 种方案，每种方案的每次反弹间距为 d 个等分距离，d 从1 到 n, 当 d 与 n+1 互质时才是正确的方案，否则就会在第 n 次反弹之前就已经达到 S 点。因此答案就是 $\varphi(n+1)$ 。
欧拉函数可以 $O\sqrt{n}$ 求解。

#include <bits/stdc++.h>
using namespace std;

int euler(int n){
    int ans = n;
    for(int i = 2; i * i <= n; i ++){
        if(n % i == 0){
	    ans = (ans / i) * (i - 1);
	    while(n % i == 0) n /= i;
	}
    }
    if(n > 1) ans = (ans / n) * (n - 1);
    return ans;

}

int main()
{
    int n; scanf("%d", &n);
    printf("%d\n", euler(n + 1));
    return 0;
}