基于树的数组 Array Based on Tree

已于 2024-12-17 11:07:39 修改
阅读量215 收藏
点赞数
分类专栏： 算法手册 文章标签： 数据结构 算法
于 2023-06-01 22:57:19 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/CQRuler/article/details/130997066
版权

        基于树的数组（Array Based on Tree，简称ABT），是一种基本数据结构，它是基于平衡二叉树的数组，并根据其左右子树的节点数来维持平衡。不同于二叉搜索树（Binary Search Tree），ABT维持的是元素的插入顺序而非节点的键值顺序。ABT不仅具备随机访问能力，而且具备动态编辑能力，其随机访问、插入和删除操作的时间复杂度均为O(log n) 。

适用场景

        数组（Array）和链表（List）是两种常见的数据结构。数组的随机访问时间复杂度为O(1)，而链表的插入和删除时间复杂度为O(1)。然而，有时我们需要一种数据结构，能够结合数组和链表的优点。因此，基于树的数组（Array Based on Tree）的概念应运而生。ABT很好地平衡了随机访问、插入和删除操作的性能，适用于同时需要随机访问与动态编辑的应用场景。

特性

        ABT是一种基于非排序二叉树的数据结构，具有以下特性：

        （1） 左子树节点数不小于其两个侄子所在子树的节点数。

        （2） 右子树节点数不小于其两个侄子所在子树的节点数。

        （3） 左右子树均为ABT。

        考虑以下示例，其中T是ABT的节点，L和R是其子节点，A、B、C和D是满足上述ABT特性的子树。

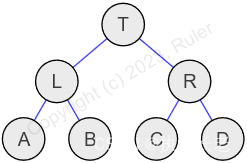
         根据ABT的特性，节点T必须满足：

        （1） size(L) >= max(size(C), size(D))

        （2） size(R) >= max(size(A), size(B))

节点

        ABT的节点包括一个父节点、两个子节点以及该节点所在子树中的节点数量。

         节点定义的C++代码如下：

// Class template abt_node
template <class T>
struct abt_node
{
	using node_type            = abt_node<T>;
	using node_pointer         = node_type*;
	using const_node_pointer   = const node_type*;
	using node_reference       = node_type&;
	using const_node_reference = const node_type&;

	node_pointer               parent;
	node_pointer               left;
	node_pointer               right;
	size_t                     size;
	T                          data;
};

旋转操作

        如同其他自平衡二叉树，当插入或删除节点导致大小平衡树失去平衡时，需要通过旋转操作来恢复平衡。

        常见的旋转操作包括左旋转和右旋转，这可以通过交换节点和子树的位置来实现。下面介绍左右旋转的操作过程。

左旋转

        左旋转用于使节点T的右子节点R成为其父节点，并使其右子节点R的左子节点A成为其右子节点。此操作使原节点T成为其右子节点R的左子节点，从而维持二叉树的平衡。

         左旋转的C++代码如下：

node_pointer rotate_left(node_pointer t)
{
	node_pointer r = t->right;
	t->right = r->left;
	if (r->left)
		r->left->parent = t;
	r->parent = t->parent;
	if (t == _head->parent)
		_head->parent = r;
	else if (t == t->parent->left)
		t->parent->left = r;
	else
		t->parent->right = r;
	r->left = t;
	r->size = t->size;
	t->parent = r;
	t->size = (t->left ? t->left->size : 0) + (t->right ? t->right->size : 0) + 1;
	return r;
}

右旋转

        右旋转与左旋转类似，但方向相反。右旋转用于使节点T的左子节点L成为其父节点，并使其左子节点L的右子节点B成为其左子节点。此操作使原节点T成为其左子节点L的右子节点，从而维持二叉树的平衡。

        右旋转的C++代码如下：

node_pointer rotate_right(node_pointer t)
{
	node_pointer l = t->left;
	t->left = l->right;
	if (l->right)
		l->right->parent = t;
	l->parent = t->parent;
	if (t == _head->parent)
		_head->parent = l;
	else if (t == t->parent->right)
		t->parent->right = l;
	else
		t->parent->left = l;
	l->right = t;
	l->size = t->size;
	t->parent = l;
	t->size = (t->left ? t->left->size : 0) + (t->right ? t->right->size : 0) + 1;
	return l;
}

重新平衡

        当对ABT进行插入或者删除操作后，可能违反ABT的特性，需要对以T为根的ABT进行重新平衡。再平衡的前提是T的子树均满足ABT的特性。重新平衡需要考虑以下4种情况：

        （1） size(T.left)<size(T.right.left)

        可能发生在节点T的右子树插入节点或者左子树删除节点后。先对T的右子节点R进行右旋转，再对T进行左旋转。此时，子树A、B、D、E、F 和 L 仍然满足 ABT的特性；而左子树T和右子树R可能违反ABT的特性。对于左子树T，由于其右子树的节点减少，可能出现size(T.right)<size(T.left.child)，需要重新平衡。对于右子树R，由于其左子树的节点减少，可能出现size(R.left)<size(R.right.child)，需要重新平衡。最后，对节点C及其祖先节点逐一进行重新平衡，直到根节点为止。

        （2） size(T.left) < size(T.right.right)

        可能发生在节点T的右子树插入节点或者左子树删除节点后。对节点T进行左旋转后，子树A、B、C、D、E、F、L仍然满足ABT的特性；而左子树T的右子树的节点减少，可能出现size(T.right)<size(T.left.child)，需要重新平衡。最后，对节点R及其祖先节点逐一进行重新平衡，直到根节点为止。

        （3） size(T.right) < size(T.left.right)

        可能发生在节点T的左子树插入节点或者右子树删除节点后。先对T的左子节点进行左旋转，再对T进行右旋转。此时，子树A、C、D、E、F、R仍然满足ABT的性质；而左子树L和右子树T可能违反ABT的特性。对于左子树L，由于其右子树的节点减少，可能出现size(L.right)<size(L.left.child)，需要重新平衡。对于右子树T，由于其左子树的节点减少，可能出现size(T.left)<size(T.right.child)，需要重新平衡。最后，对节点B及其祖先节点逐一进行重新平衡，直到根节点为止。

        （4） size(T.right)<size(T.left.left)

        可能发生在节点T的左子树插入节点或者右子树删除节点后。对节点T进行右旋转后，子树A、B、C、D、E、F、R仍然满足SBT的性质；而右子树T的左子树的节点减少，可能出现size(T.left)<size(T.right.child)，需要重新平衡。最后，对节点L及其祖先节点逐一进行重新平衡，直到根节点为止。

        向节点T的子节点插入节点后进行重新平衡的C++代码如下：

node_pointer insert_rebalance(node_pointer t, bool flag)
{
	if (flag)
	{
		if (t->right)
		{
			size_type left_size = t->left ? t->left->size : 0;
			// case 1: size(T.left) < size(T.right.left)
			if (t->right->left && left_size < t->right->left->size)
			{
				t->right = rotate_right(t->right);
				t = rotate_left(t);
				t->left = insert_rebalance(t->left, false);
				t->right = insert_rebalance(t->right, true);
				t = insert_rebalance(t, true);
			}
			// case 2. size(T.left) < size(T.right.right)
			else if (t->right->right && left_size < t->right->right->size)
			{
				t = rotate_left(t);
				t->left = insert_rebalance(t->left, false);
				t = insert_rebalance(t, true);
			}
		}
	}
	else
	{
		if (t->left)
		{
			size_type right_size = t->right ? t->right->size : 0;
			// case 3. size(T.right) < size(T.left.right)
			if (t->left->right && right_size < t->left->right->size)
			{
				t->left = rotate_left(t->left);
				t = rotate_right(t);
				t->left = insert_rebalance(t->left, false);
				t->right = insert_rebalance(t->right, true);
				t = insert_rebalance(t, false);
			}
			// case 4. size(T.right) < size(T.left.left)
			else if (t->left->left && right_size < t->left->left->size)
			{
				t = rotate_right(t);
				t->right = insert_rebalance(t->right, true);
				t = insert_rebalance(t, false);
			}
		}
	}
	return t;
}

        从节点T的子节点删除节点后进行重新平衡的C++代码如下：

node_pointer erase_rebalance(node_pointer t, bool flag)
{
	if (!flag)
	{
		if (t->right)
		{
			size_type left_size = t->left ? t->left->size : 0;
			// case 1: size(T.left) < size(T.right.left)
			if (t->right->left && left_size < t->right->left->size)
			{
				t->right = rotate_right(t->right);
				t = rotate_left(t);
				t->left = erase_rebalance(t->left, true);
				t->right = erase_rebalance(t->right, false);
				t = erase_rebalance(t, false);
			}
			// case 2. size(T.left) < size(T.right.right)
			else if (t->right->right && left_size < t->right->right->size)
			{
				t = rotate_left(t);
				t->left = erase_rebalance(t->left, true);
				t = erase_rebalance(t, false);
			}
		}
	}
	else
	{
		if (t->left)
		{
			size_type right_size = t->right ? t->right->size : 0;
			// case 3. size(T.right) < size(T.left.right)
			if (t->left->right && right_size < t->left->right->size)
			{
				t->left = rotate_left(t->left);
				t = rotate_right(t);
				t->left = erase_rebalance(t->left, true);
				t->right = erase_rebalance(t->right, false);
				t = erase_rebalance(t, true);
			}
			// case 4. size(T.right) < size(T.left.left)
			else if (t->left->left && right_size < t->left->left->size)
			{
				t = rotate_right(t);
				t->right = erase_rebalance(t->right, false);
				t = erase_rebalance(t, true);
			}
		}
	}
	return t;
}

插入操作

        如果ABT为空，则直接添加该节点作为根节点。否则，根据插入节点T的子节点的情况，可以分为以下两种情况：

        （1） 节点T没有左子节点

        在这种情况下直接插入到节点T的左子树中。其祖先节点的节点数应全部加1。可能出现上述第（3）种情况或者第（4）种情况，因此，节点T需要重新平衡。

        （2） 节点T已有左子节点

       在这种情况下选择其左子树中的最后一个节点作为实际插入节点X。插入到节点X的右子树中，其祖先节点的节点数应全部加1。可能会出现上述第（1）种情况或者第（2）种情况，因此，节点X需要重新平衡。

        插入操作的C++代码如下：

template <class ...Args>
node_pointer insert_node(node_pointer t, Args&&... args)
{
	// creates a new node
	node_pointer n = this->create_node(std::forward<Args>(args)...);
	n->left = nullptr;
	n->right = nullptr;
	n->size = 1;
	if (t == _head)
	{
		// if the tree is not empty
		if (_head->parent)
		{
			t = _head->right;
			// inserts the node
			n->parent = t;
			t->right = n;
			_head->right = n;
			// increases the size of nodes
			for (node_pointer p = t; p != _head; p = p->parent)
				++p->size;
			do
			{
				// rebalance after insertion
				t = insert_rebalance(t->parent, t == t->parent->right);
			} while (t->parent != _head);
		}
		else
		{
			// inserts the node
			n->parent = t;
			_head->parent = n;
			_head->left = n;
			_head->right = n;
		}
	}
	else if (t->left)
	{
		t = t->left;
		while (t->right)
			t = t->right;
		// inserts the node
		n->parent = t;
		t->right = n;
		// increases the size of nodes
		for (node_pointer p = t; p != _head; p = p->parent)
			++p->size;
		do
		{
			// rebalance after insertion
			t = insert_rebalance(t->parent, t == t->parent->right);
		} while (t->parent != _head);
	}
	else
	{
		// inserts the node
		n->parent = t;
		t->left = n;
		if (t == _head->left)
			_head->left = n;
		// increases the size of nodes
		for (node_pointer p = t; p != _head; p = p->parent)
			++p->size;
		do
		{
			// rebalance after insertion
			t = insert_rebalance(t->parent, t == t->parent->right);
		} while (t->parent != _head);
	}
	return n;
}

删除操作

        假设要删除的节点是T，根据节点T的子节点数量，可以分为以下两种情况：

        （1） 节点T最多有一个子节点

        在这种情况下，可以直接删除节点T。其祖先节点的节点数减少1。如果节点T具有子节点L或R，则用其子节点替换节点T。最后，重新平衡节点T的父节点。

        （2） 节点T有两个子节点

        在这种情况下，不能直接删除节点T，否则整个树将被破坏。当节点T的左子树L的节点数小于右子树R的节点数时，选择其右子树R中值最小的节点作为实际删除节点X；否则，选择其左子树L中值最大的节点作为实际删除节点X。然后交换节点T和节点X的位置，此时，与第（1）种情况完全相同。

         删除操作的C++代码如下：

void erase_node(node_pointer t)
{
	bool flag;
	node_pointer x;
	node_pointer parent;
	// if node t has two child nodes
	if (t->left && t->right)
	{
		if (t->left->size < t->right->size)
		{
			x = leftmost(t->right);
			// the rebalance flag
			flag = (x == x->parent->right);
			// reduces the size of nodes
			for (node_pointer p = x->parent; p != _head; p = p->parent)
				--p->size;
			// replaces node t with node x and removes node t
			t->left->parent = x;
			x->left = t->left;
			if (x != t->right)
			{
				x->parent->left = x->right;
				if (x->right)
					x->right->parent = x->parent;
				t->right->parent = x;
				x->right = t->right;
				parent = x->parent;
			}
			else
				parent = x;
			if (t == _head->parent)
				_head->parent = x;
			else if (t == t->parent->left)
				t->parent->left = x;
			else
				t->parent->right = x;
			x->parent = t->parent;
			x->size = t->size;
		}
		else
		{
			x = rightmost(t->left);
			// the rebalance flag
			flag = (x == x->parent->right);
			// reduces the size of nodes
			for (node_pointer p = x->parent; p != _head; p = p->parent)
				--p->size;
			// replaces node t with node x and removes node t
			t->right->parent = x;
			x->right = t->right;
			if (x != t->left)
			{
				x->parent->right = x->left;
				if (x->left)
					x->left->parent = x->parent;
				t->left->parent = x;
				x->left = t->left;
				parent = x->parent;
			}
			else
				parent = x;
			if (t == _head->parent)
				_head->parent = x;
			else if (t == t->parent->left)
				t->parent->left = x;
			else
				t->parent->right = x;
			x->parent = t->parent;
			x->size = t->size;
		}
		// rebalance after deletion
		node_pointer p = erase_rebalance(parent, flag);
		while (p != _head)
			p = erase_rebalance(p->parent, p == p->parent->right);
	}
	// if node t has one child node at most
	else
	{
		x = t->left ? t->left : t->right;
		// the rebalance flag
		flag = (t == t->parent->right);
		// removes node t
		if (x)
			x->parent = t->parent;
		if (t == _head->parent)
			_head->parent = x;
		else if (t == t->parent->left)
			t->parent->left = x;
		else
			t->parent->right = x;
		if (t == _head->left)
			_head->left = x ? leftmost(x) : t->parent;
		if (t == _head->right)
			_head->right = x ? rightmost(x) : t->parent;
		// reduces the size of nodes
		for (node_pointer p = t->parent; p != _head; p = p->parent)
			--p->size;
		if (t != _head)
		{
			// rebalance after deletion
			node_pointer p = erase_rebalance(t->parent, flag);
			while (p != _head)
				p = erase_rebalance(p->parent, p == p->parent->right);
		}
	}
	// destroy node
	this->destroy_node(t);
}

选择操作

        选择操作为ABT提供随机访问功能。

        选择操作的C++代码如下：

node_pointer select_node(size_type k)
{
	node_pointer t = header->parent;
	while (t)
	{
		size_type left_size = t->left ? t->left->size : 0;
		if (left_size < k)
		{
			t = t->right;
			k -= (left_size + 1);
		}
		else if (k < left_size)
			t = t->left;
		else
			return t;
	}
	return header;
}

代码下载

ab_tree 源代码-优快云博客icon-default.png?t=O83Ahttps://blog.youkuaiyun.com/CQRuler/article/details/144518592

在线学习的深度强化学习——Online Reinforcement Learning for Learning
AI天才研究院
09-01 3129
在人工智能和机器学习领域，深度强化学习（Deep Reinforcement Learning，DRL）已经成为一个备受关注的研究方向。传统的强化学习方法在处理高维状态空间和复杂决策问题时往往力不从心，而深度强化学习通过结合深度学习的强大表示能力，极大地扩展了强化学习的应用范围。然而，在实际应用中，我们常常面临着动态变化的环境和持续输入的数据流，这就要求学习算法能够实时地适应新的情况，不断调整和优化决策策略。在线学习（Online Learning）作为机器学习的一个重要分支，专门解决在。
基于密度的聚类（Density-based clustering）-- 核密度估计（kernel density estimation）
weixin_44746091的博客
06-29 3681
In density-based clustering, clusters are defined as areas of higher density than the remainder of the data set. Objects in sparse areas - that are required to separate clusters-are usually considered to be noise and border points. --wiki 在基于密度的聚类中，聚类定义为密度
ABT(Asynchronous Backtracking)多智能体异步回溯算法详解（附python代码：用ABT解决n皇后问题）
m0_50572808的博客
04-08 864
ABT(Asynchronous Backtracking)多智能体异步回溯算法原理和思路详解（附python代码：用ABT解决n皇后问题）
深入理解机器学习——基于决策树（Decision Tree）的模型：分类树和回归树
热门推荐
冯·诺依曼
09-17 31万+
决策树（Decision Tree）是一种基本的分类与回归方法。本文会讨论决策树中的分类树与回归树，后续文章会继续讨论决策树的Boosting和Bagging的相关方法。决策树由结点和有向边组成。结点有两种类型：内部结点和叶结点，其中内部结点表示一个特征或属性，叶结点表示一个类。 分类树 分类树是一种描述对实例进行分类的树形结构。 用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测...
Gossip 数据传输协议
baidu_39649815的博客
07-31 1万+
Hyperledger Fabric通过在交易执行（endorsement和committing）peer节点和交易ordering节点之间划分工作负载来优化块链网络性能，安全性和可扩展性。网络操作的这种解耦需要一个安全，可信的和可扩展的数据传播协议，以确保数据的完整性和一致性。为了满足这些要求，Hyperledger Fabric实现了Gossip数据传播协议。Gossip协议Peer利用goss
基于树结构的机器学习模型
Flyingzhan的博客
11-10 2229
基于树结构的机器学习模型 在深度学习被广泛应用之前，基于树形结构的机器学习模型，比如说决策树，随机森林，GBDT，Xgboost等等被广泛的应用到分类等常见场景中，下面总结一下常见一个一些树形结构的机器学习模型。 1：决策树 常见的决策树算法有ID3，C4.5，CART(classification and regression tree)等等。由于存在很多好的文章已经详细的介绍了这些算法，...
统计学习（七）：基于树的方法
qq_52737544的博客
05-23 1235
本文主要介绍了决策树的基本原理；装袋法、随机森林、提升法等内容
基于数组前缀树的高效频繁项集挖掘算法优化
本文主要探讨了一种名为"基于数组前缀树的频繁项集挖掘算法"（Algorithm of Frequent Itemsets Mining Based on Array Prefix-trees，简称AFP-Growth），该算法是针对数据挖掘领域中一项关键任务——频繁模式和频繁...
记录基于Vue.js的移动端Tree树形组件
Mr.小灰狼_随笔
06-09 1万+
Vue 树形选择器（ Vue tree select ）组件在搭建 Vue 的 app 中特别常用，Vue tree select 除了简单的树形结构外，还有非常多样的功能来配合不同场景的使用。比如搜索过滤，前端添加删除树枝，前端编辑修改子树名，拖拽排序，对用户操作事件记录等。本文记录了我自己使用多年最好用的 2款 Vue tree select 组件，每一款都经过我实际测试，推荐给大家。
Linux内核源码分析-基树处理- radix_tree
魏峰海的专栏
11-10 6756
Linux内核源码分析-基树处理- radix_tree本文主要参考《深入理解Linux内核》，结合2.6.11版的内核代码，分析内核文件子系统中的radix_tree处理函数。 注意： 1、 不描述内核同步、错误处理、参数合法性验证相关的内容 2、 源码摘自Linux内核2.6.11 stable版，获取命令: git clone git://git.kernel.org/pub/s
第10章－基于树的方法(1)-生成树
tongweiganglp的博客
05-05 3830
原文参考：https://onlinecourses.science.psu.edu/stat857/node/22 一，本章简介 1，本章主要学习目标 理解决策树的基本概念 理解构成决策树的三个基本元素 理解’不纯度’及其他度量公式的定义 知道如何估计每个树节点的各个所属分类的后验概率 理解基于树的分类方法的优点 理解训练误差(或称再代入误差) 和 代价复杂度测量方法，知道它们的区别，以
场景树和空间图
深入思考
02-06 5788
场景树 这是整个场景的一个层次结构的表示，通过一棵简单的树来实现：一个“节点”有一个父亲和任意数量的孩子。这个数据结构用来管理层次结构的物体变换（位置和方向），以及他们的动画。 在FlExtEngine中，CSceneNode类拥有一个update方法，用于对node的变换进行更新；它还有一个accept方法，这样就可以使用访问者模式以实现更好的扩展性。 空间图 这是整个场景的一个空间关系
【项目评级】ArcBlock（ABT）-区块链基石网络
hack289099734的博客
01-07 4360
报告主旨 鉴于中国国内投资者缺乏相应的区块链项目资料，数字世界团队整理了全球已经完成的、正在进行的，以及宣布未来将区块链的项目评测资料，以标准化的评级报告形式呈现在国内加密数字货币投资者眼前，以便于能直观的了解区块链项目的相关信息。 1项目市场（权重40%，实得分86分） 项目简述：ArcBlock（ABT）是全球第一个专注与开发和部署去中心化应用的区块链服务平台和生
三种基本的GC算法基石
pf1234321的专栏
06-04 804
一、 标记／清除算法内存中的对象构成一棵树，当有效的内存被耗尽的时候，程序就会停止，做两件事，第一：标记，标记从树根可达的对象（途中水红色），第二：清除（清楚不可达的对象）。标记清除的时候有停止程序运行，如果不停止，此时如果存在新产生的对象，这个对象是树根可达的，但是没有被标记（标记已经完成了），会清除掉。缺点：递归效率低性能低；释放空间不连续容易导致内存碎片；会停止整个程序运行；二、 复制算法把...
【数据结构】顺序表
2401_85487070的博客
04-27 295
本文是小编巩固自身而作，如有错误，欢迎指出！
List 的介绍 [数据结构 初阶]
zjt_2002的博客
04-27 186
本文主要介绍了 List 以及它的常用接口的介绍
【数据结构_堆
2401_87711435的博客
04-27 295
我说此刻最好
《代码整洁之道》第6章 对象和数据结构 - 笔记
最新发布
CoFFee________的博客
04-27 197
对象应该隐藏它的内部数据，只暴露可以操作这些数据的“行为”（也就是方法/函数）。你创建一个“用户”对象，这个对象内部可能存着用户的姓名、年龄、地址等数据。但在好的面向对象设计里，你不应该让外部代码直接去随意修改这些数据（比如user.name = "新的名字";相反，你应该给“用户”对象提供一些方法，比如user.setName("新的名字");或。在这些方法里面，你可以控制数据的有效性（比如检查年龄不能是负数），或者做一些附带的操作（比如修改姓名时记录日志）。
数据结构强化篇
m0_62119368的博客
04-27 294
每次从未排序的记录中选取最小关键字的记录，通过交换位置，加入已排序记录的末尾。因此，快排的速度与递归搜索树的高度息息相关。快排的时间复杂度为 ：n*递归深度。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值