【代码超详解】LightOJ 1197 Help Hanzo（区间质数筛法）

最新推荐文章于 2020-07-15 15:50:24 发布

原创最新推荐文章于 2020-07-15 15:50:24 发布 · 428 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#详解

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

本文深入探讨了求解特定区间内质数的有效算法——区间筛法，对比埃氏筛和欧拉筛，阐述了其原理及优化策略，提供了一份通过实际竞赛验证的AC代码示例。

一、题目描述

在这里插入图片描述

二、算法分析说明与代码编写指导

对于求指定区间 [a, b] 的质数的题目，通常 a 和 b 都比较大，而 b - a 不太大。
采用埃氏筛或者欧拉筛的代码，一般都会同时给出前若干个质数。如果有 m 个不超过 n 的数要判断是否为质数，最坏情况下的时间复杂度为
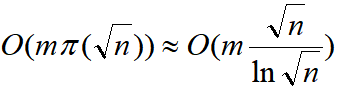
在这里插入图片描述
π(n) 为不大于 n 正整数中的质数数量。
在本例中，可以代入最坏情况 m = 100001，n = 2^31，得数据规模约为 4.3e+8。
当然，有很多数会在用很小的质数试除的时候就发现可以整除，从而被直接筛掉，不用再继续使用更大的质数试除。例如扣除仅用2、3、5、7、11、13、17、19 中的一个或几个质数就能筛掉的数，就足以使该规模大大减小。只是，这样的程度还不够。如果直接用这样的算法对每个区间的数进行逐个判断（最多有 200 组数据），还是会超时。
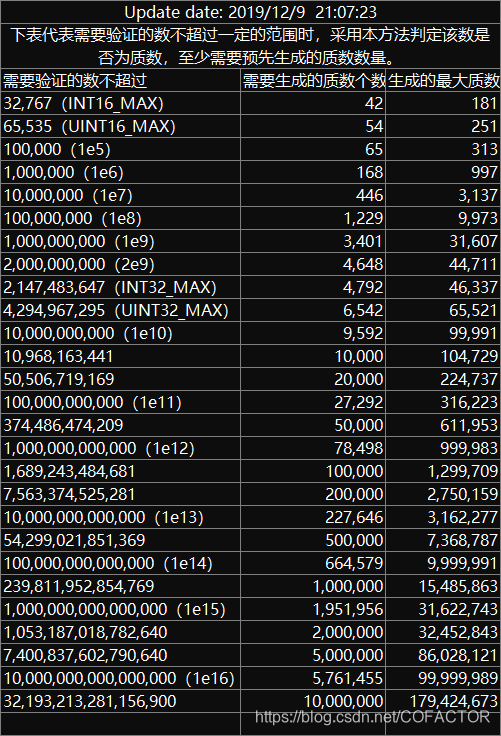
下面我们介绍区间筛法。本题中，由于区间的右端点 b 不超过 2^31 - 1，区间长度不超过 1e5 + 1，而判定 2^31 - 1 以内的质数，查表得至少需要打前 4792 个质数，打表范围内的最大质数为 46337。
在这里插入图片描述
然而，提交以后返回 Runtime Error，原因尚不明确。因此最终给出的 AC 代码中，数组开得大一些。
能不能用欧拉筛法直接打表直到区间右端点然后 O(1) 判断区间内的数呢？也是不可以的，因为打表范围还是太大了。
所以我们只能打表到根号b 的位置，然后技巧性地判断区间内的数到底是不是质数。不过，不可以用欧拉筛直接判断，因为欧拉筛法筛去合数必须严格地从 1 开始向后递推，而不能跳过中间的任何区间直接判断更大的数。所以我们需要采用埃氏筛法，在区间内一个一个筛去试除质数的倍数。
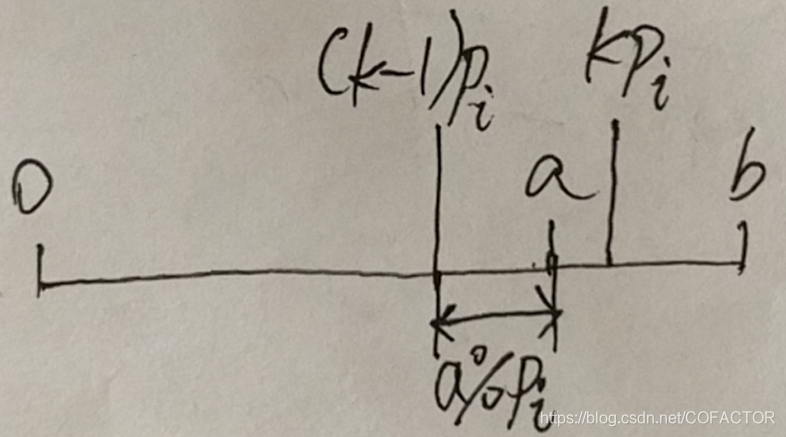
设一个 bitset iscompo 代表区间内的数是否为合数。k = max(2 * *J, *J * (a % *J != 0) + a / *J * *J) 的含义是：决定区间内开始标记合数的起点。如果 a 不能被正在试除的质数 *J 整除，那么起点是 *J × a / *J × *J。如果 a 能够被正在试除的质数 *J 整除，那么如果直接 *J + a / *J * *J，标记就会从 *J 的 (a + 1) 倍开始，而漏掉 a 倍 *J，所以在 a % *J = 0 的时候要补上 a 本身的标记。
不过如果仅仅这样处理，可能导致 a < *J 时，*J 本身在区间内从而被标记。质数的 1 倍（本身）是不可以标记的，必须从两倍开始标记，所以限制 k 最少要为 2 × *J。
特判：如果 a ≤ 1，可以发现 1 不会被标记为合数。而 1 本身也不是质数，因此要从总数中扣除。
在这里插入图片描述

三、AC 代码（144 ms）

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<bitset>
#pragma warning(disable:4996)
using namespace std;
//unsigned prime[4792], _PrimeTy, MaxPrime, * prime_end = prime; bitset<46338> notprime; bitset<100001> iscompo;
unsigned prime[8192], _PrimeTy, MaxPrime, * prime_end = prime; bitset<65536> notprime; bitset<131072> iscompo;
inline void gen_prime() {
	decltype(_PrimeTy) n = notprime.size() - 1, m = n / 2, L; notprime[0] = notprime[1] = true;
	for (decltype(_PrimeTy) i = 2; i <= m; ++i) {
		if (!notprime[i]) { *prime_end = i, ++prime_end; }
		L = n / i;
		for (auto j = prime; j != prime_end && *j <= L; ++j) {
			notprime[i * *j] = true; if (i % *j == 0)break;
		}
	}
	for (decltype(_PrimeTy) i = m + 1; i <= n; ++i)
		if (!notprime[i]) { *prime_end = i, ++prime_end; }
	MaxPrime = *(prime_end - 1);
}
unsigned T, a, b, c, t, l;
int main() {
	gen_prime();
	scanf("%u", &T);
	for (unsigned i = 1; i <= T; ++i) {
		scanf("%u%u", &a, &b); c = 0; l = b - a + 1; t = sqrt(b); iscompo.reset();
		for (auto J = prime; *J <= t; ++J) {
			for (auto k = max(2 * *J, *J * (a % *J != 0) + a / *J * *J); k <= b; k += *J) {
				iscompo[k - a] = 1;
			}
		}
		for (unsigned i = 0; i < l; ++i)if (!iscompo[i])++c;
		if (a == 1)--c;
		printf("Case %u: %u\n", i, c);
	}
	return 0;
}