lbm格子玻尔兹曼方法mrt模拟加热气泡脱离c++代码

LBM格子玻尔兹曼方法与MRT模拟加热气泡脱离的C++代码实现

一、引言

LBM（Lattice Boltzmann Method）格子玻尔兹曼方法是一种计算流体动力学的数值方法，特别适用于模拟复杂流体流动和界面现象。MRT（Multiple Relaxation Time）是LBM的一种改进算法，它通过引入多个松弛时间来更好地模拟复杂的流动情况。本文将介绍如何使用LBM格子玻尔兹曼方法和MRT算法来模拟加热气泡的脱离过程，并给出相应的C++代码实现。

二、LBM格子玻尔兹曼方法和MRT算法简介

LBM是一种基于粒子方法的流体动力学模拟方法，通过模拟流体中粒子的运动来求解流体动力学方程。MRT算法是LBM的一种改进算法，通过引入多个松弛时间来提高算法的稳定性和精度。在MRT算法中，每个格子上的分布函数被分解为多个部分，每个部分对应一个松弛时间，从而更好地模拟复杂的流动情况。

三、模拟加热气泡脱离的C++代码实现

下面是一个简单的C++代码实现，用于模拟加热气泡的脱离过程。代码主要包含以下几个部分：初始化、LBM格子玻尔兹曼方法、MRT算法和边界处理。

1. 初始化部分：设置仿真参数、格子大小、时间步长等。
2. LBM格子玻尔兹曼方法：根据流体动力学方程，计算每个格子上的分布函数。
3. MRT算法：将每个格子上的分布函数分解为多个部分，并分别设置不同的松弛时间。通过迭代求解，得到新的分布函数。
4. 边界处理：根据不同边界条件（如壁面、气泡等），对边界处的格子进行处理。

以下是部分代码示例：

// 初始化部分
int latticeSize = ...; // 格子大小
double timeStep = ...; // 时间步长
// ... 其他初始化参数 ...

// LBM格子玻尔兹曼方法
void lbm() {
    // 计算每个格子上的分布函数...
}

// MRT算法
void mrt() {
    // 将每个格子上的分布函数分解为多个部分...
    // 设置不同的松弛时间...
    // 通过迭代求解，得到新的分布函数...
}

// 边界处理
void boundaryTreatment() {
    // 根据不同边界条件进行处理...
}

int main() {
    // 初始化部分...
    while (simulationTime < totalTime) { // 循环执行仿真过程，直到达到总时间
        lbm(); // 执行LBM格子玻尔兹曼方法...
        mrt(); // 执行MRT算法...
        boundaryTreatment(); // 处理边界条件...
        // ... 其他仿真过程 ...
        simulationTime += timeStep; // 更新仿真时间...
    }
}

四、结论

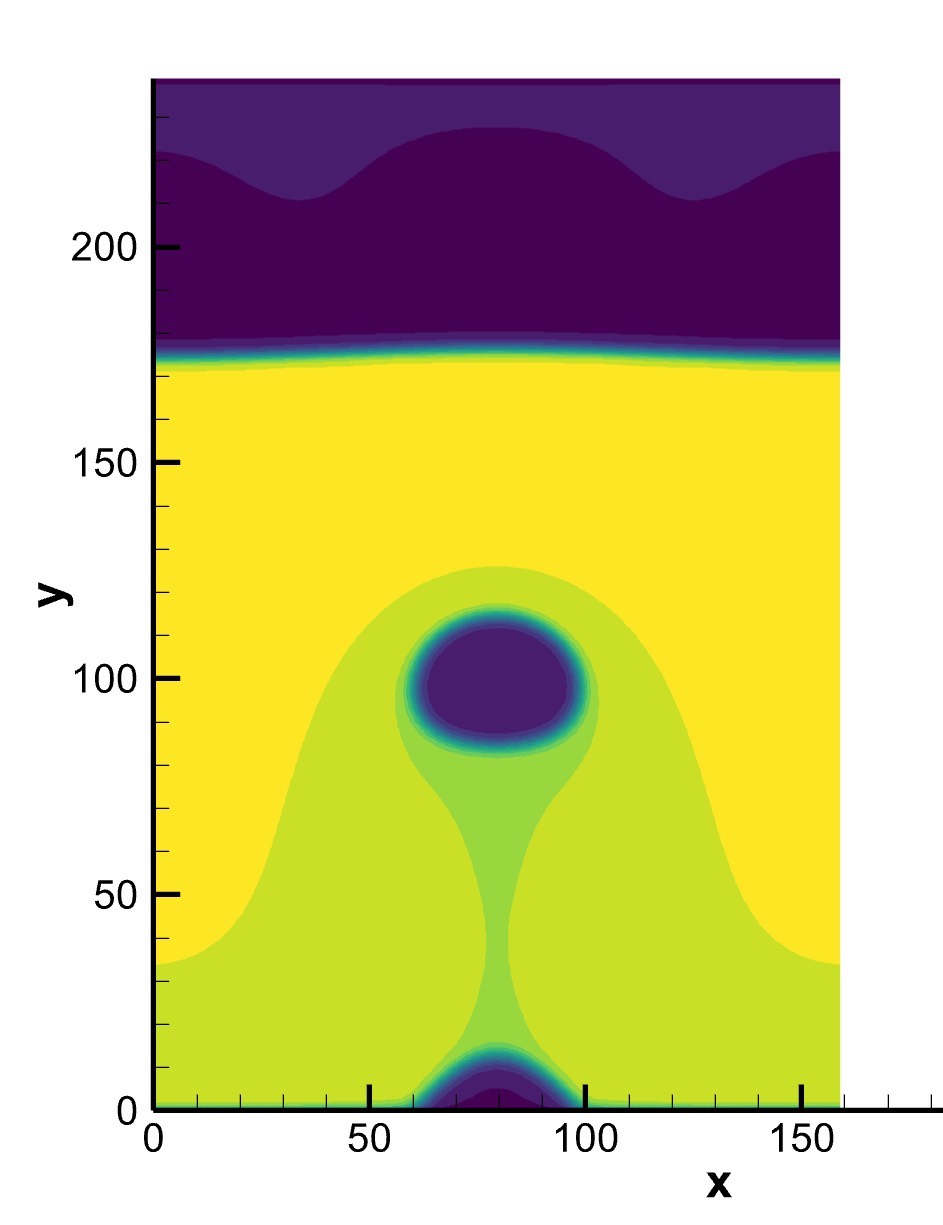
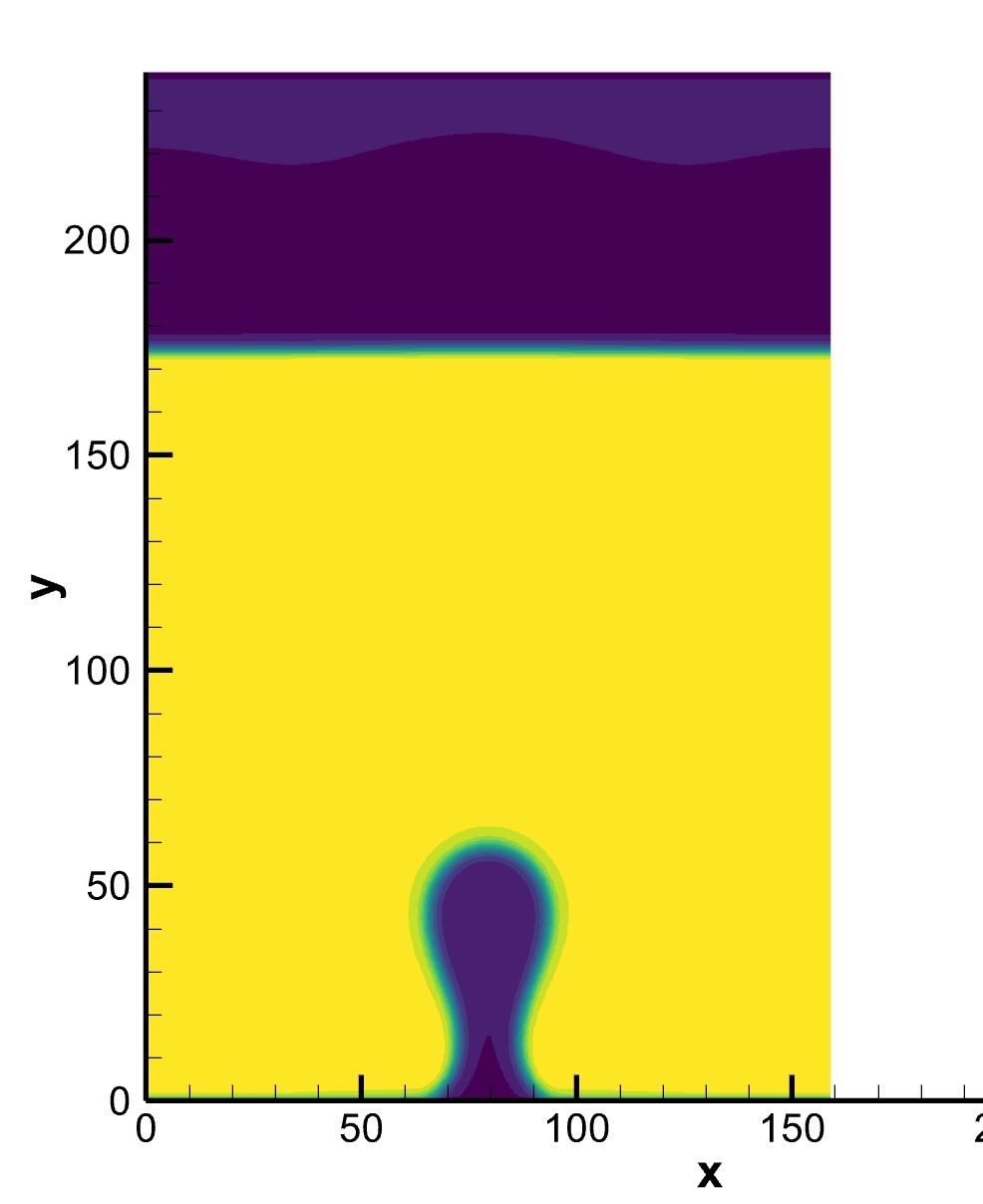
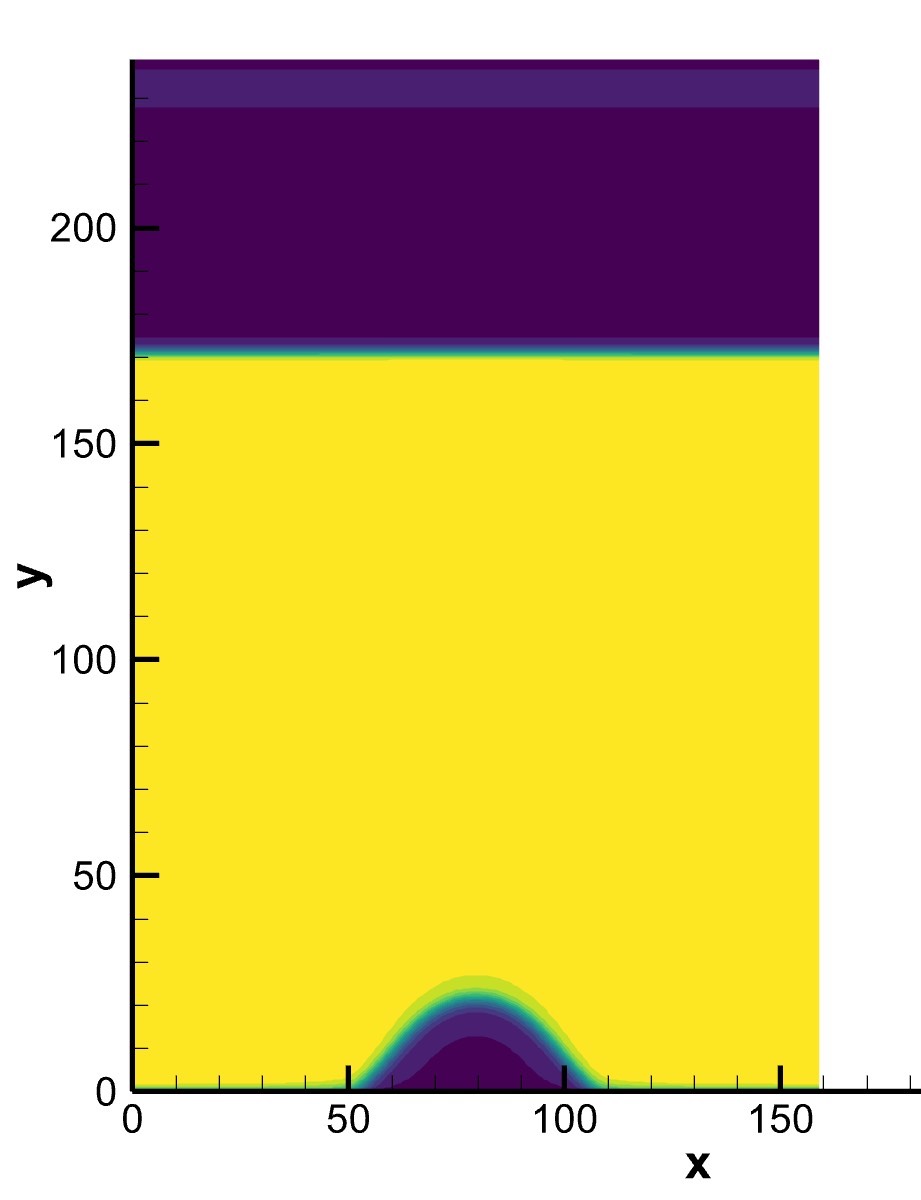
本文介绍了LBM格子玻尔兹曼方法和MRT算法在模拟加热气泡脱离过程中的应用，并给出了相应的C++代码实现。通过不断优化和调整参数，可以得到更准确的模拟结果。这种方法可以用于研究复杂流体流动和界面现象，具有广泛的应用前景。
lbm格子玻尔兹曼方法mrt模拟加热气泡脱离c++代码