5960 差分约束系统

5960 差分约束系统

这个知识点，一直都不会，但是听说过，直到练习完最短路，就顺带学习一下，原来就是给定一些形如x-y<=b的不等式的约束，问是否有解
这个问题和图论有什么关系？
不过这个这个知识点还真能转换成图论中的最短路问题
比如我们给出三个不等式，b-a<=k1，c-b<=k2，c-a<=k3c，求出c-a的最大值，我们来把这a，b，c转换成三个点，然后，k1，k2，k3表示权值
如图：

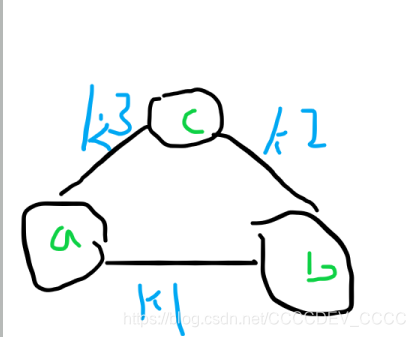
由题目我们可以知道，在这个图中，b-a<=k1，c-b<=k2，得出c-a<=k1+k2，这样我们就能比较k1+k2和k3的大小，求出c-a的最大值
然后根据我说的这个，我们大概就能猜到求解过程实际就是求a到c的最短路径，简单的说就是从a到c沿着某条路径后把所有权值求出和k求出，c-a<=k
所以我们根据这个来求最短路径，就很简单了
当然，题目题目绝对不会这么模板，我们需要根据题目学会变形

#include <stdio.h>
#include <bits/stdc++.h>

using namespace std;

int n, m, cnt, elast[5005], dis[5005], num[5005];
bool vis[5005];

struct edge {
	int to, len, next;
} e[10005];

queue<int> q;

void add (int u, int v, int w) {//邻接表存图
	e[++cnt].to = v;
	e[cnt].len = w;
	e[cnt].next = elast[u];
	elast[u] = cnt;
}

bool spfa (int x) {
	dis[x] = 0;
	q.push(x);
	vis[x] = true;
	num[x]++;
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		vis[u] = false;
		for (int i = elast[u]; i != 0; i = e[i].next)
			if (dis[e[i].to] > dis[u] + e[i].len) {
				dis[e[i].to] = dis[u] + e[i].len;
				if(!vis[e[i].to]) {
					q.push(e[i].to);
					vis[e[i].to] = true;
					num[e[i].to]++;
					if(num[e[i].to] == n + 1) return false;
				}
			}
	}
	return true;
}

int main() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++)
		dis[i] = INT_MAX;//初始无穷大
	for (int i = 1; i <= m; i++) {
		int u, v, w;
		scanf("%d %d %d", &u, &v, &w);
		add(v, u, w);
	}
	for (int i = 1; i <= n; i++)
		add(n + 1, i, 0);
	if (!spfa(n + 1)) {
		printf("NO");
		return 0;
	}
	for (int i = 1; i <= n; i++)
		printf("%d ", dis[i]);
	return 0;
}

好了，去做题去吧…