python训练营打卡DAY12

@浙大疏锦行

贝叶斯优化可视化和随机森林的解读

一、元组类型

为了学习今天的内容，我们学习一下最后一个没提的基本数据类型，元组（tuple）具有以下特点：

1. 有序：可以通过索引取出来元素
2. 不可变，不可修改
3. 可迭代、可切片 所以元组适合存储不应被程序意外修改的数据（例如配置常量、数据库记录的字段等）。函数返回多个值时，默认就是以元组的形式返回的。由于元组是不可变的，它可以作为字典的键（List 不可以）。

你也会发现元组和字符串性质一样啊，那为什么需要2个数据结构来表达这两个类型么，是因为它们之间的根本区别在于它们内部存储的元素类型

• 元组可以存储任意不同类型的数据对象（异构）。例如：整数、浮点数、列表、函数等。----异构容器，类似于表格存储
• 字符串只能存储字符（本质上是文本数据，都是字符类型）。---同构序列，文件名存储

不可变意味着他不具备增删改的步骤，增加就是创建新元组了

先看下创建元组的方法

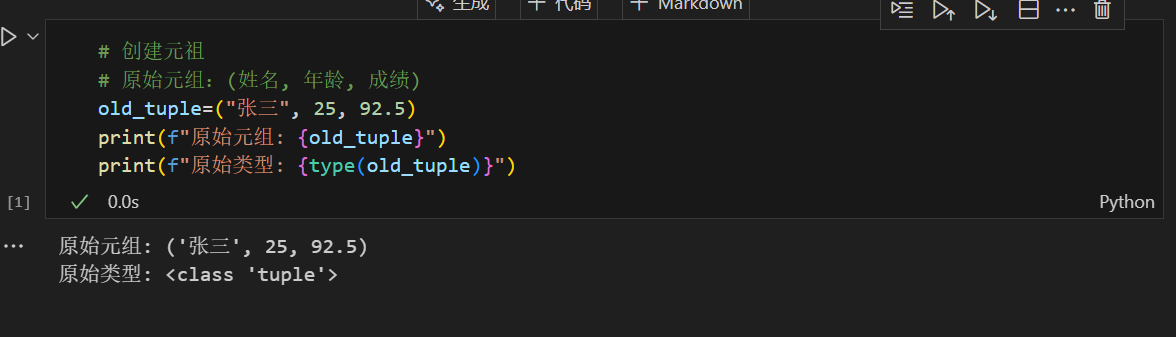
修改元组的方法

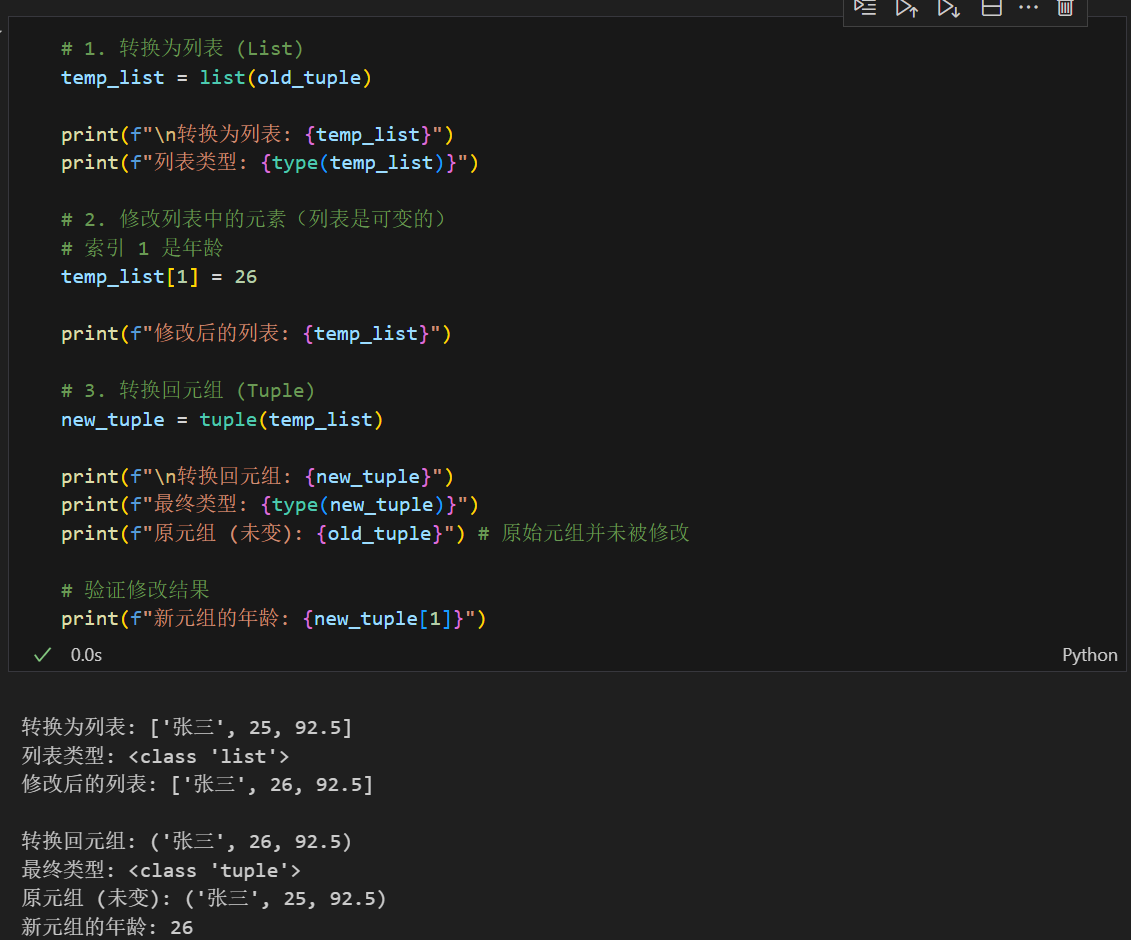
二、字典的items方法

字典的items方法，这个方法很重要，在后面深度学习的代码中自由度很高，我们会频繁接触到这个方法，我们来介绍下

items() 方法是 Python 中 字典 (Dictionary) 对象的一个非常常用的方法。它返回一个由字典中所有 (键, 值) 对 组成的视图对象（View Object）。这个视图对象可以用于迭代字典中的所有键值对。本质这也是python的解包操作的一种，我们后续会有专题重点讲解下解包操作。

什么叫视图对象？具有视图特性，返回的对象是动态的。如果原始字典在您获取 items() 视图后发生了变化（例如添加或删除了键值对），视图对象也会实时反映这些变化。

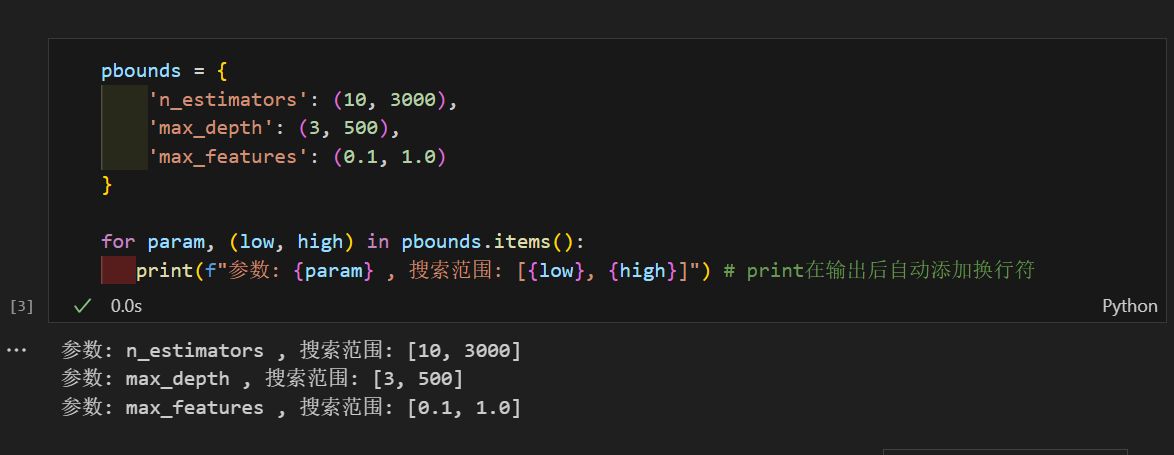
这和我们前几天说的enumerate方法非常像，他可以遍历任何可迭代对象，返回索引+元素

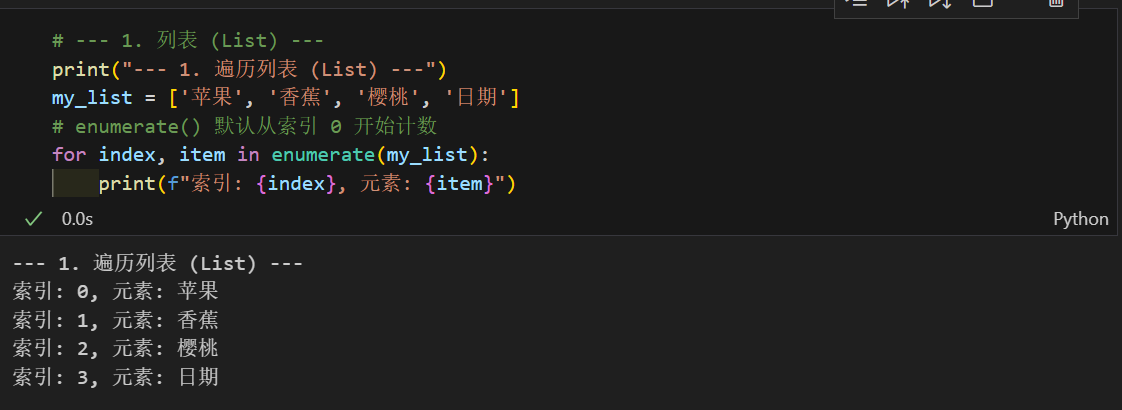
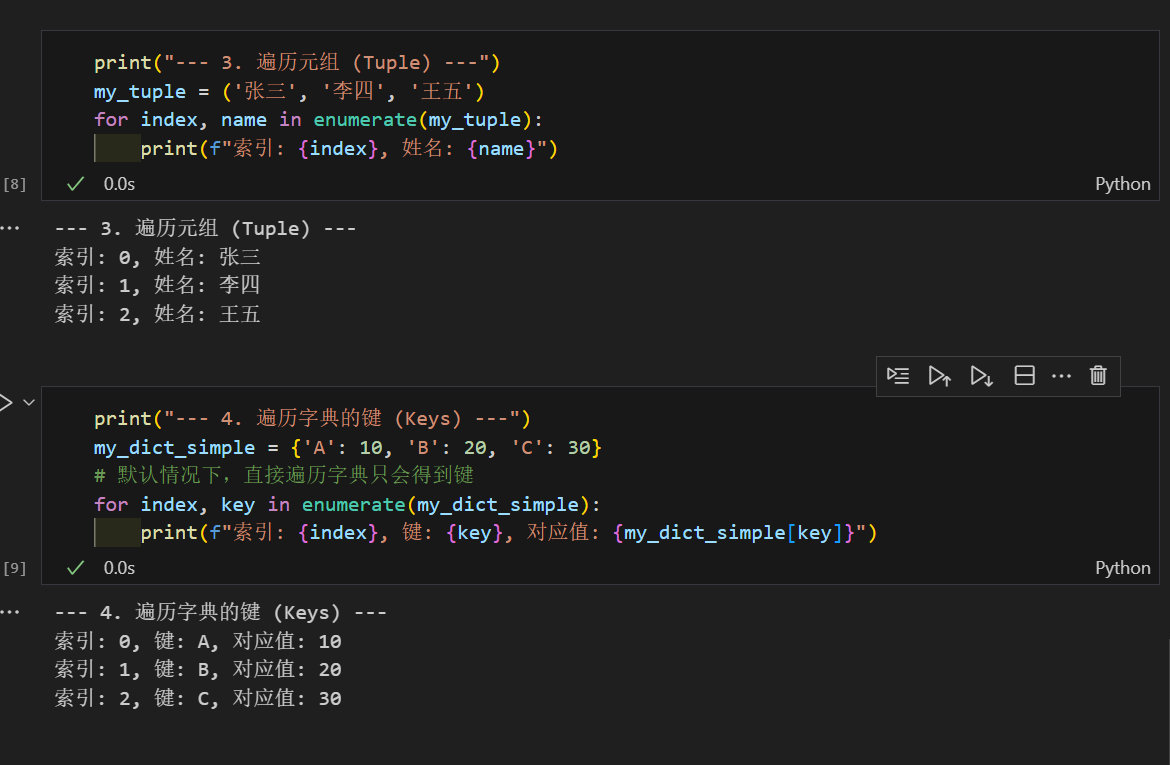
在python历史中，字典是无序的，Python 3.7 及更高版本，字典正式成为有序的。这意味着字典会记住键的插入顺序，并且在遍历时（包括使用 enumerate() 时），会严格按照这个顺序进行。这也意味着以后常见数据结构只能遇到集合是无序的了。

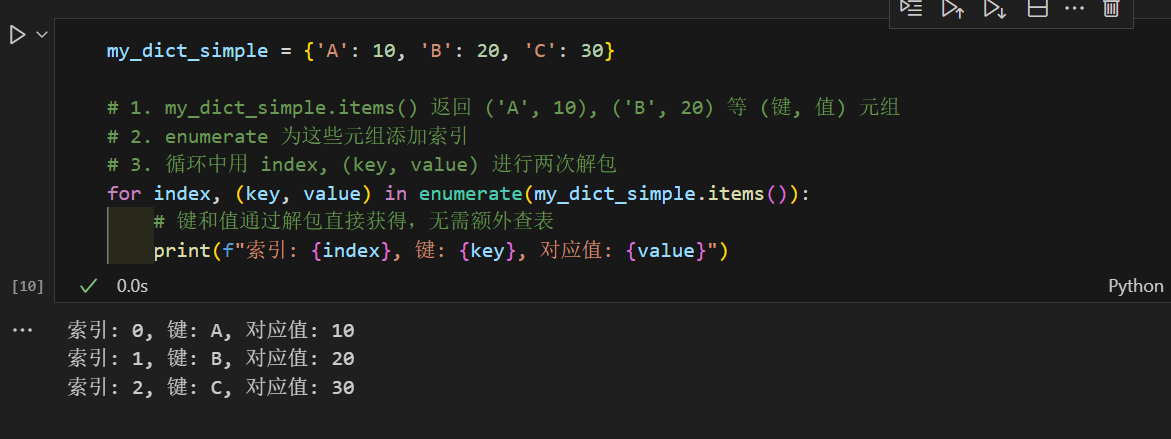
实际上下面这items和enumerate联合的写法非常常见

三、贝叶斯优化可视化

1. 数据准备

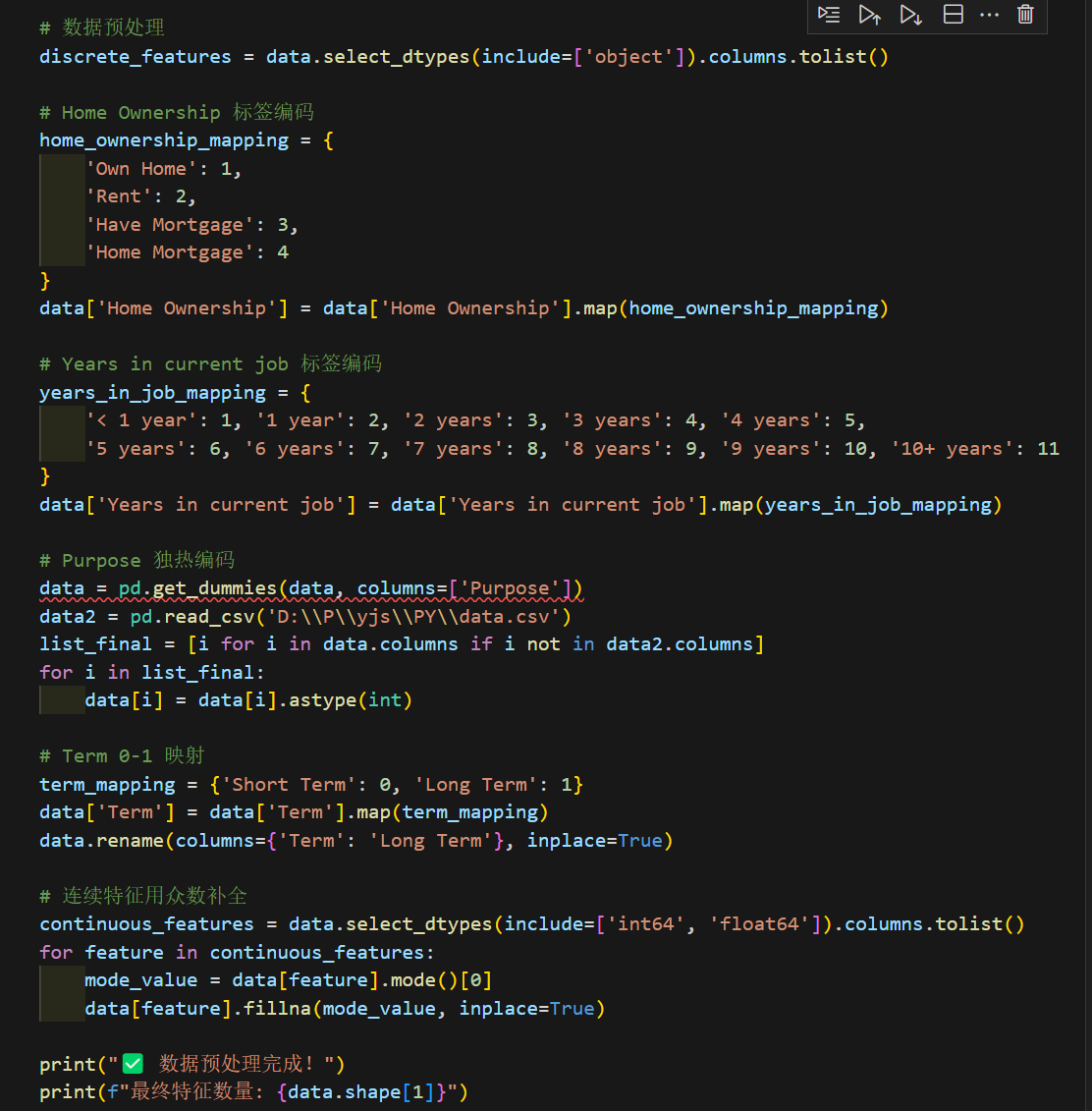
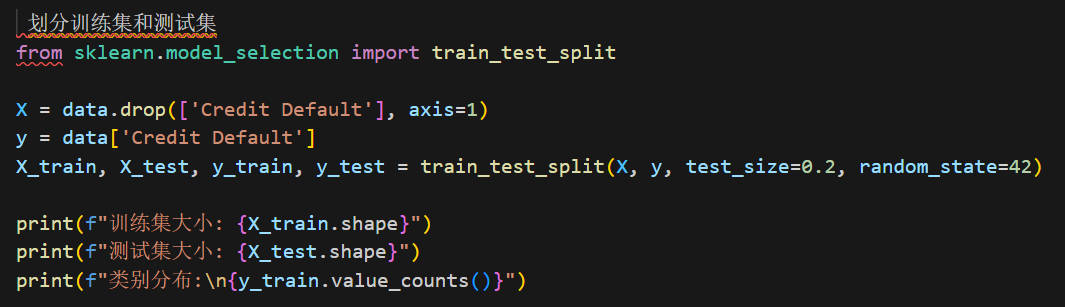
2. 基础贝叶斯优化

首先安装必要的库（如果还未安装）

我们今天选择贝叶斯优化库，他的自由度大很多。

from bayes_opt import BayesianOptimization
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.metrics import classification_report, confusion_matrix
import time

# 定义目标函数
def rf_eval(n_estimators, max_depth, min_samples_split, min_samples_leaf, max_features):
    """
    目标函数：评估随机森林在给定参数下的性能
    BayesianOptimization 会最大化这个函数的返回值
    
    参数说明：
    - n_estimators: 树的数量（越多越好，但会增加计算时间）
    - max_depth: 树的最大深度（太浅欠拟合，太深过拟合）
    - min_samples_split: 分裂所需最小样本数（控制树的生长）
    - min_samples_leaf: 叶节点最小样本数（防止过拟合）
    - max_features: 特征采样比例（增加随机性，防止过拟合）
    """
    # 将连续参数转换为整数
    n_estimators = int(n_estimators)
    max_depth = int(max_depth)
    min_samples_split = int(min_samples_split)
    min_samples_leaf = int(min_samples_leaf)
    # max_features 保持浮点数
    
    # 创建模型
    model = RandomForestClassifier(
        n_estimators=n_estimators,
        max_depth=max_depth,
        min_samples_split=min_samples_split,
        min_samples_leaf=min_samples_leaf,
        max_features=max_features,  
        random_state=42,
        n_jobs=-1
    )
    
    # 5折交叉验证
    scores = cross_val_score(model, X_train, y_train, cv=5, scoring='accuracy')
    return np.mean(scores)

# 定义参数搜索空间（扩大10倍！超大搜索空间）
pbounds = {
    'n_estimators': (10, 3000),          # 从10到3000棵树
    'max_depth': (3, 500),               # 从3到500
    'min_samples_split': (2, 200),       # 从2到200
    'min_samples_leaf': (1, 100),        # 从1到100
    'max_features': (0.1, 1.0)           # 从10%到100%
}


for param, (low, high) in pbounds.items(): # items方法返回字典的键值对
    range_size = high - low
    print(f"  {param:20s}: [{low:7.1f}, {high:7.1f}]  (范围: {range_size:7.1f})")

3. 详细输出与迭代过程

# 创建贝叶斯优化器，优化的过程已经被这个对象封装了
optimizer = BayesianOptimization(
    f=rf_eval, # 目标函数
    pbounds=pbounds,   # 参数搜索空间
    random_state=42,
    verbose=2  # 2: 详细信息, 1: 简要信息, 0: 不显示
)

start_time = time.time()

# 开始优化（大幅增加迭代次数以充分探索超大空间）
optimizer.maximize(
    init_points=20,  # 初始随机探索点数（增加到20以覆盖超大空间）
    n_iter=80        # 贝叶斯优化迭代次数（增加到80）
)

end_time = time.time()
print(f"优化完成！总耗时: {end_time - start_time:.2f} 秒".center(80))

4. 可视化优化过程 

 提取所有迭代的结果
iterations = []
scores = []
for i, res in enumerate(optimizer.res): # res包含每次迭代的结果，index从0开始
    iterations.append(i + 1) # 迭代次数从1开始
    scores.append(res['target']) # 提取得分

# 计算累计最优值
best_scores = []
current_best = -np.inf # 初始化为负无穷大
for score in scores: 
    if score > current_best: # 检查当前得分是否打破历史记录
        current_best = score
    best_scores.append(current_best)

# 绘制优化轨迹
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 5)) # 创建1行2列的子图

# 左图：每次迭代的得分
ax1.plot(iterations, scores, 'o-', label='每次迭代得分', alpha=0.7, markersize=6)
ax1.plot(iterations, best_scores, 'r--', label='累计最优得分', linewidth=2)
ax1.axhline(y=optimizer.max['target'], color='green', linestyle=':', 
            label=f'最终最优: {optimizer.max["target"]:.4f}') # axhline绘制水平线
ax1.set_xlabel('迭代次数', fontsize=12)
ax1.set_ylabel('准确率', fontsize=12)
ax1.set_title('贝叶斯优化收敛曲线 (超大空间100次迭代)', fontsize=14, fontweight='bold')
ax1.legend()
ax1.grid(True, alpha=0.3)

# 右图：初始探索 vs 贝叶斯优化
init_points = 20  # 更新为20
ax2.plot(iterations[:init_points], scores[:init_points], 'bo-', 
         label=f'随机探索 (前{init_points}次)', markersize=8, alpha=0.7)
ax2.plot(iterations[init_points:], scores[init_points:], 'go-', 
         label=f'贝叶斯优化 (后{len(iterations)-init_points}次)', markersize=8, alpha=0.7)
ax2.axvline(x=init_points, color='red', linestyle='--', alpha=0.5, label='探索→利用') # axvline绘制垂直线
ax2.set_xlabel('迭代次数', fontsize=12)
ax2.set_ylabel('准确率', fontsize=12)
ax2.set_title('探索阶段 vs 利用阶段', fontsize=14, fontweight='bold')
ax2.legend()
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 输出统计信息
print(f"  总迭代次数: {len(scores)}")
print(f"  最低得分: {min(scores):.4f}")
print(f"  最高得分: {max(scores):.4f}")
print(f"  平均得分: {np.mean(scores):.4f}")
print(f"  得分标准差: {np.std(scores):.4f}")
print(f"  得分提升: {max(scores) - scores[0]:.4f}")