python训练营打卡DAY9

@浙大疏锦行

知识点：

1. 相关系数热力图的绘制与解读
2. 子图布局的创建与使用
3. enumerate()函数的实用技巧

学习目标: 掌握多变量关系的可视化方法,学会使用子图进行批量绘图。

一、数据预处理回顾

在进行可视化分析之前,我们需要先完成数据的基本清洗和转换工作。

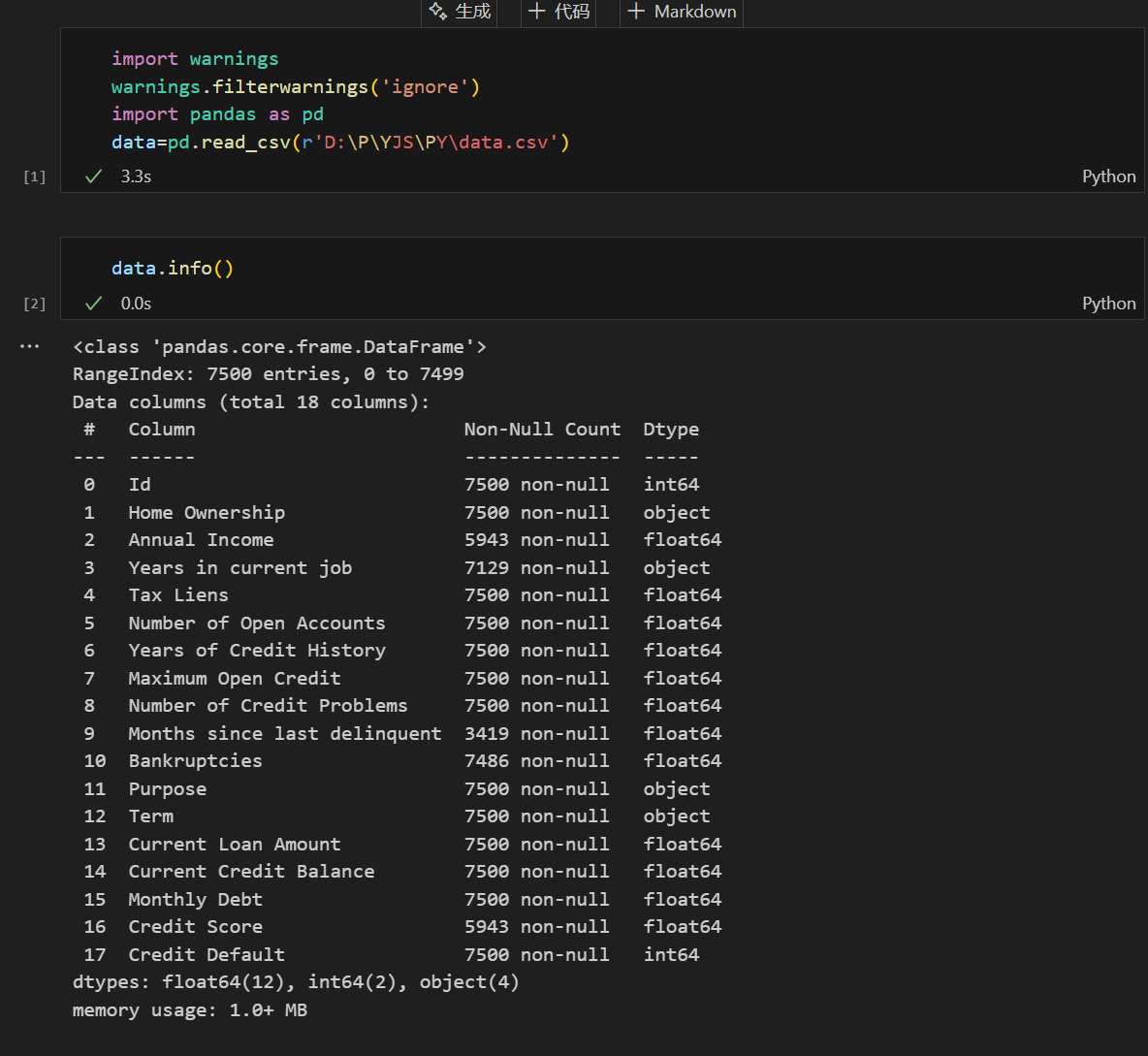
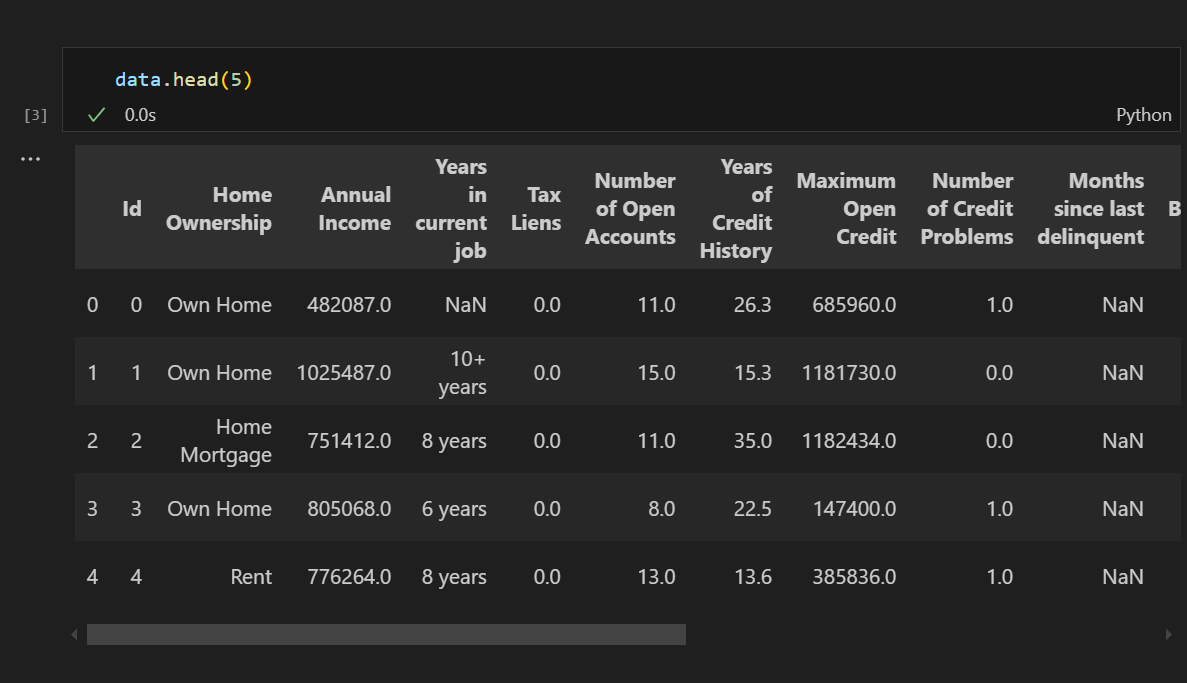
1.1 特征映射准备

对于包含字符串的分类特征,需要先转换为数值型才能进行后续的相关性分析。

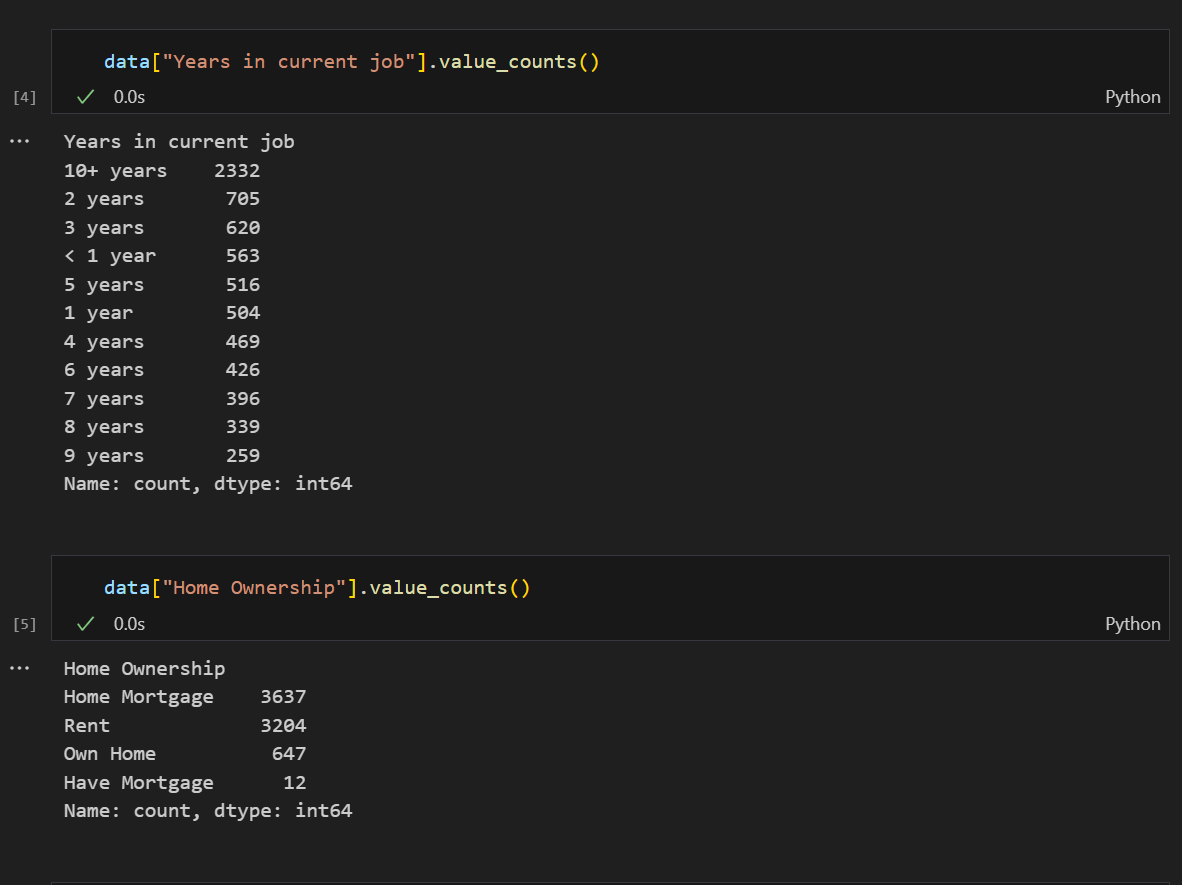
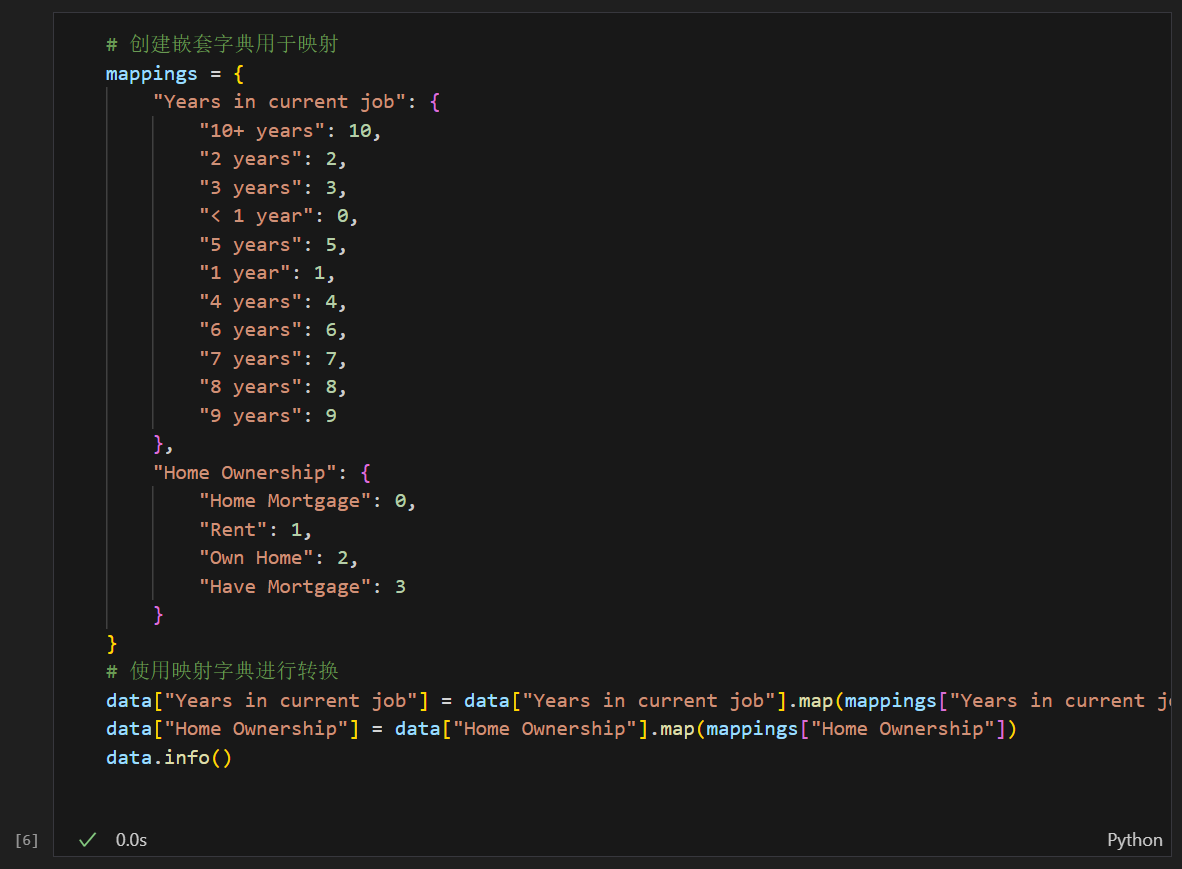
1.2 使用嵌套字典进行特征映射

为什么使用嵌套字典?

• 集中管理多个特征的映射规则
• 代码结构清晰,易于维护
• 方便批量处理多个特征

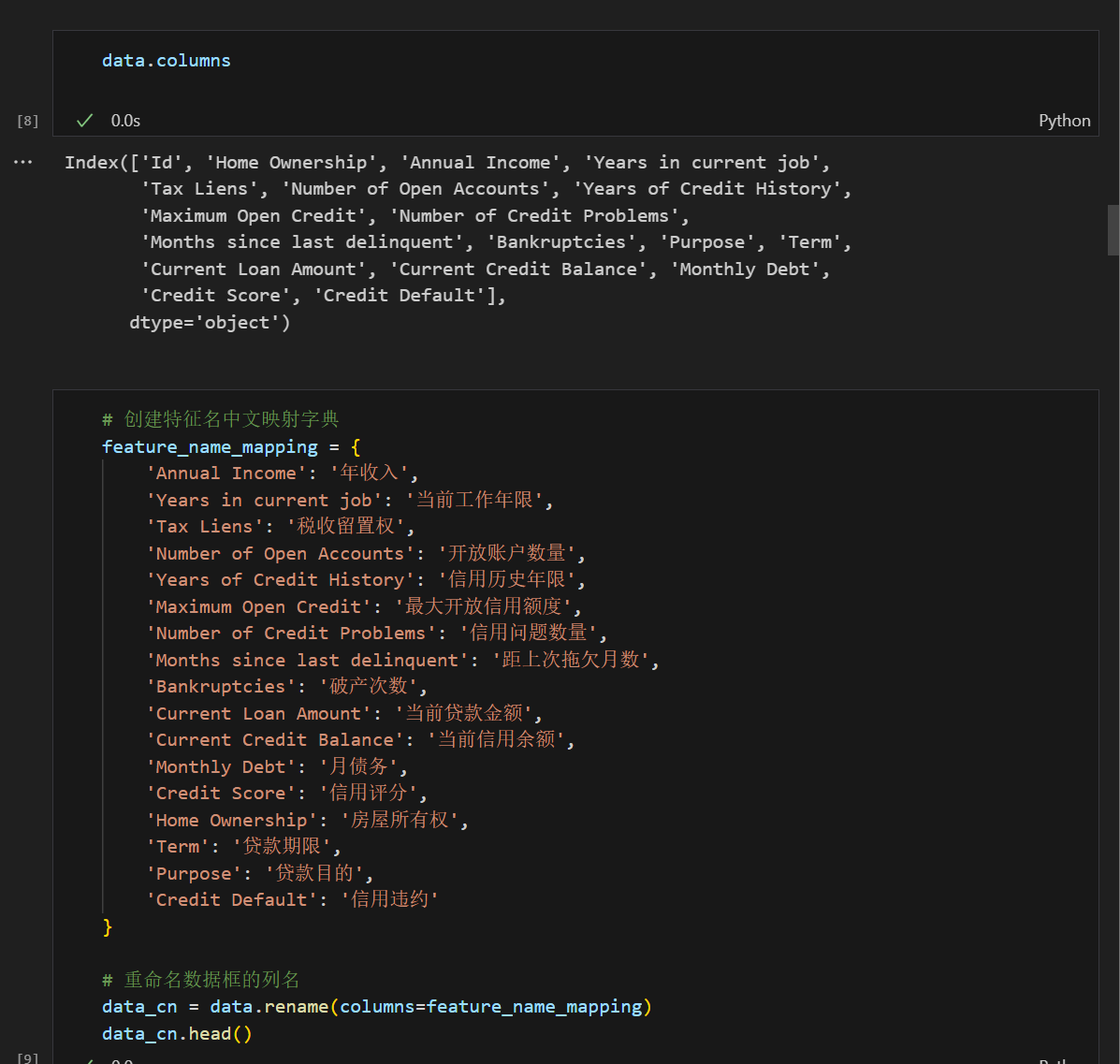
1.3 特征名中文映射

为了更好地理解数据,我们将英文特征名映射为中文特征名。

为什么需要中文映射?

• 提高可读性,更容易理解特征含义
• 方便团队沟通和报告展示
• 在热力图等可视化中展示更友好

二、相关系数热力图

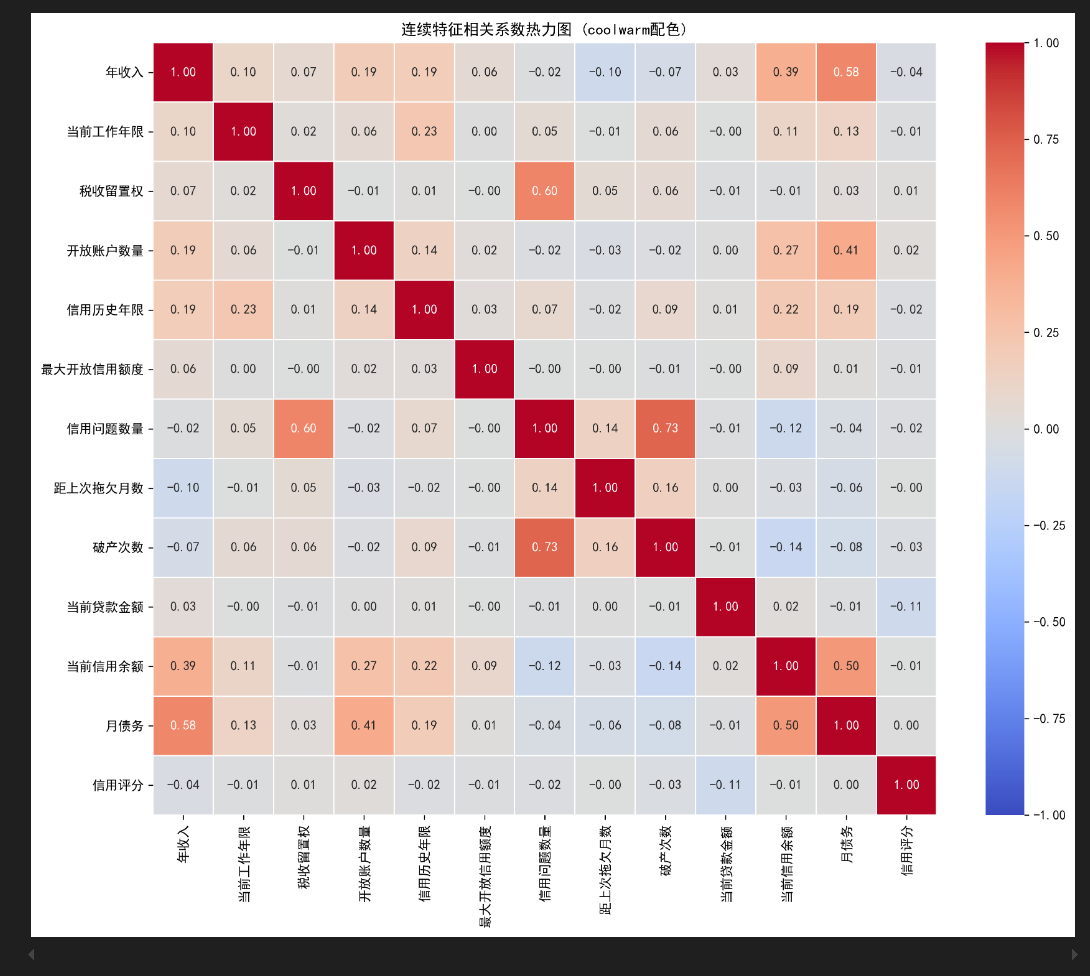
2.1 什么是相关系数热力图?

热力图(Heatmap)是一种通过颜色深浅来展示数据矩阵的可视化方法。在数据分析中,我们常用热力图来展示特征之间的相关系数矩阵。

相关系数的含义:

• 取值范围: [-1, 1]
• 接近1: 强正相关(一个增加,另一个也增加)
• 接近-1: 强负相关(一个增加,另一个减少)
• 接近0: 无线性相关关系

注意事项:

• 热力图适合展示连续变量之间的关系
• 对于离散变量,相关系数的意义需要谨慎解读
• 本例中为了演示方便,对所有数值型特征都进行了计算

皮尔逊相关系数（Pearson Correlation Coefficient），通常用符号 r 表示，是衡量两个连续变量（例如 X 和 Y）之间线性关系强度和方向的指标。

以下是它的公式：

📈 皮尔逊相关系数公式

1. 协方差和标准差形式

这是最容易理解其统计意义的形式：

rX,Y=Cov(X,Y)σXσY

其中：

• Cov(X,Y) 是 X 和 Y 的协方差。
• σX 是 X 的标准差。
• σY 是 Y 的标准差。

这个公式本质上就是标准化（除以标准差）后的协方差。

---

2. 计算公式（样本）

这是在实际计算中更常用的展开形式：

r=∑i=1n(xi−x¯)(yi−y¯)∑i=1n(xi−x¯)2∑i=1n(yi−y¯)2

其中：

• n 是样本点的数量。
• xi 和 yi 是第 i 个样本的观测值。
• x¯ 是 X 的平均值（均值）。
• y¯ 是 Y 的平均值（均值）。

🔢 系数解读

皮尔逊相关系数 r 的取值范围是 [−1,1]：

• r=1： 完美的正线性相关（X 增大，Y 也增大）。
• r=−1： 完美的负线性相关（X 增大，Y 反而减小）。
• r=0： 几乎没有线性相关关系。

简而言之，它告诉你两件事：方向（正相关还是负相关）和力量（相关程度有多强）。

您想让我提供一个简单的数值例子，来演示如何使用这个公式计算相关系数吗？

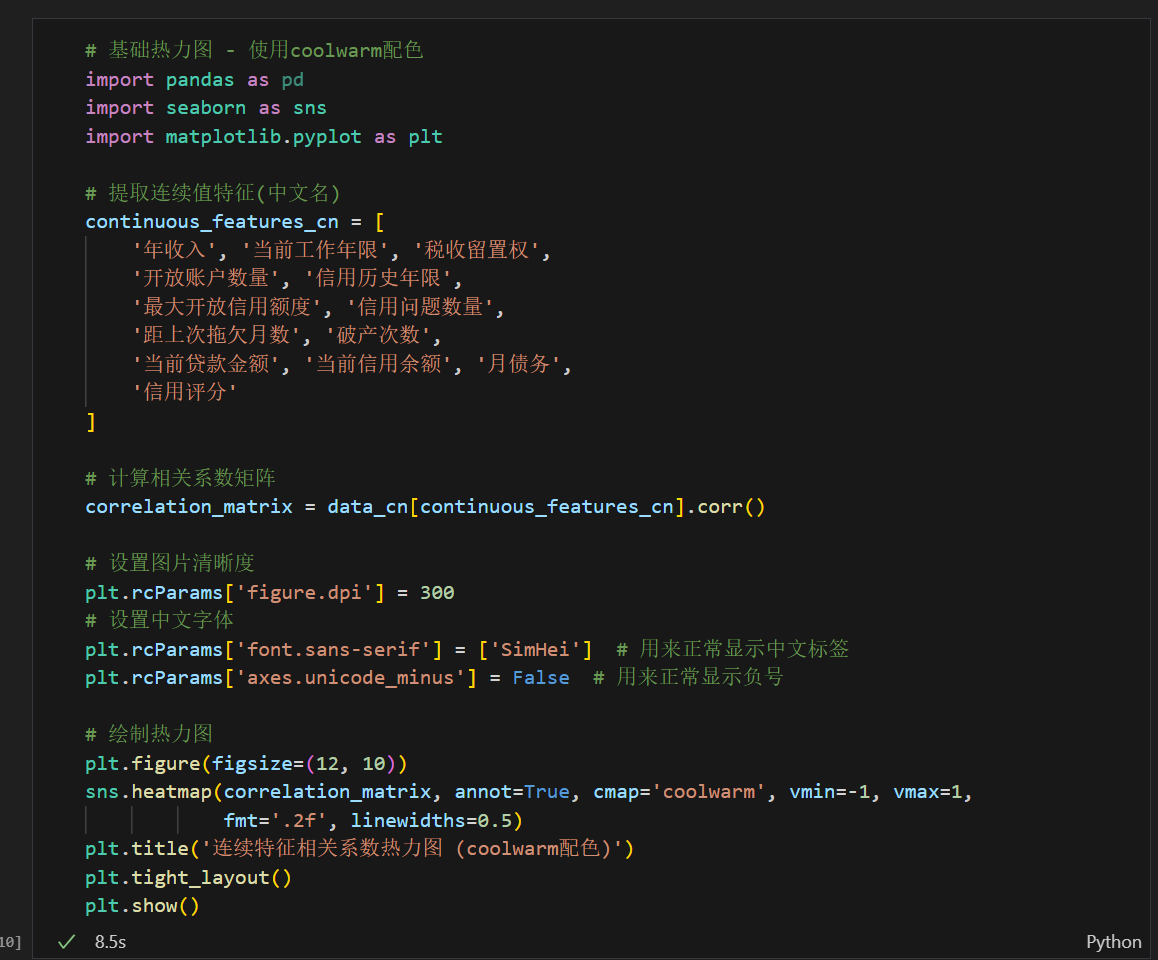
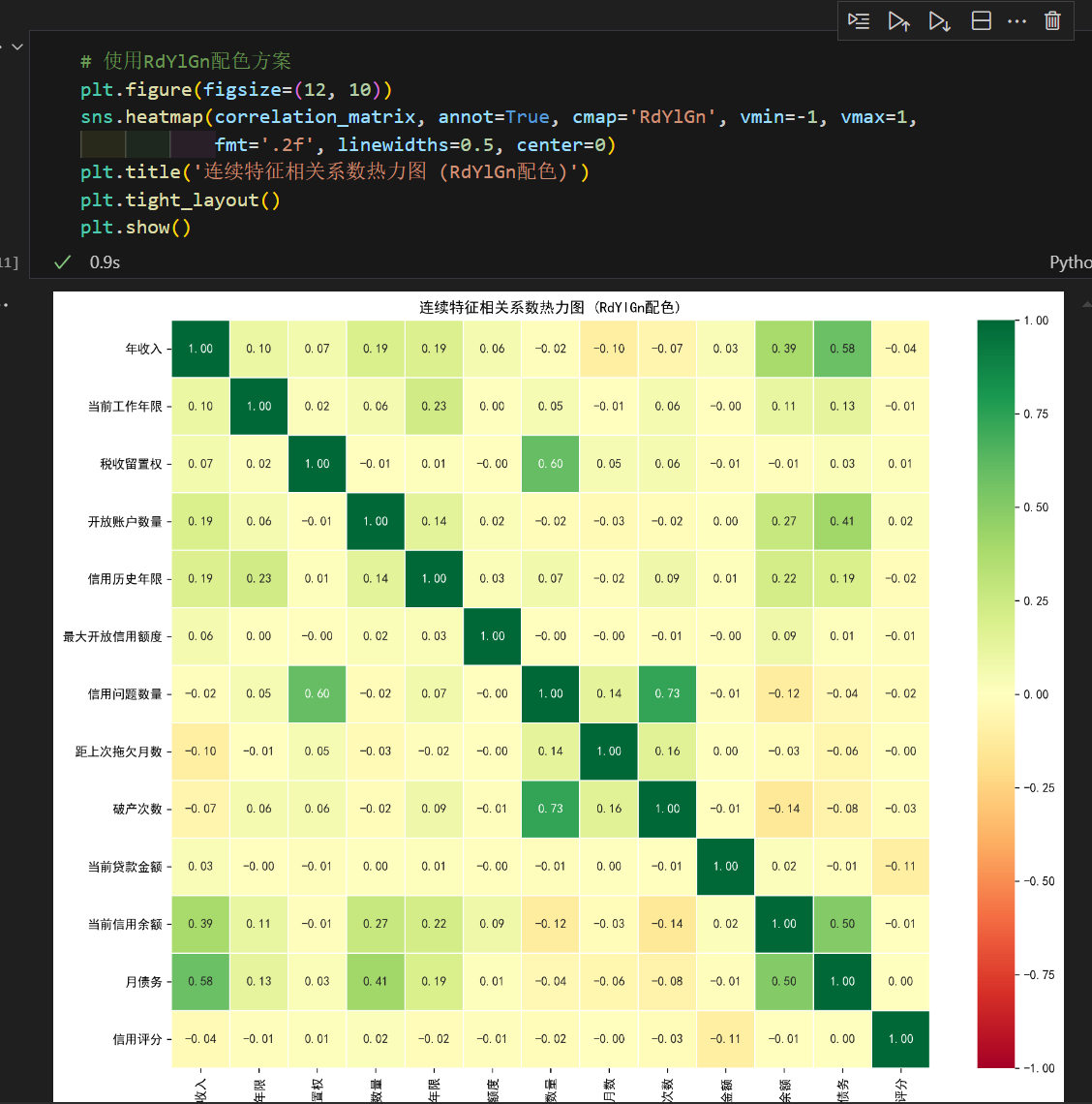
2.2 不同配色方案的热力图

不同的配色方案适用于不同的场景,下面展示几种常用的配色方案。

常用配色方案:

• coolwarm: 冷暖色调,适合展示正负相关(蓝色表示负相关,红色表示正相关)
• RdYlGn: 红黄绿配色,直观展示好坏程度
• viridis: 色盲友好,从紫色到黄色的渐变
• plasma: 鲜艳的紫红黄配色
• YlOrRd: 从黄色到橙色到红色,适合展示强度

.3 热力图参数说明

主要参数解释:

• annot=True: 在每个单元格中显示数值
• cmap: 配色方案
• vmin, vmax: 设置颜色条的最小值和最大值
• fmt='.2f': 数值格式,保留2位小数
• linewidths: 单元格之间的线宽
• center: 设置颜色的中心值(通常设为0)
• square=True: 设置单元格为正方形
• cbar_kws: 颜色条的参数设置

三、子图绘制

3.1 什么是子图?

子图(Subplot)是指在一个图表窗口中同时显示多个独立的图表。通过子图布局,我们可以:

• 在一张图中展示多个变量的分布
• 方便对比不同特征的特征
• 节省空间,提高可视化效率

常用方法:

• plt.subplots(): 创建子图网格
• enumerate(): 遍历列表时同时获取索引和值

import numpy as np
import matplotlib.pyplot as plt


# -----------------
# 1. 创建模拟数据
# -----------------
# 子图A的数据：正弦波
X_sin = np.linspace(0, 2 * np.pi, 100)
Y_sin = np.sin(X_sin)

# 子图B的数据：随机散点
X_scatter = np.random.rand(50)
Y_scatter = np.random.rand(50)

# 子图C的数据：条形图
categories = ['A', 'B', 'C', 'D']
values = [15, 30, 10, 25]

# 子图D的数据：线性衰减
X_linear = np.arange(10)
Y_linear = 10 - X_linear * 0.8 + np.random.randn(10) * 0.5


# -----------------
# 2. 绘制子图（核心步骤）
# -----------------

# 使用 plt.subplots() 创建 2x2 的子图布局
# fig: 代表整个画布（Figure）
# axes: 是一个包含所有子图坐标轴对象的 NumPy 数组
fig, axes = plt.subplots(
    nrows=2,           # 行数 (Number of Rows)
    ncols=2,           # 列数 (Number of Columns)
    figsize=(10, 8),   # 整个画布的大小 (10英寸宽, 8英寸高)
    dpi=100            # 分辨率，确保清晰度
)

# -----------------
# 3. 分别在每个子图上绘图和设置属性
# -----------------

# 子图 A (位于第一行第一列：axes[0, 0]) - 绘制折线图
ax_A = axes[0, 0]
ax_A.plot(X_sin, Y_sin, color='tab:blue', label='Sin Wave')
ax_A.set_title('(a) 正弦波变化', fontsize=14, fontweight='bold')
ax_A.set_xlabel('时间 (t)')
ax_A.set_ylabel('振幅 (A)')
ax_A.legend()

# 子图 B (位于第一行第二列：axes[0, 1]) - 绘制散点图
ax_B = axes[0, 1]
ax_B.scatter(X_scatter, Y_scatter, c=X_scatter, cmap='viridis', alpha=0.7)
ax_B.set_title('(b) 随机散点分布', fontsize=14, fontweight='bold')
ax_B.set_xlabel('特征 X')
ax_B.set_ylabel('特征 Y')

# 子图 C (位于第二行第一列：axes[1, 0]) - 绘制条形图
ax_C = axes[1, 0]
ax_C.bar(categories, values, color='tab:orange')
ax_C.set_title('(c) 分类计数', fontsize=14, fontweight='bold')
ax_C.set_xlabel('类别')
ax_C.set_ylabel('数量')

# 子图 D (位于第二行第二列：axes[1, 1]) - 绘制带误差的折线图
ax_D = axes[1, 1]
ax_D.errorbar(X_linear, Y_linear, yerr=0.5, fmt='-o', color='tab:red', capsize=4)
ax_D.set_title('(d) 线性衰减趋势', fontsize=14, fontweight='bold')
ax_D.set_xlabel('迭代次数')
ax_D.set_ylabel('结果值')


# -----------------
# 4. 调整整体布局
# -----------------

# 自动调整子图参数，使之填充整个 figure 区域，避免标签重叠
fig.tight_layout(pad=3.0) 

# 给整个画布添加一个总标题
fig.suptitle('论文多子图绘制示例', fontsize=18, fontweight='bold', y=1.02)


# -----------------
# 5. 显示和保存
# -----------------
plt.show()

# 如果要保存高质量图片，建议使用矢量格式，例如：
# fig.savefig('my_subplots.pdf', format='pdf', bbox_inches='tight') 
# fig.savefig('my_subplots.png', dpi=300) # 位图保存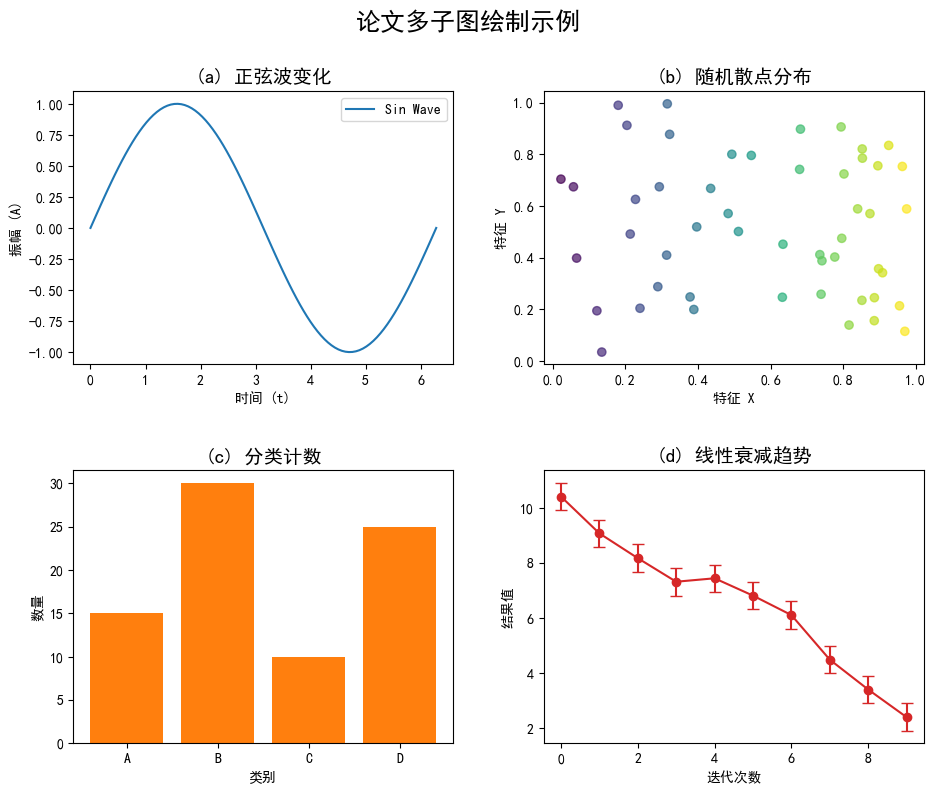

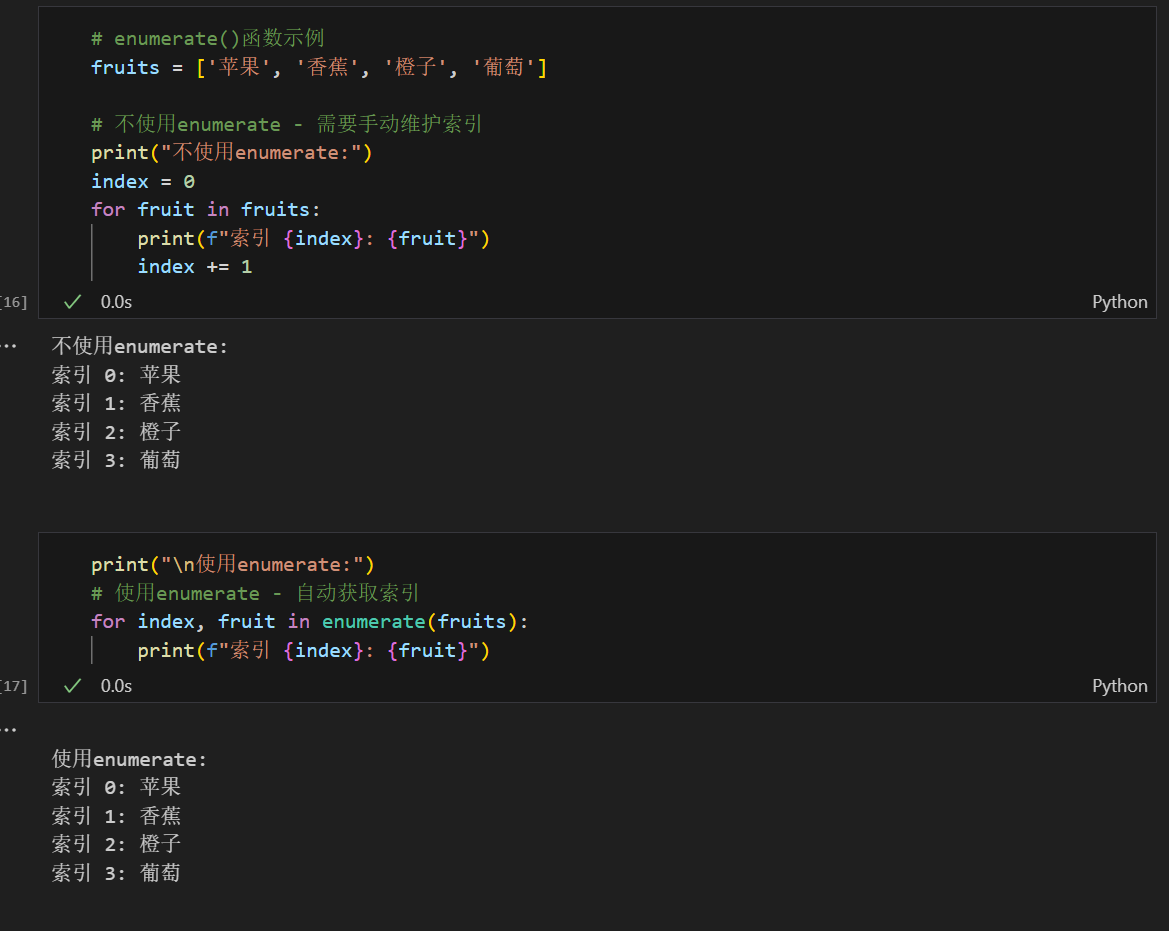
3.2 enumerate()函数介绍

在遍历列表时,我们经常需要同时获取元素的索引和值。enumerate()函数可以优雅地实现这个需求。

基本用法:

for index, value in enumerate(list):
    # index是索引,value是值

为什么需要索引?

• 在子图绘制中,需要用索引来定位每个子图的位置
• 可以根据索引进行条件判断或特殊处理

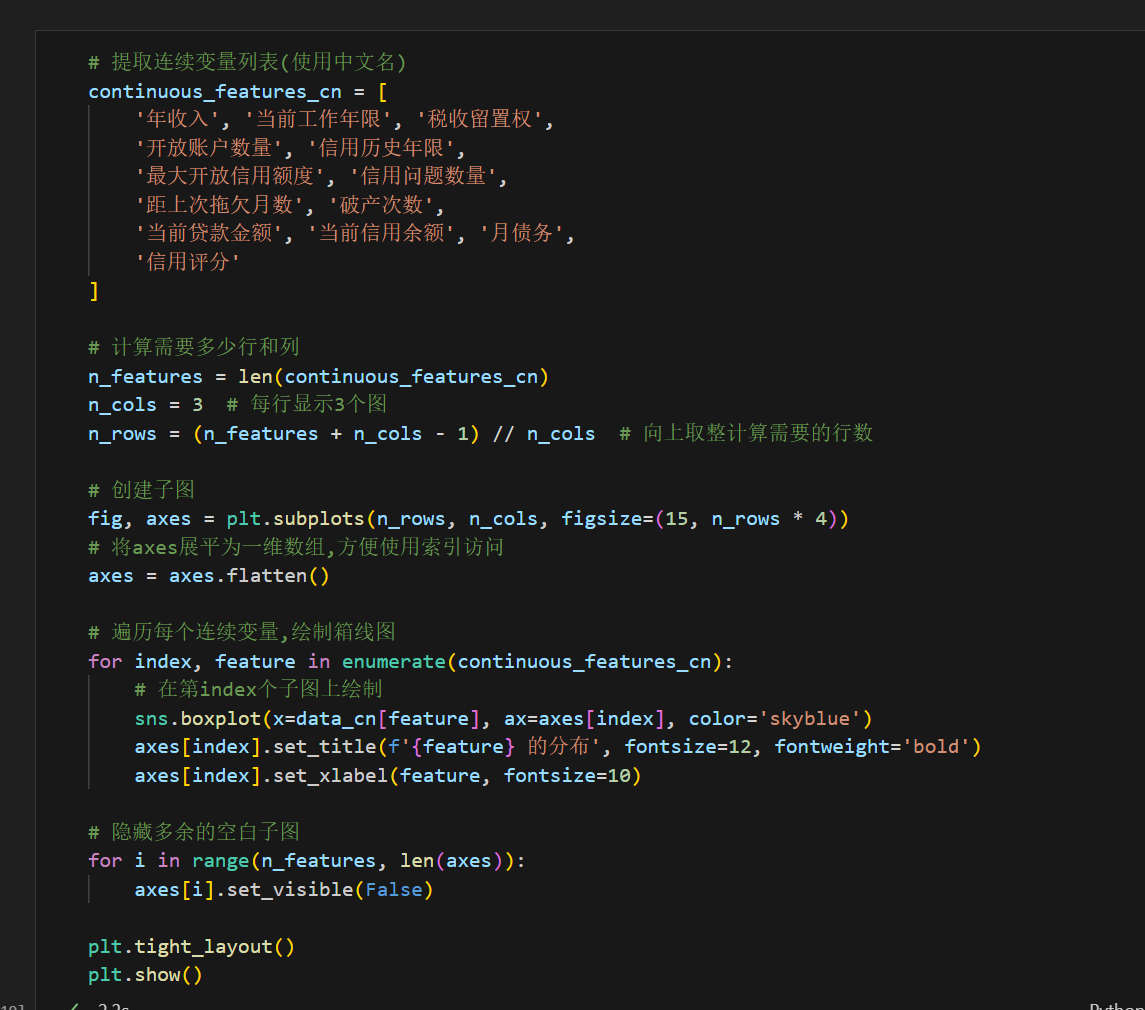
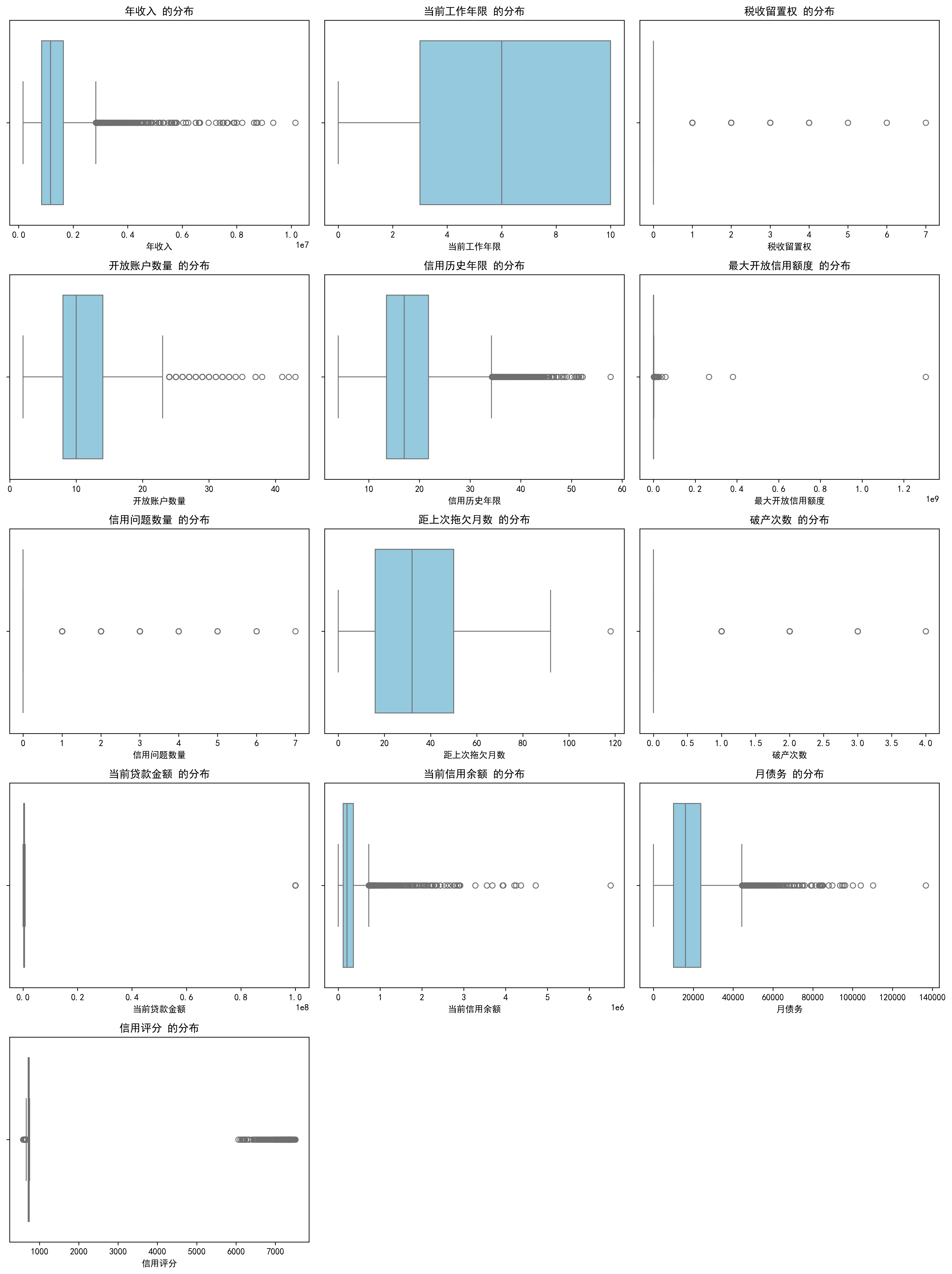
3.3 批量绘制连续变量箱线图

现在我们使用子图来批量绘制所有连续变量的箱线图,观察每个特征的分布特征。

箱线图的作用:

• 展示数据的中位数、四分位数
• 识别异常值(outliers)
• 了解数据的分散程度

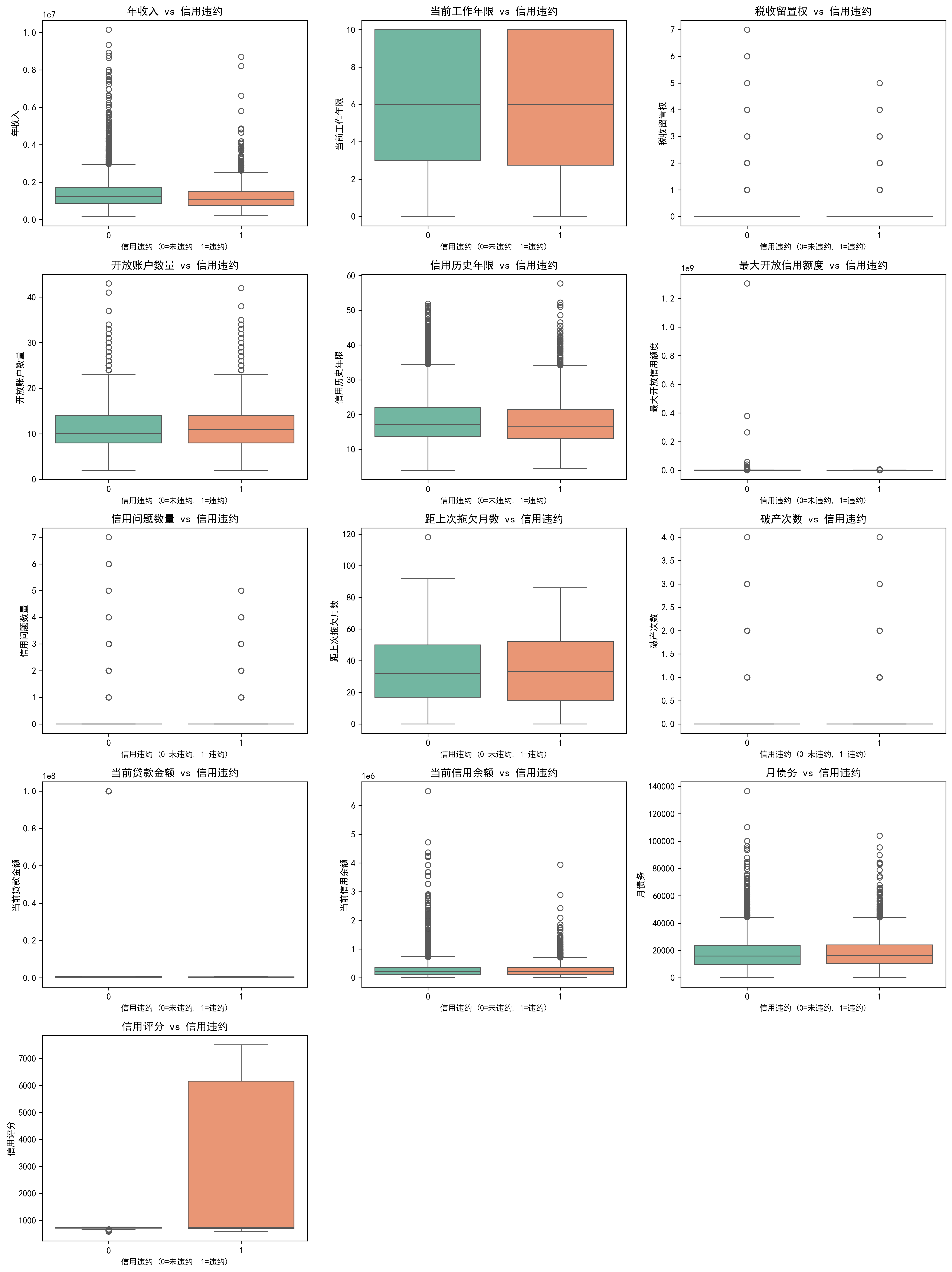
3.4 按信用违约分组的箱线图

我们还可以进一步细化,按照信用违约状态来分组显示每个特征的分布,这样可以更好地观察特征与目标变量的关系。

3.5 代码解析

关键代码说明:

1. 计算子图布局:

   n_cols = 3  # 每行3列
   n_rows = (n_features + n_cols - 1) // n_cols  # 向上取整
   

2. 创建子图网格:

   fig, axes = plt.subplots(n_rows, n_cols, figsize=(15, n_rows * 4))
   axes = axes.flatten()  # 转为一维数组
   

3. 使用enumerate遍历:

   for index, feature in enumerate(continuous_features_cn):
       sns.boxplot(..., ax=axes[index])  # 使用索引定位子图
   

4. 隐藏多余子图:

   for i in range(n_features, len(axes)):
       axes[i].set_visible(False)